Magiked Square
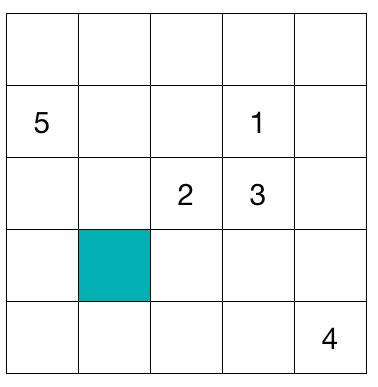
In the 5 × 5 grid, each square contains the number 1, 2, 3, 4 or 5 such that no row, column or main diagonal contains the same number more than once.
What is the value of the blue square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I didn't realize that it was so easy to see the blue square could only be a 4. I had a much longer elimination process.
Log in to reply
I got to this solution the long way. I was only focusing on the rows and columns at first and had nearly finished filling in the whole square when I finally realized that the diagonal was the key, at least in this case. This is a fun type of puzzle; I guess it can vary in difficulty by changing the initial information provided.
Log in to reply
I love this, am really amazed. That describes what I did!
I thought this was going to involve a lot of logical deductions, and was surprised to see your solution. That's because I only considered my own way of solving this problem, and selected one of the last few squares that I could fill in. I didn't then "re-solve" the problem and see if there is a nice approach.
I am trying my hand at creating these puzzles, given the popularity of Sudoku.
Log in to reply
@Chung Kevin – Looking forward to trying any new creations. :)
I got an answer... 3 4 2 5 1, 5 2 4 1 3, 4 1 5 3 2, 2 3 1 4 5, 1 5 3 2 4.
Log in to reply
from left to right...
Log in to reply
With that arrangement there are three 1's in one diagonal and two 4's in the other, contrary to the conditions of the problem.
i came up with this answer, where 5 is in the blue box 4 3 5 2 1, 5 2 4 1 3, 1 4 2 3 5, 3 5 1 4 2, 2 1 3 5 4
Log in to reply
The rows and columns of your solution satisfy the conditions of the question, but the main diagonals do not, as from left to right they go 4 , 2 , 2 , 4 , 4 and 2 , 5 , 2 , 1 , 1 .
Consider the main right diagonal , 1 , 2 are already there so the blue box may contain 4 or 3 or 5.
From the figure , we see that 4 is there in the rightmost corner at the bottom so 4 cannot be placed at the two ends of the diagonal(considering the rule to place it in a box) . And so the only place left for 4 is the blue box.
No need to solve the grid.
It is simply that if anything but 4 goes in the square, the 4 will be duplicated at either corner, and has no place else to go.
All the same here is a solved grid.
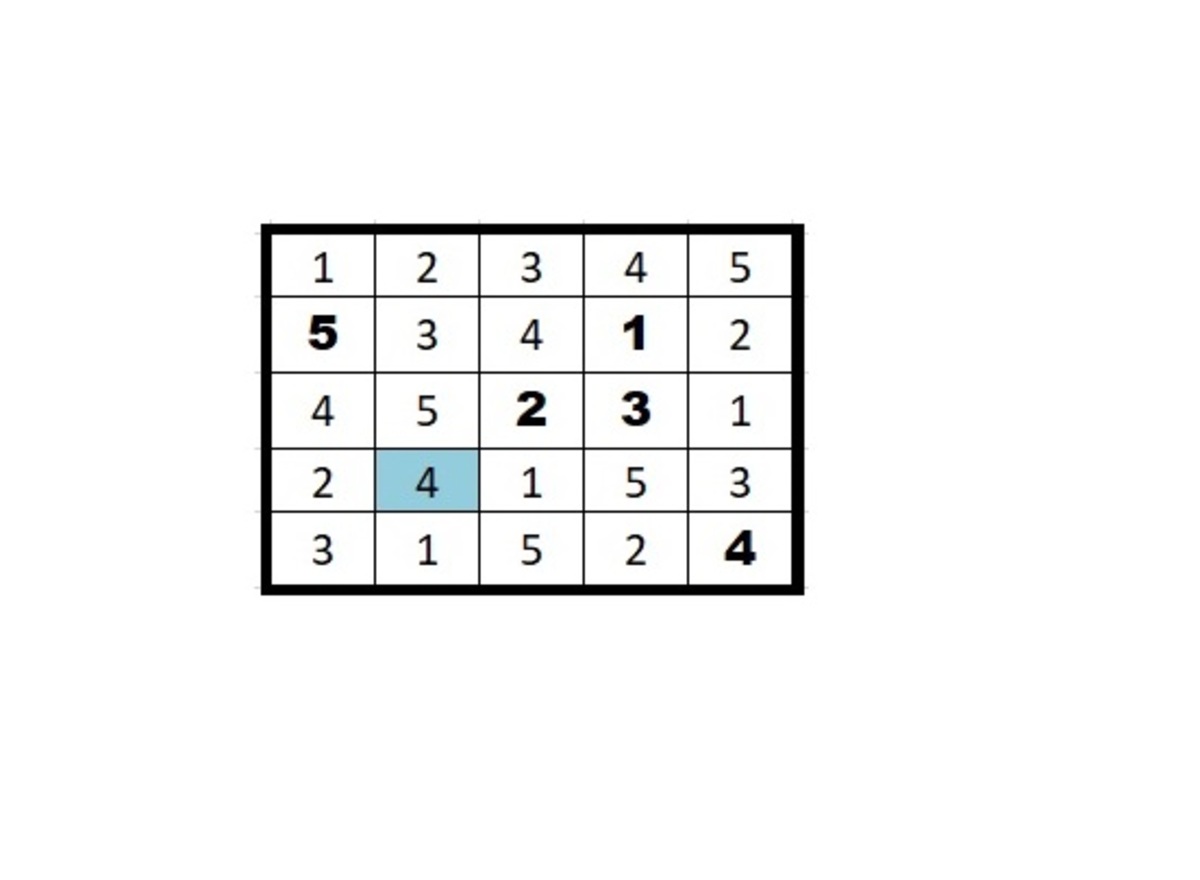
That's the unique way to fill up the square :) I was surprised that even though the information felt sparse, there was only this 1 approach.
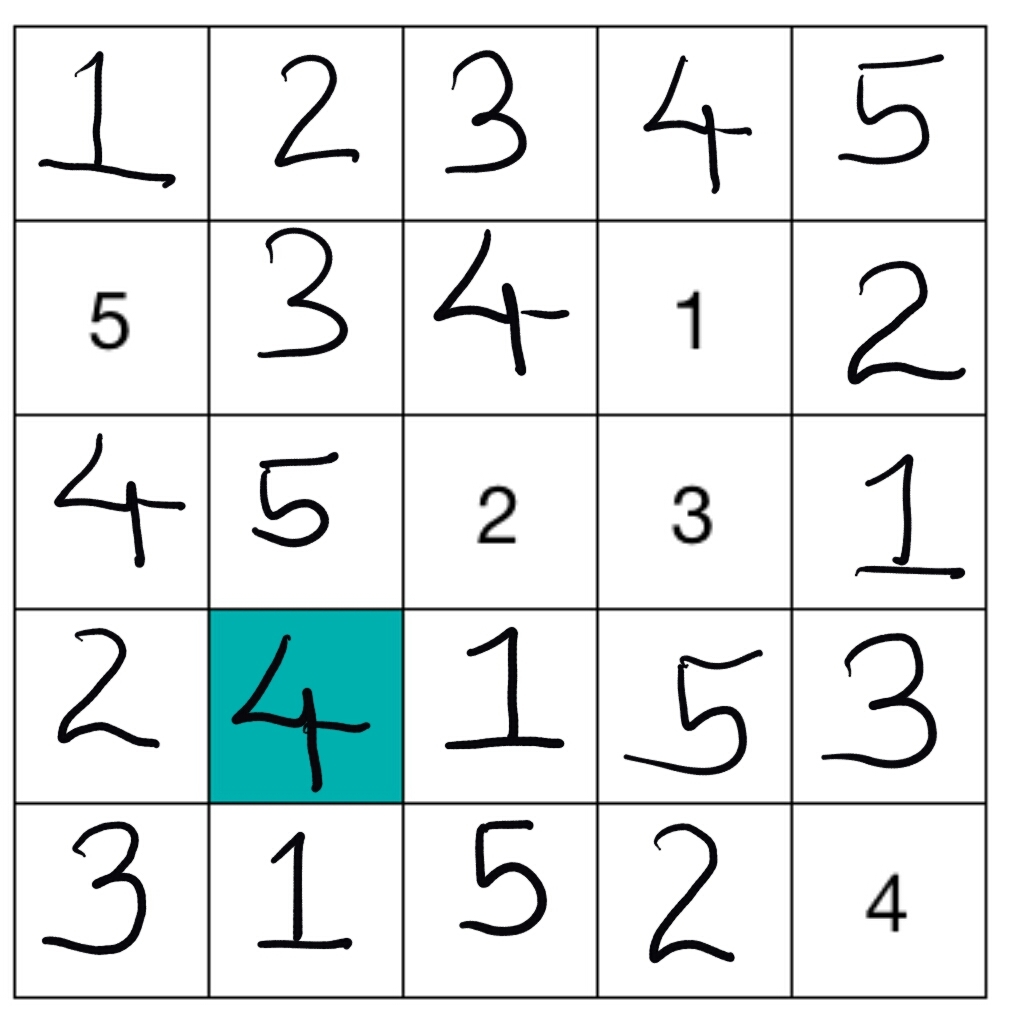
Looking at where to place the 4 in the diagonal going from the lower left to the upper right box, the 4 in the lower right box negates the possibility of putting a 4 in the lower left or upper right box. Since the 1 and 2 already take up two of the three remaining positions, there is only one place left to put the 4, namely in the blue box. To be complete, we now need to see if such a 5 x 5 grid can be completed. Indeed, it can, uniquely:
1 . . . 2 . . . 3 . . . 4 . . . 5
5 . . . 3 . . . 4 . . . 1 . . . 2
4 . . . 5 . . . 2 . . . 3 . . . 1
2 . . . 4 . . . 1 . . . 5 . . . 3
3 . . . 1 . . . 5 . . . 2 . . . 4
The answer is therefore 4 .