Ring and Magnetism (09-08-2020)
A uniform current carrying ring of mass
m
and radius
R
is connected by a massless string as shown.
A uniform magnetic field
B
0
exists in the region to keep the ring in the horizontal position.
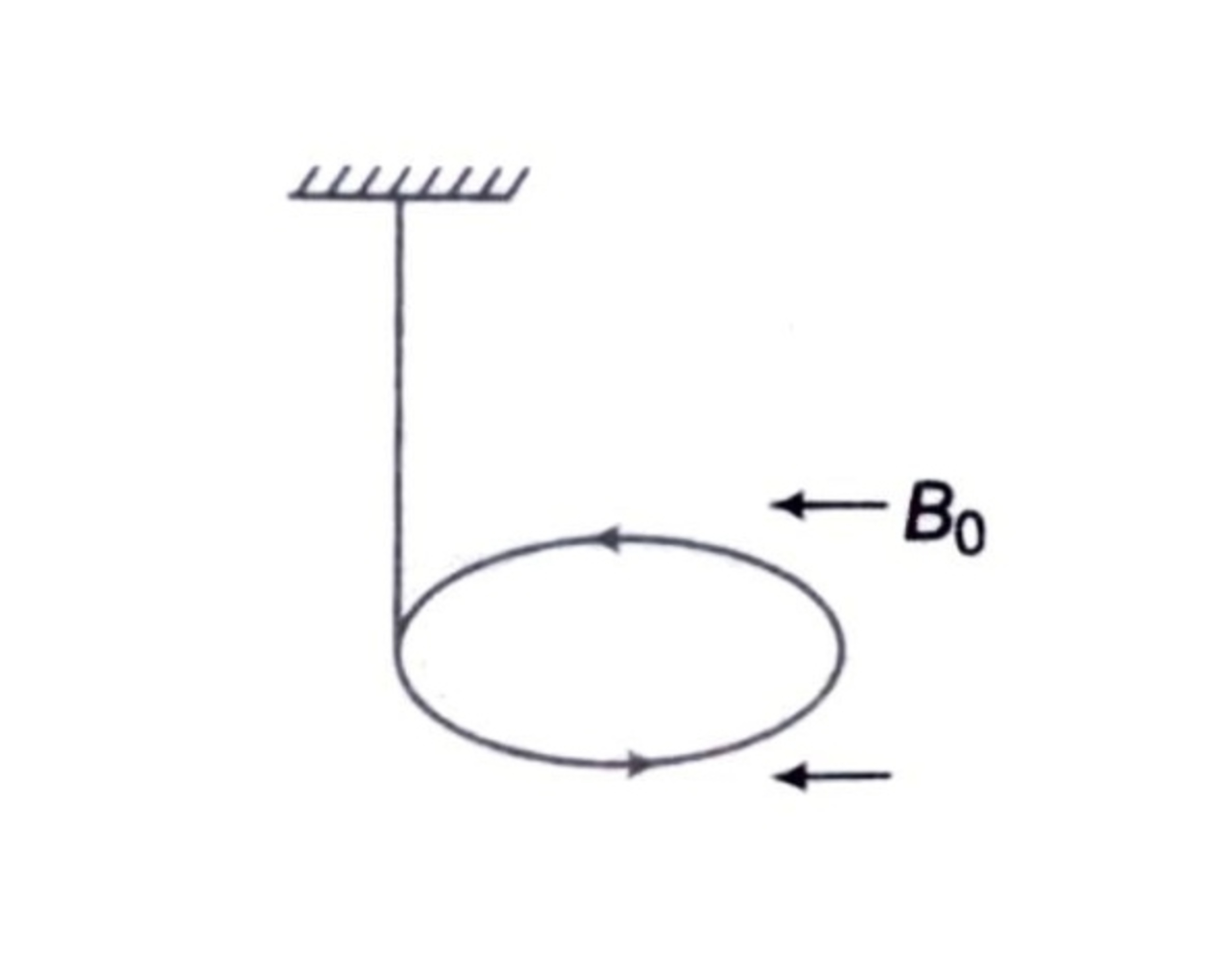 Then find the current in the ring.
Then find the current in the ring.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Steven Chase
Thanks for the solution. You are on fire.
I didn't understand that
r
in Torque equation.
r
=
(
R
c
o
s
θ
+
R
,
sin
θ
,
0
)
Log in to reply
It is the vector from the anchor point to a point on the ring
Log in to reply
@Steven Chase
How did you created that?
Except this I understood your whole solution.
Log in to reply
@Talulah Riley – r = ( R cos θ , R sin θ , 0 ) − ( − R , 0 , 0 )
Log in to reply
@Steven Chase – @Steven Chase why we have neglected that negative sign while equating the torque?
Log in to reply
@Talulah Riley – Because I know that one is positive and one is negative, so they will cancel with the appropriate current magnitude. All that is left is to find the magnitude of the current.
@Steven Chase
your analytical solutions seems me more explanatory than Karan sir.
Thanks
Log in to reply
You're welcome. My analytical solutions are similar to my code, in that I like to break things into little pieces.
The magnetic and gravitational torques about the anchor point should sum to zero. Let the anchor point be at ( x , y , z ) = ( − R , 0 , 0 ) . The path coordinates and infinitesimal displacement elements are:
x = R cos θ y = R sin θ z = 0 d x = − R sin θ d θ d y = R cos θ d θ d z = 0
The magnetic force on a piece of the curve is:
d F = I d ℓ × B d ℓ = ( d x , d y , d z ) = ( − R sin θ d θ , R cos θ d θ , 0 ) B = ( − B 0 , 0 , 0 )
Taking the cross product results in the following infinitesimal forces:
d F x = 0 d F y = 0 d F z = I B 0 d y = I B 0 R cos θ d θ
The infinitesimal magnetic torque is:
d τ = r × d F r = ( R cos θ + R , R sin θ , 0 )
Taking the cross product results in the following infinitesimal torques:
d τ x = I B 0 R 2 sin θ cos θ d θ d τ y = − I B 0 R 2 cos 2 θ d θ − I B 0 R 2 cos θ d θ d τ z = 0
Integrating these from θ = 0 to θ = 2 π results in:
τ x = 0 τ y = − π I B 0 R 2 τ z = 0
The gravitational torque is:
τ g = ( R , 0 , 0 ) × ( 0 , 0 , − m g ) = ( 0 , m g R , 0 )
Observe that these two torques can cancel if the current has the right magnitude.
π I B 0 R 2 = m g R I = π B 0 R m g