Magnetism Exercise

Electricity and Magnetism Level pending

A parabolic green wire has a resistance of ρ 1 \rho_1 per unit length. A blue straight ( x = 4 ) (x=4) a resistance of ρ 2 \rho_2 per unit length. Both the wires are in x y xy plane . Their ends are connected toa battery of V volts.
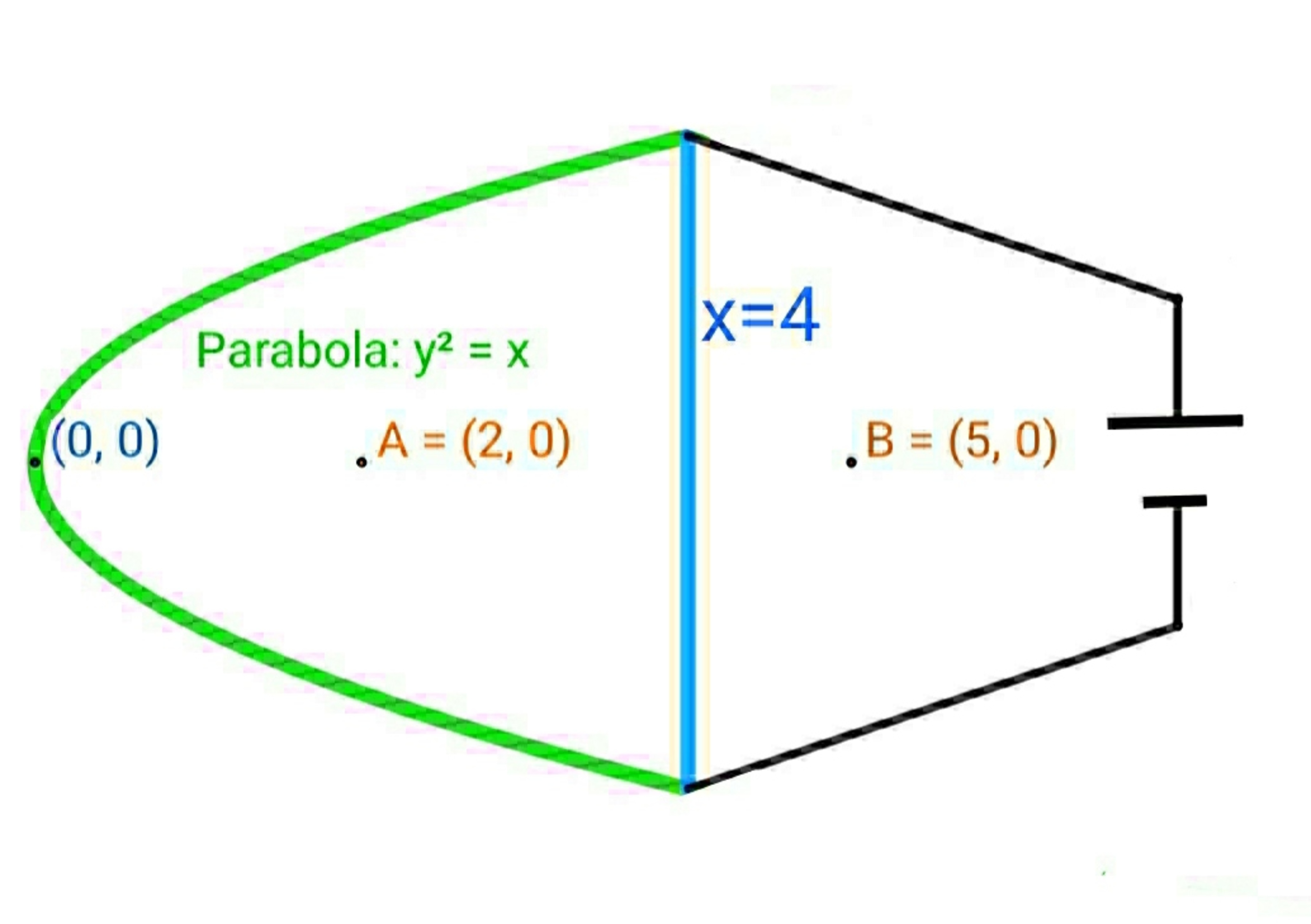
If the magnetic field at A A is B A B_A and at B B is B B B_B
Type your answer as B B B A \frac{B_B}{B_A}

Details and Assumption
1) Neglect the contribution of magnetic field through black wire.
2) Black wire have 0 0 resistance and the battery used in the circuit have 0 0 internal resistance.
3) ρ 1 = 2 , ρ 2 = 1 , v = 10 \rho_1=2,\rho_2=1,v=10
4) Consider everything in SI units.

The problem is original.


The answer is -27.678.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Steven Chase
May 29, 2020

Simulation code attached. At point A, the fields largely cancel, and at point B, the fields reinforce each other. So the magnitude at B is much larger than at A. 

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
 
import math

# Constants

dy = -(10.0**(-6.0))

p1 = 2.0
p2 = 1.0
V = 10.0

xA = 2.0
yA = 0.0

xB = 5.0
yB = 0.0

#######################################

# Length of wire 1 (parabola)

L1 = 0.0

y = 2.0

while y >= -2.0:

    dx = 2.0*y*dy

    dL1 = math.hypot(dx,dy)

    L1 = L1 + dL1

    y = y + dy

#######################################

# Length of wire 2 (straight)

L2 = 4.0

#######################################

# Wire resistances and currents

R1 = L1*p1
R2 = L2*p2

I1 = V/R1
I2 = V/R2

#######################################

# Calculate field at A
# Biot Savart
# Assume u0 = 4*pi

y = 2.0

BA = 0.0

while y >= -2.0:

    y1 = y
    y2 = y

    x1 = y1**2.0
    x2 = 4.0

    dy1 = dy
    dy2 = dy

    dx1 = 2.0*y1*dy1
    dx2 = 0.0

    rx1 = xA - x1
    ry1 = yA - y1

    rx2 = xA - x2
    ry2 = yA - y2

    r1 = math.hypot(rx1,ry1)
    r2 = math.hypot(rx2,ry2)

    dB1 = I1*(dx1*ry1 - dy1*rx1)/(r1**3.0)
    dB2 = I2*(dx2*ry2 - dy2*rx2)/(r2**3.0)

    BA = BA + dB1 + dB2

    y = y + dy

#######################################

# Calculate field at B
# Biot Savart
# Assume u0 = 4*pi

y = 2.0

BB = 0.0

while y >= -2.0:

    y1 = y
    y2 = y

    x1 = y1**2.0
    x2 = 4.0

    dy1 = dy
    dy2 = dy

    dx1 = 2.0*y1*dy1
    dx2 = 0.0

    rx1 = xB - x1
    ry1 = yB - y1

    rx2 = xB - x2
    ry2 = yB - y2

    r1 = math.hypot(rx1,ry1)
    r2 = math.hypot(rx2,ry2)

    dB1 = I1*(dx1*ry1 - dy1*rx1)/(r1**3.0)
    dB2 = I2*(dx2*ry2 - dy2*rx2)/(r2**3.0)

    BB = BB + dB1 + dB2

    y = y + dy

#######################################

# Print results

print dy
print ""
print BA
print BB
print ""
print (BB/BA)


#>>> 
#-1e-05

#-0.175718946053
#4.86307469572

#-27.6753008424
#>>> ================================ RESTART ================================
#>>> 
#-1e-06

#-0.175719730594
#4.86307517897

#-27.6751800298
#>>>

1 Helpful 1 Interesting 1 Brilliant 0 Confused
Karan Chatrath
May 29, 2020

Code-based solution only provided. I chose this route as I did not want to manipulate expressions. 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
 
clear all
clc

% Applied voltage:
V = 10;

% Numerical resoloution:
dy = 1e-5;

% Resistances per unit length:
rho1 = 2;
rho2 = 1;

% Computation of resistances of the parabolic and straight wires:
R1 = 0;
R2 = 0;

for y = -2:dy:2

    dR1 = rho1*sqrt(1+4*y^2)*dy;
    R1  = R1 + dR1;

    dR2 = rho2*dy;
    R2  = R2 + dR2;
end

% Current flowing through parabolic and straight wires respectively:
I1 = V/R1;
I2 = V/R2;

% Net magnetic field computed at (2,0,0) due to both wires:
rp1 = [2;0;0];
Ba  = [0;0;0];

for y = -2:dy:2

    % Position and arc length element vectors:
    r1  = [y^2;y;0];
    dr1 = [2*y;1;0]*dy;

    r2  = [4;y;0];
    dr2 = [0;1;0]*dy;

    R1   = rp1 - r1;
    R2   = rp1 - r2;

    % Biot-Savart:
    dB1 = (I1*cross(dr1,R1))/(norm(R1)^3);
    dB2 = (I2*cross(dr2,R2))/(norm(R2)^3);

    % Numerical Integration:
    Ba  = Ba + (dB1+dB2);
end

% Net magnetic field computed at (5,0,0) due to both wires:
rp2 = [5;0;0];
Bb  = [0;0;0];


for y = -2:dy:2

    % Position and arc length element vectors:
    r1  = [y^2;y;0];
    dr1 = [2*y;1;0]*dy;

    r2  = [4;y;0];
    dr2 = [0;1;0]*dy;

    R1   = rp2 - r1;
    R2   = rp2 - r2;

    % Biot-Savart:
    dB1 = (I1*cross(dr1,R1))/(norm(R1)^3);
    dB2 = (I2*cross(dr2,R2))/(norm(R2)^3);

    % Numerical Integration:
    Bb  = Bb + (dB1+dB2);
end

% Answers:

% Bb = 0.1757
% Ba = -4.8631
% Bb/Ba = -27.67

1 Helpful 1 Interesting 1 Brilliant 0 Confused

@Karan Chatrath please help me in this problem, I will share my opinion if you say yes.

Thanks in advance

A Former Brilliant Member - 1 year ago

Log in to reply

Sure, I'll try. What is your attempt?

Karan Chatrath - 1 year ago

Log in to reply

@Karan Chatrath sir i am not able to start this problem due to this reasons
1) conservation of momentum se aage kuch dikh nhi rha hai.
2) Jab vo instant aayega, minimum approach wala, to dono ka x direction me velocity zero hoga par y direction ka mujhe nii pata.
3) kya tab y direction me bhi velocity 0 hona chahiye??????
4) Jab maine enregy conserve karne ki sochi to initial energy system ki hogi E i n i t i a l = K q 2 2 l E_{initial}=\frac{Kq^{2}}{2l}
5) Uske baad finally jab vo moment aayega tab velocity kya hogi , agar y direction me hui to kuch galat ho jaayega.
I have shared my all views .
Hope you understand my feelings.

A Former Brilliant Member - 1 year ago

Log in to reply

@A Former Brilliant Member – Okay so I took: ϵ o = m = q = 1 \epsilon_o=m=q=1 , L = 2 L=2 , v = 0.1 v=0.1 and I solved the equations of motion and the minimum separation I get is 2.6619. I don't think I am correct, but could you substitute these values and check whether my calculation agrees with the answer in the book? Thanks in advance.

Karan Chatrath - 1 year ago

Log in to reply

@Karan Chatrath – @Karan Chatrath No ,sir your are correct . Please share your explanatory solution.
Thanks in advance.

A Former Brilliant Member - 1 year ago

Log in to reply

@A Former Brilliant Member – It will take me quite a bit of time to type, but I suggest that you try deriving the equations of motion. No need to solve. If you can't do that, then I will type it out later. Maybe even post a problem similar to this.

  1. At any point of time t t , the midpoint of the string is moving along Y with a constant velocity v v . The motion of each mass will be symmetrical about the Y axis. Let the coordinate of the mass on the right be ( x , y ) (x,y) . Use the fact that the length of the string remains constant to derive a constraint equation. DOuble differentiate that and you will get your first equation.

  2. The forces that cause the masses to move are electrostatic and tension on the string. Apply Newton's law along the X and Y direction to get your second and third equations.

Use these three equations to solve for acceleration along x x acceleration along y y and tension. The final equations will be very complex differential equations. I solved it numerically beyond that point.

If I can think of a better way of solving it, I will let you know.

Karan Chatrath - 1 year ago

Log in to reply

@Karan Chatrath – @Karan Chatrath what is order of that differential equation?

A Former Brilliant Member - 1 year ago

Log in to reply

@A Former Brilliant Member – @Karan Chatrath This is the book solution, which is very small and it seems me incorrect also. In your opinion it is correct or not??

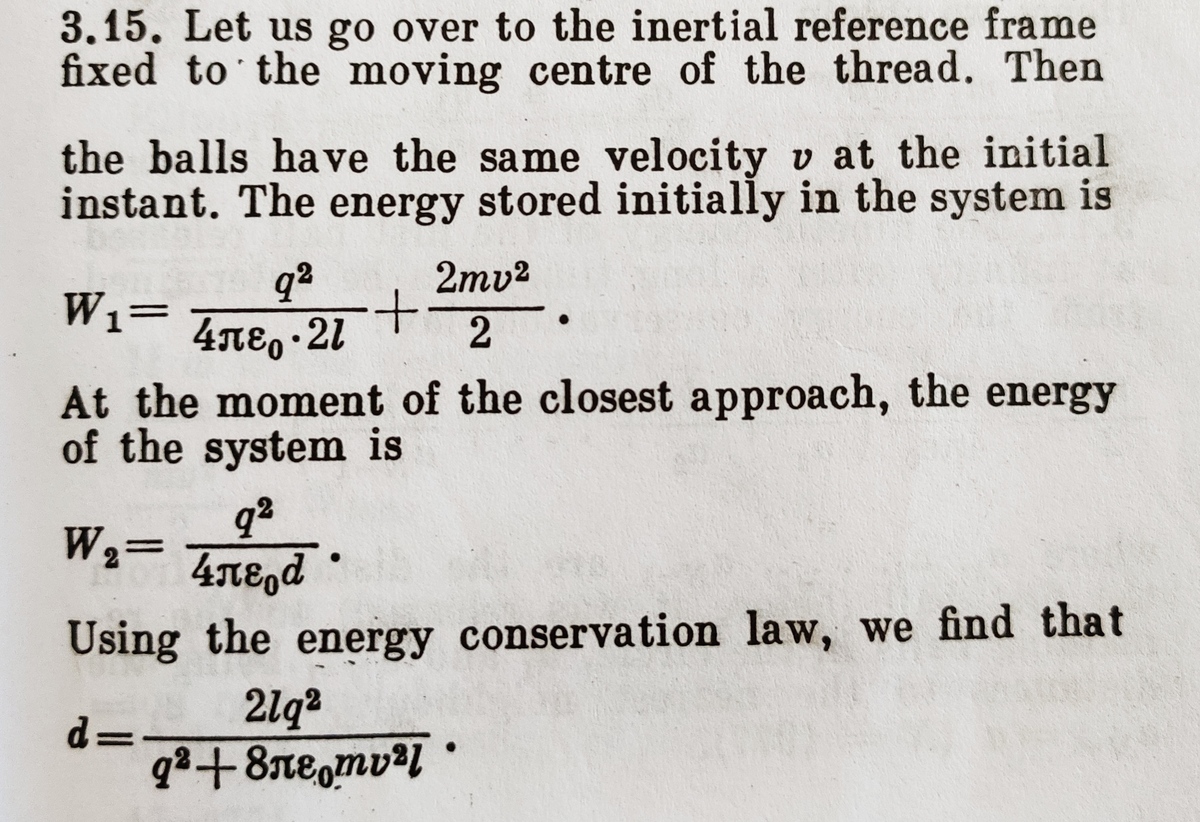
A Former Brilliant Member - 1 year ago

Log in to reply

@A Former Brilliant Member – No, this does not make sense to me.

Karan Chatrath - 1 year ago

@A Former Brilliant Member – Second-order and nonlinear and coupled, so I do not know how to solve that analytically. The acceleration along x x looks like this:

x ¨ = − 400 x ˙ 2 x 3 + 400 y ˙ 2 x 3 − 80 y ˙ x 3 − K t 2 + 20 K t y + 4 x 3 − 100 K y 2 4 x 2 ( t 2 − 20 t y + 100 x 2 + 100 y 2 ) \ddot{x}=-\frac{400\,{\dot{x}}^2\,x^3+400\,{\dot{y}}^2\,x^3-80\,\dot{y}\,x^3-K\,t^2+20\,K\,t\,y+4\,x^3-100\,K\,y^2}{4\,x^2\,\left(t^2-20\,t\,y+100\,x^2+100\,y^2\right)}

Karan Chatrath - 1 year ago

Log in to reply

@Karan Chatrath – @Karan Chatrath Sir in discussion of electricity and magnetism , @Steven Chase sir has recently uploaded the solution of this problem, and according to his opinion, the solution of the book is correct. Can you please discuss with him, if you both share each other views in that discussion note I will be happy.

A Former Brilliant Member - 1 year ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...