Magnetism Series #3
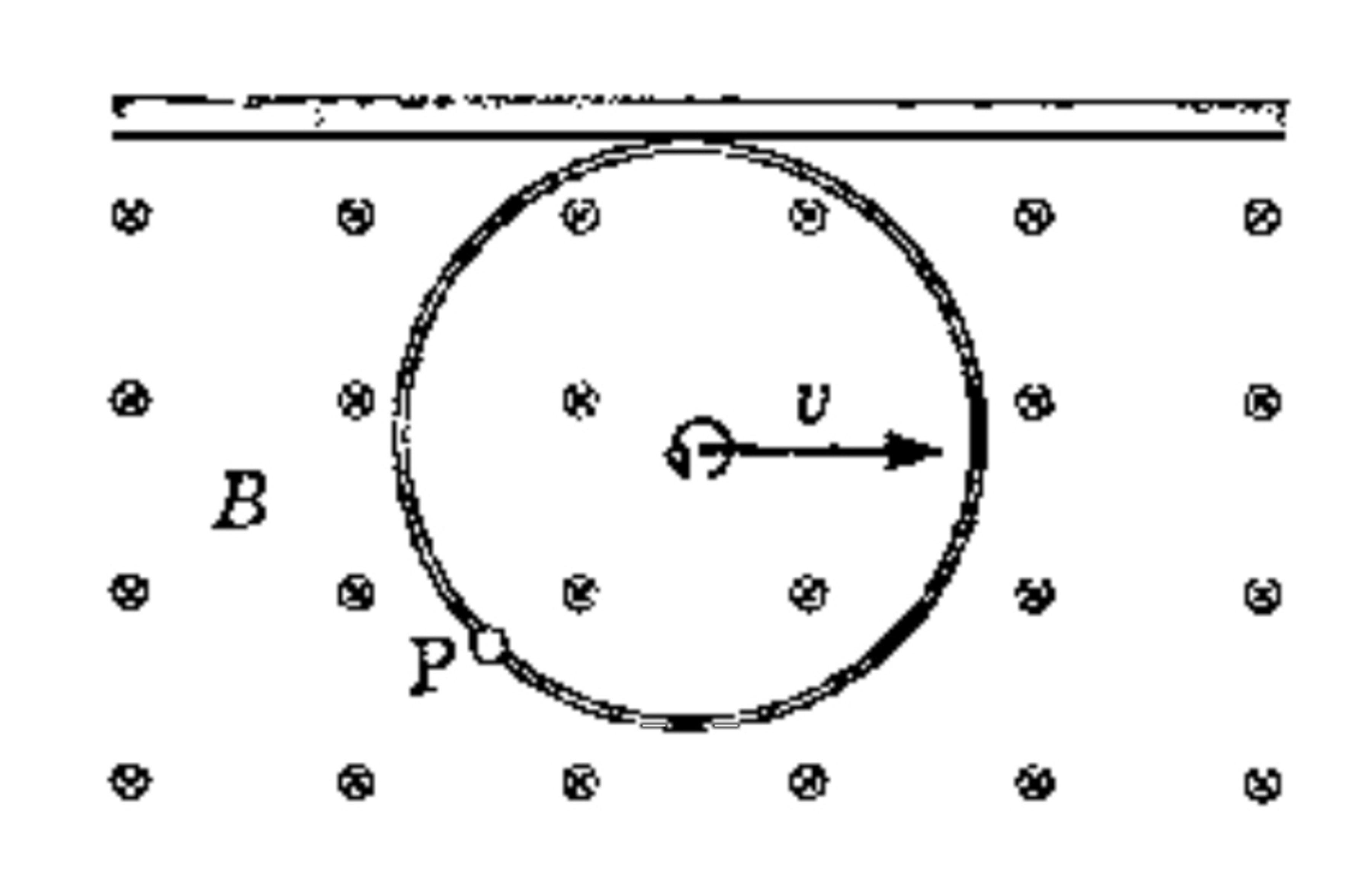
A rigid ring is made to roll along the ceiling of a room, where a horizontal uniform and static magnetic field of induction
exits perpendicular exists perpendicular to the plane of the ring. Velocity of the centre of the ring is constant and its modulus is
.A charge particle
of mass
is fixed on the ring. What should the charge
on the particle and radius
of the ring be so that there is no force of interaction between the ring and the particle?
Type your answer as
The problem is taken from my Physics Book.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider an inertial frame of reference where the X-axis points horizontally to the right and the Y-axis points upwards. Let the angular velocity of the ring be ω . The coordinates of the point are, at a general instant of time:
x = v t + R sin ω t y = − R − R cos ω t
The position vector of this point is:
r = x i ^ + y j ^ ⟹ r = ( v t + R sin ω t ) i ^ + ( − R − R cos ω t ) j ^
The velocity vector is, therefore:
v = d t d r = ( v + R ω cos ω t ) i ^ + ( R ω sin ω t ) j ^
Since the ring is purely rolling:
v = R ω
⟹ v = ( v + v cos ω t ) i ^ + ( v sin ω t ) j ^
The magnetic force on the particle is:
F B = q ( v × B ) = q v B ( − sin ω t i ^ + ( 1 + cos ω t ) j ^ )
The gravitational force on the particle is:
F G = − m g j ^
The total force on the particle is:
F = F B + F G = − q v B sin ω t i ^ + ( q v B ( 1 + cos ω t ) − m g ) j ^
The acceleration of the particle is:
a = d t d v = − R ω 2 sin ω t i ^ + R ω 2 cos ω t j ^
Newton's second law:
F = m a
Equating the X and Y components of LHS and RHS, one gets the following equations:
q v B = m R ω 2 = m g v = R ω
Solving these gives:
R = g v 2 q = B v m g