Magnetism Series #4
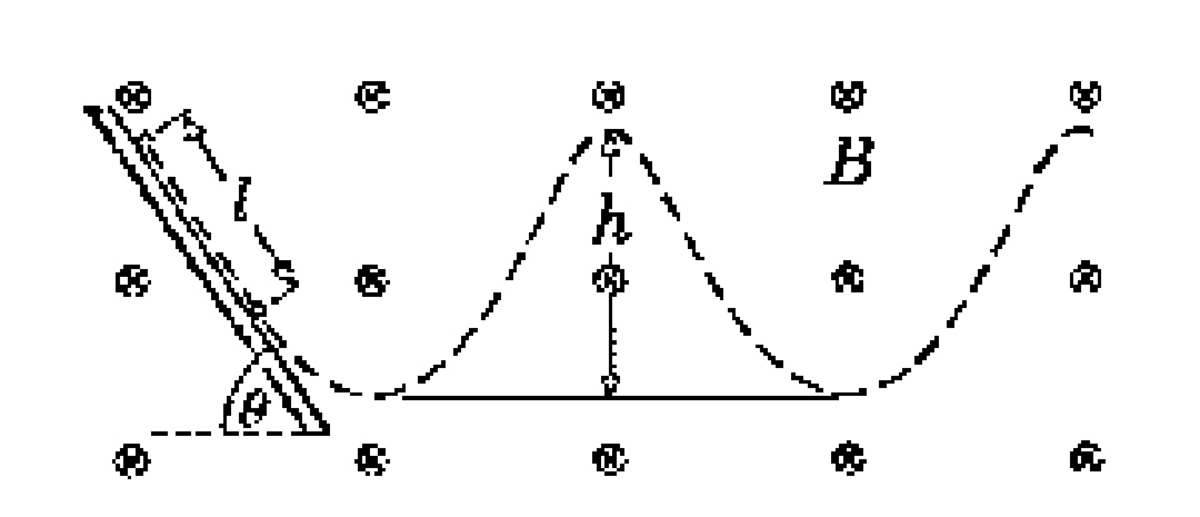
A charge particle starts sliding down a frictionless slope of inclination
θ
in presence of a horizontal uniform and static magnetic field of induction
B
directed perpendicularly into the plane of the figure and uniform gravitational field of the earth. Intensity of the gravitational field is
g
.
After sliding an unknown distance
l
the particle leaves the slope and follows a cycloidal trajectory as shown in the figure. If on the trajectory maximum vertical displacement of the particle is
h
,
Find the distance
l
it had slid on the slope.
The answer comes in the form of
l
=
β
h
cot
α
θ
Type your answer as α + β = ?
The problem is taken from my Physics Book.
Thanks in advance if you are going to post solution.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath
why it is
cos
2
θ
at the 7th step ?
It should be
cos
θ
.
@Karan Chatrath Thanks for the. Solution.
@Karan Chatrath
why is the distance
basically twice it's amplitude?
What are the two succesive crests?
Log in to reply
I realised that 'crest' is the wrong word here too. I have edited my solution again. If you look at the solution for y :
y = A o 2 + B o 2 sin ( ω t + ϕ ) + ω 2 K
You see that when the sin term is − 1 then y is:
y m i n = − A o 2 + B o 2 + ω 2 K
when the sine term is + 1 , then:
y m a x = A o 2 + B o 2 + ω 2 K
Therefore:
h = y m a x − y m i n
⟹ h = 2 A o 2 + B o 2
@Karan Chatrath
I think it is Trough ,
According to wave mechanics.
@Karan Chatrath I think the mistake in my solution is the moment the particle leaves the wedge, a new journey of particle begins which can't be related with the journey of sliding. Am I right?
Log in to reply
Yes, that is indeed what you have done. The motion along the incline cannot be related to the motion in free space.
Commented code solution below, along with a plot of the motion:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
|
@Steven Chase
Thanks,,
Can we make anayltical solution using the code?
Log in to reply
To get an analytic solution, you would have to reduce the problem to a well-defined set of differential equations. And then use a symbolic solver (like Wolfram alpha). Numerical techniques can help you find the numerical parameters α and b e t a if you are given the form of the answer. But such techniques cannot give you the form of the answer.
@Steven Chase can I show you my anayltical attempt?
Log in to reply
Sure. I'm going to upload a solution to problem 37 soon
Log in to reply
@Steven Chase will it be Anayltical?
Here is my attempt. Consider a coordinate system placed at the point at which the particle just starts moving along the incline. The X-axis faces rightward and the Y-axis faces upwards.
Firstly, we consider the motion of the particle along the incline. As the particle slides down the incline, the magnetic force acting on it is perpendicular to the incline, so the acceleration of the particle along the downward slope of the incline is:
a = g sin θ ⟹ v = g sin θ t
Balancing forces along the perpendicular direction of the incline gives:
m g cos θ = N + q v B
At the instant when the particle loses contact, the above equation becomes:
m g cos θ = q v B ⟹ v = q B m g cos θ
The velocity along the X direction at this instant is:
v o x = v cos θ = q B m g cos 2 θ v o y = − v sin θ = − q B m g sin θ cos θ
Now, looking at the instant when the particle loses contact, we have:
m g cos θ = q v B ⟹ m g cos θ = q B g sin θ t o ⟹ t o = q B m cot θ
⟹ v = g sin θ t
Displacement along the incline:
s = 2 g sin θ t 2
At the instant of loss of contact:
L = 2 g sin θ t o 2 L = 2 q 2 B 2 sin θ m 2 g cos 2 θ
The X and Y coordinates of the particle at this instant are:
x o = L cos θ y o = L sin θ
Now that the particle has lost contact with the incline, this instant from now is considered to have occurred at time t = 0 . When the particle loses contact with the incline, Newton's second law can be applied to find the equations of motion:
m a = q ( v × B ) − m g j ^
Simplifying these equations gives the following differential equations:
m x ¨ = − q B y ˙ m y ¨ = q B x ˙ − m g x ( 0 ) = x o ; y ( 0 ) = y o x ˙ ( 0 ) = v o x ; y ˙ ( 0 ) = v o y
Consider the equation:
m x ¨ = − q B y ˙
Integrating both sides:
m x ˙ = − q B y + C
Where C is an integration constant. Applying initial conditions and solving for C gives:
v x = − m q B y + 2 q B m g cos 2 θ
Plugging this result into the differential equation for y ¨ gives:
y ¨ = − m 2 q 2 B 2 y + g ( 2 cos 2 θ − 1 )
Let:
ω = m q B K = g ( 2 cos 2 θ − 1 ) The general solution is:
y = A o sin ω t + B o cos ω t + ω 2 K
The unknown constants A o and B o can be found by applying the initial conditions and solving gives the following:
A o = − q 2 B 2 m 2 g sin θ cos θ B o = q 2 B 2 m 2 g sin 2 θ
Now:
y = A o sin ω t + B o cos ω t + ω 2 K y = A o 2 + B o 2 sin ( ω t + ϕ ) + ω 2 K
The amplitude:
A o 2 + B o 2 = 2 L tan 2 θ
Looking at the diagram, one can see that h is the vertical distance between the maximum and minimum of the cycloid. This distance is basically twice this amplitude. This implies that:
h = 2 A o 2 + B o 2 = 4 L tan 2 θ ⟹ L = 4 h cot 2 θ