Magnetism Series #1

Electricity and Magnetism Level 2

Two particles of equal mass $m$ and having unlike charges of modulus $q$ each are placed in free space a distance $r$ apart. A uniform and constant magnetic field of induction $B$ is established everywhere perpendicular to the line joining the particles and the particles are released. If the magnetic field is sufficient to avoid collision of the particles, find the minimum separation between the particles.

Details and Assumptions
1) $m=100$
2) $r=2$
3) $B=3$
4) $\epsilon_{0}=4$

The problem is taken from my Physics Book.

The answer is 1.746.

2 solutions

Karan Chatrath
Aug 29, 2020

Guidelines for an analytical solution.

The motion of each charge is symmetric about the Y axis. Therefore the electric force on the charge in the first quadrant is always along the negative X direction. Applying Newton's second law in 2-D gives:

$m \vec{a} = -\frac{Kq^2}{4x^2} \ \hat{i} + q (\vec{v} \times \vec{B})$

Derivation of the above is straightforward. Simplifying the above equation gives two coupled differential equations as such:

$\ddot{x} = -\frac{Kq^2}{4mx^2} + \frac{Bq\dot{y}}{m}$ $\ddot{y} =-\frac{Bq\dot{x}}{m}$

Integrating the second equation:

$\dot{y} =-\frac{Bqx}{m} +C$

Where $C$ is the integration constant. Applying initial conditions $x(0)=1$ gives:

$\dot{y} =\frac{Bq}{m}(1-x)$

Substituting the above result in the equation for acceleration along $x$ gives:

$\ddot{x} = -\frac{Kq^2}{4mx^2} + \frac{B^2q^2(1-x)}{m^2}$

$\implies \ddot{x} = f(x)$

The RHS is purely an expression in terms of $x$ . Now:

$\ddot{x} = \dot{x} \frac{d \dot{x}}{dx} = f(x)$ $\implies \dot{x} d(\dot{x}) = f(x) \ dx$

Integrating both sides and applying initial conditions:

$\int_{0}^{\dot{x}}\dot{x} d(\dot{x}) =\int_{1}^{x} f(x) \ dx$ $\implies \frac{\dot{x}^2}{2} = \int_{1}^{x} f(x) \ dx$

The minimum separation between particles occurs when $\dot{x} = 0$ . The integral on the RHS evaluates to a non-linear expression where the numerator is a cubic equation. Solving for $\dot{x}=0$ essentially means solving for the roots of that resulting cubic equation. Note that $x=1$ is a solution of that equation as the particle is initially at rest. Using this, the cubic equation can be converted into a quadratic equation. The solution needs to be multiplied by 2 to obtain the minimum separation.

@Karan Chatrath the charge in the first quadrant is positive and the charge in the second quadrant is negative.
Both will attrach each other.
So the charge of 1st quadrant will experience a force toward right side which is +x direction.

Talulah Riley - 9 months, 2 weeks ago

I don't know how else to explain to you. A force to the right would mean that charges repel, which is not so.

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath I also don't know how should I explain you. Leave it. By the way try my new problems. And if possible try to post solution.
You are a real Legend of Physics.

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – @Karan Chatrath Oh I was thinking 2nd quadrant as 1st quadrant and 2nd quadrant as 1 quadrant.
Now everything is clear.
Thanks for bearing the pain for such a stupid mistake.

Talulah Riley - 9 months, 2 weeks ago

@Karan Chatrath sir can we generalise this result? I am facing difficulty while doing that.
I will show my attempt if you reply me yes?
Thanks ina advance.

Talulah Riley - 9 months, 2 weeks ago

I don't think it can be generalised. If the magnetic field is itself time-varying But you may shw or spatially varying, this problem becomes quite difficult. But you may show your attempt.

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath Sir generalisation means just don't put values and solve till the end.
Here below I have posted my attempt, but the end when I put the values I didn't get the answer.

Talulah Riley - 9 months, 2 weeks ago

@Karan Chatrath please check the solution, because at the end when I put the value I didn't get the answer
Please correct me if I am wrong.

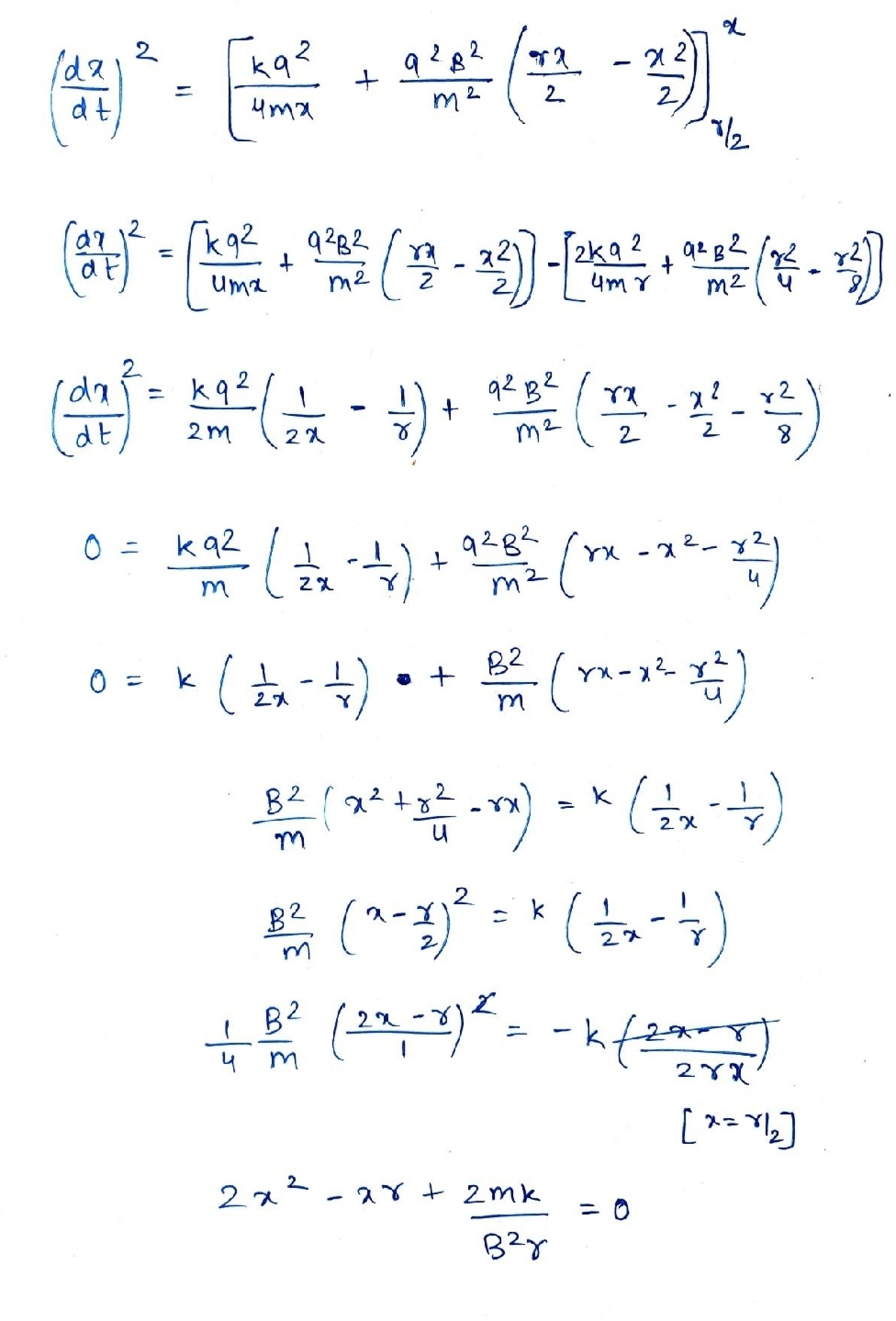
Thanks in advance.

Talulah Riley - 9 months, 2 weeks ago

When you integrate $\dot{x} \ d\dot{x}$ you make a small mistake there. See if you can spot it.

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath But still it will not make any sense, because at the end we have put $\frac{dx}{dt}=0$ .
?

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – @Karan Chatrath sir you didn't give me reply after this.
Please reply whenever you get free.

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – Yes, it is because it is not easy to spot the mistake. After a cursory glance, I think you should recheck the steps after applying the limits of integration on the RHS.

Karan Chatrath - 9 months, 2 weeks ago

Steven Chase
Aug 27, 2020

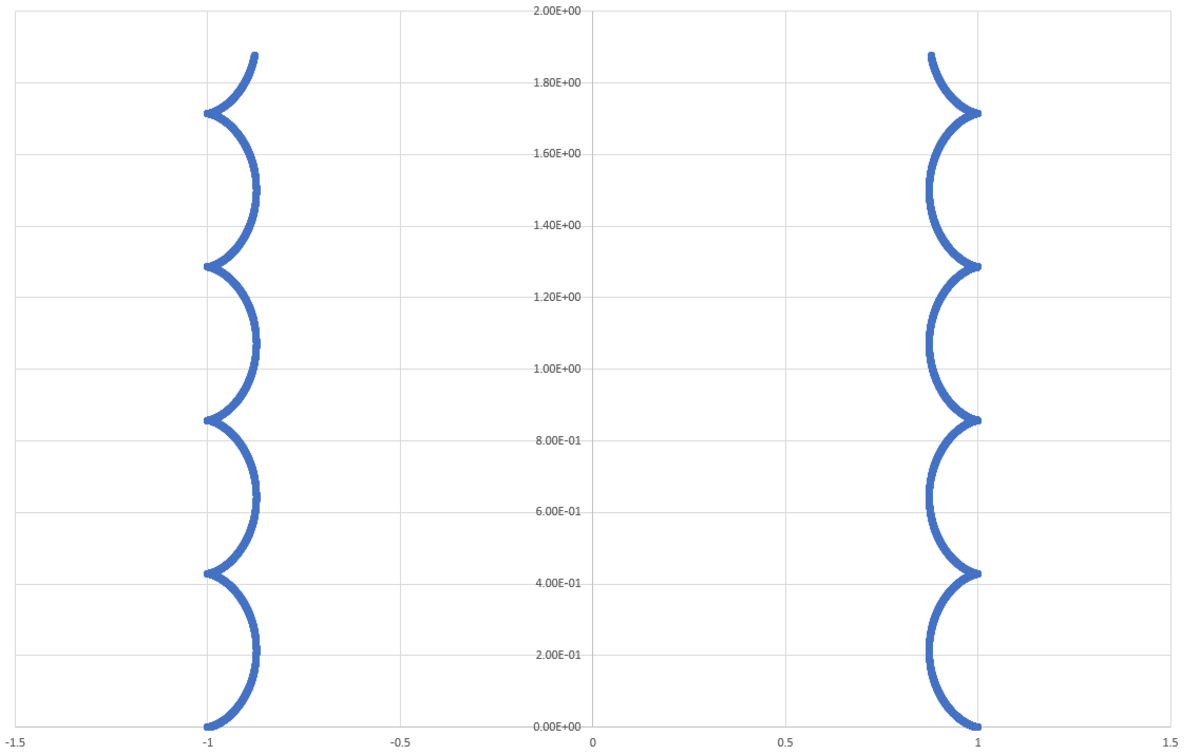
Nice one. I just ran a numerical simulation for this. The path of the two particles is plotted below for $q = 20$ until $t = 50$ . No matter which $q$ value is chosen, the minimum separation is always $\approx 1.746$ .

import math

dt = 10.0**(-5.0)

m = 100.0
r = 2.0
B = 3.0
e0 = 4.0

###########################

Bx = 0.0
By = 0.0
Bz = B

k = 1.0/(4.0*math.pi*e0)

q = 20.0

q1 = q
q2 = -q

###########################

t = 0.0
count = 0

x1 = r/2.0
y1 = 0.0
z1 = 0.0

x2 = -r/2.0
y2 = 0.0
z2 = 0.0

x1d = 0.0
y1d = 0.0
z1d = 0.0

x2d = 0.0
y2d = 0.0
z2d = 0.0

x1dd = 0.0
y1dd = 0.0
z1dd = 0.0

x2dd = 0.0
y2dd = 0.0
z2dd = 0.0

###########################

# Dsq = (x1-x2)**2.0 + (y1-y2)**2.0 + (z1-z2)**2.0

Dsqd = 2.0*(x1-x2)*(x1d-x2d) + 2.0*(y1-y2)*(y1d-y2d) + 2.0*(z1-z2)*(z1d-z2d)

Dmin = 9999999.0

#while Dsqd <= 0.0:
while t <= 50.0:

    x1 = x1 + x1d*dt
    y1 = y1 + y1d*dt
    z1 = z1 + z1d*dt

    x2 = x2 + x2d*dt
    y2 = y2 + y2d*dt
    z2 = z2 + z2d*dt

    x1d = x1d + x1dd*dt
    y1d = y1d + y1dd*dt
    z1d = z1d + z1dd*dt

    x2d = x2d + x2dd*dt
    y2d = y2d + y2dd*dt
    z2d = z2d + z2dd*dt

    Dx = x1 - x2
    Dy = y1 - y2
    Dz = z1 - z2

    D = math.sqrt(Dx**2.0 + Dy**2.0 + Dz**2.0)

    if D < Dmin:
        Dmin = D

    Dsqd = 2.0*(x1-x2)*(x1d-x2d) + 2.0*(y1-y2)*(y1d-y2d) + 2.0*(z1-z2)*(z1d-z2d)

    ux = Dx/D
    uy = Dy/D
    uz = Dz/D

    FE = k*q1*q2/(D**2.0)

    FE1x = FE*ux
    FE1y = FE*uy
    FE1z = FE*uz

    FE2x = -FE1x
    FE2y = -FE1y
    FE2z = -FE1z

    cross1x = y1d*Bz - z1d*By
    cross1y = -(x1d*Bz - z1d*Bx)
    cross1z = x1d*By - y1d*Bx

    cross2x = y2d*Bz - z2d*By
    cross2y = -(x2d*Bz - z2d*Bx)
    cross2z = x2d*By - y2d*Bx

    FB1x = q1*cross1x
    FB1y = q1*cross1y
    FB1z = q1*cross1z

    FB2x = q2*cross2x
    FB2y = q2*cross2y
    FB2z = q2*cross2z

    F1x = FE1x + FB1x
    F1y = FE1y + FB1y
    F1z = FE1z + FB1z

    F2x = FE2x + FB2x
    F2y = FE2y + FB2y
    F2z = FE2z + FB2z

    x1dd = F1x/m
    y1dd = F1y/m
    z1dd = F1z/m

    x2dd = F2x/m
    y2dd = F2y/m
    z2dd = F2z/m

    t = t + dt
    count = count + 1

    if count % 1000 == 0:
        print t,x1,y1
        print t,x2,y2

###########################

print ""
print ""

print dt
print t
print q
print Dmin

@Steven Chase Nice solution.
Hope anyone will post a anayltical solution.

Talulah Riley - 9 months, 2 weeks ago

@Steven Chase
Would you like to solve the problem analytically?
The code seems me very big.

Talulah Riley - 9 months, 2 weeks ago

This problem is actually a more difficult version of that charge separation problem you posted earlier. I don't think I will try to solve analytically, given that the numerical solution is so easy

Steven Chase - 9 months, 2 weeks ago

@Steven Chase The problem has a answer given in my book.i have set the numerical value for you.
It means that anayltical solution should exist.

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – @Steven Chase The problem with the book is that, solutions are not available.

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – Have you tried Googling the problem text, or portions of it?

Steven Chase - 9 months, 2 weeks ago

@Steven Chase – @Steven Chase Yeah, but nothing comes.

Talulah Riley - 9 months, 2 weeks ago

@Steven Chase So what are you thinking sir?
I have done whatsapp this physics question to my physics teacher but he is not bothered to reply me.

Talulah Riley - 9 months, 2 weeks ago

I think I've done everything I'm going to do. Maybe somebody else will post an analytical solution later

Steven Chase - 9 months, 2 weeks ago

@Steven Chase I have posted a new problem.

Talulah Riley - 9 months, 2 weeks ago

Guidelines for an analytical solution. For some reason, I cannot post a solution in the regular way. Would like to know your thoughts on it. I have left out the number crunching and evaluations.

$m \vec{a} = -\frac{Kq^2}{4x^2} \ \hat{i} + q (\vec{v} \times \vec{B})$

Derivation of the above is straightforward. Simplifying the above equation gives two coupled differential equations as such:

$\ddot{x} = -\frac{Kq^2}{4mx^2} + \frac{Bq\dot{y}}{m}$ $\ddot{y} =-\frac{Bq\dot{x}}{m}$

Integrating the second equation:

$\dot{y} =-\frac{Bqx}{m} +C$

Where $C$ is the integration constant. Applying initial conditions $x(0)=1$ gives:

$\dot{y} =\frac{Bq}{m}(1-x)$

Substituting the above result in the equation for acceleration along $x$ gives:

$\ddot{x} = -\frac{Kq^2}{4mx^2} + \frac{B^2q^2(1-x)}{m^2}$

$\implies \ddot{x} = f(x)$

The RHS is purely an expression in terms of $x$ . Now:

$\ddot{x} = \dot{x} \frac{d \dot{x}}{dx} = f(x)$ $\implies \dot{x} d(\dot{x}) = f(x) \ dx$

Integrating both sides and applying initial conditions:

$\int_{0}^{\dot{x}}\dot{x} d(\dot{x}) =\int_{1}^{x} f(x) \ dx$ $\implies \frac{\dot{x}^2}{2} = \int_{1}^{x} f(x) \ dx$

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath you should post a solution, because the hardwork you have done is really appreciable, instead of this post it as a solution.
By the way how did you $x(0) =1$
Thanks in adavnce.

Talulah Riley - 9 months, 2 weeks ago

Thanks! But I am not able to post a solution despite solving the problem correctly. I don't know why. Maybe it is a bug in the website. Anyway, $x(0)=1$ is the initial condition. The particles are separated initially by two units. See the plot shared by @Steven Chase

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath – @Karan Chatrath Ohh, The problem in my book is not in numerical so I was expecting the distance should be $\frac{r}{2}$ .
I forgot that i have posted the problem by setting numerical value.
By the way, the electric force should be in positive direction because both the charge will attract, why you have written negative sign??

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – If both charges will attract, then the charge in the 1st quadrant, which is positive will experience a force along the negative X direction.

Karan Chatrath - 9 months, 2 weeks ago

@Karan Chatrath – @Karan Chatrath Aree kaisa bhaiya jo 1 quadrant pe hai uspe +x direction pe force lagega, aur jo 2nd Quadrant oe hai uspe -x pe lagega na?

Talulah Riley - 9 months, 2 weeks ago

@Talulah Riley – Finally managed to post an explanation. And no, the charge on the 1st quad is positive and in the secind quad is negative. Think about it..

Karan Chatrath - 9 months, 2 weeks ago

@Steven Chase Sir above I have posted my anayltical solution without putting values.
At the end when I put the numerical values I didn't get the answer.
Can you take a look?

Talulah Riley - 9 months, 2 weeks ago

Magnetism Series #1

The answer is 1.746.

2 solutions

0 pending reports