Mamma Mia! Here We Go Again

First, we have that:

${ A }^{ B }={ B }^{ A }\\ \hookrightarrow \log _{ A }{ { B }^{ A } } =B\\ \quad \quad A\cdot \log _{ A }{ { B } } =B\\ \quad \quad \log _{ A }{ { B } } =\frac { B }{ A }$

Now, if $B={ A }^{ n }$ ,where n is a natural number $n>0$

$\quad \quad \log _{ A }{ { { A }^{ n } } } =\frac { { A }^{ n } }{ A } \\ n={ A }^{ n-1 }$

So, if $n=1$ , we have that $A=B$ which gives 100 solutions.

If $n=2$ , we have $(2,4) and (4,2)$ .

If $n>2$ we don't have any solutions.

Thus, we have 102 solutions.

We can try to give an analytical proof here. The motivation comes from $A^B = B^A \Longleftrightarrow A^{\frac{1}{A}} = B^{\frac{1}{B}}$ .

For $A = B$ , both sides are equal, in which case there are 100 solutions. For $A\neq B$ , we claim that only $(2,4) \text{ and } (4,2)$ are the solutions (no other $(A,B)$ can satisfy $A^{\frac{1}{A}} = B^{\frac{1}{B}}$ ). The following justifies this claim.

$\textit{Proof}:$

Let $f(x) = x^{\frac{1}{x}}$ for $x > 0$ .

By inspection, $f(1) < f(2) = f(4) < f(3)$ . Now differentiating $f$ w.r.t. $x$ yields

$\displaystyle f'(x) = \frac{x^{\frac{1}{x}}\left(1- \ln x\right)}{x^2},$

which shows that $f'(x) > 0$ when $x < e$ , $f'(x) = 0$ when $x= e$ , and $f'(x) < 0$ when $x > e$ .

Hence $f$ is strictly increasing on $(0,e]$ and strictly decreasing on $[e, \infty)$ . Then for positive integers $m,n$ with $m > n > 4 > e$ , we have $f(m) < f(n) < f(4) = f(2)$ . Now it remains to show that $f(m) > f(1) = 1$ .

Suppose the contrary that $f(m) = a \leq 1$ for some positive integer $m>4$ . Then we find that $m^{\frac{1}{m}} = a \Longrightarrow m = a^m \leq a \leq 1$ , a contradiction with the fact that $m > 4$ .

Hence for positive integers $m,n$ with $m > n > 4$ , we have

$f(1)< f(m) < f(n) < f(4) = f(2) < f(3)$ .

This, in turn, means that for every positive integer $n > 4$ , there is no $m\in \mathbb Z^+$ , with $m \neq n$ , such that $f(m) = f(n)$ , and hence this proves the claim. $\Box{\ }$

A^B = B^A. The equation is also equivalent to A^(B/A) = B and A | B for integral solutions. Let B = AK and so... A^K = AK. A = (AK)^(1/K), 1 = [A^([1-K]/K)][K^(1/K)] and so.... [A^(1-K)][K] = 1. Also equivalent to A^(K-1) = K. A = (K)^(1/(K-1)) which is integral when K =1 and K = 2. If K = 1, then A = B, so there are 100 ordered pairs of solutions. If K = 2, A = 2 and B = 4. (2,4) and (4,2) satisfies the equation. Hence, there are 102 ordered pairs of solutions.

My solution is really intuitive, no logs involved, just basic algebra.

We have that:

$A^{B} = B^{A}$

Let's assume that $B \geq A$ , so we must have that A divides B. This is the same as saying that:

$B = kA$ with $k$ positive integer. As a consequence, substituting the previous relation, we get:

$A^{kA} = (kA)^{A}$

then extracting the A-th root on both sides:

$A^{k}=kA$ which is of course: $A^{k}-kA=0$

For $k=1$ we get $A-A=0$ , which is the case of $A=B$ corresponding to 100 couples $(A,A)$ .

For $k=2$ we get $A^{2}-2A=0$ , whose solutions are $A=0$ which is not acceptable, and $A=2$ corresponding to the couples $(2,4)$ and $(4,2)$ for the symmetry of the problem.

For $k\geq 3$ we still get $A=0$ as the non-intersting solution and the absolute value of all remaining solutions equal to the $(k-1)$ -root of $k$ which turn out to be irrational for every $k\geq 3$ .

We got 100 couples from the case $k=1$ and 2 couples from the case $k=2$ , for a grand total of 102 ordinate couples that satisfy the condictions of the problem.

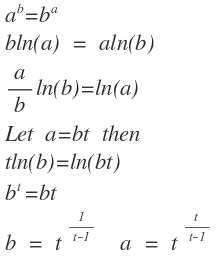
If t=2 then a=2^2 and b=2^1, therefore a=4 and b=2, if t=1, the denominator becomes 0 producing infinity. If t>2 for example if t=3. Then we have 3^(3/2) which will not be an integer. Since t^(1/(t-1) ) cannot be an integer except for t=2

(1, 1)

(2, 2)

(2, 4)

(3, 3)

(4, 2)

(4, 4)

...

(100, 100)

Obviously, 100 + 2 = 102. I checked with computing for safety even though this may not be smart.

Answer: 102

if A=B, we get 100 pairs, and other pairs obtain from (x^x)^x=x^(x^x). only 2^2 and 3^3 are < 101. so (A,B)=(2,4) and (3,27) Hence ans.102 . In between (4,2) and (27,3) are also possible ordered pairs. Correct answer will be 104