Mangle Angle Triangle
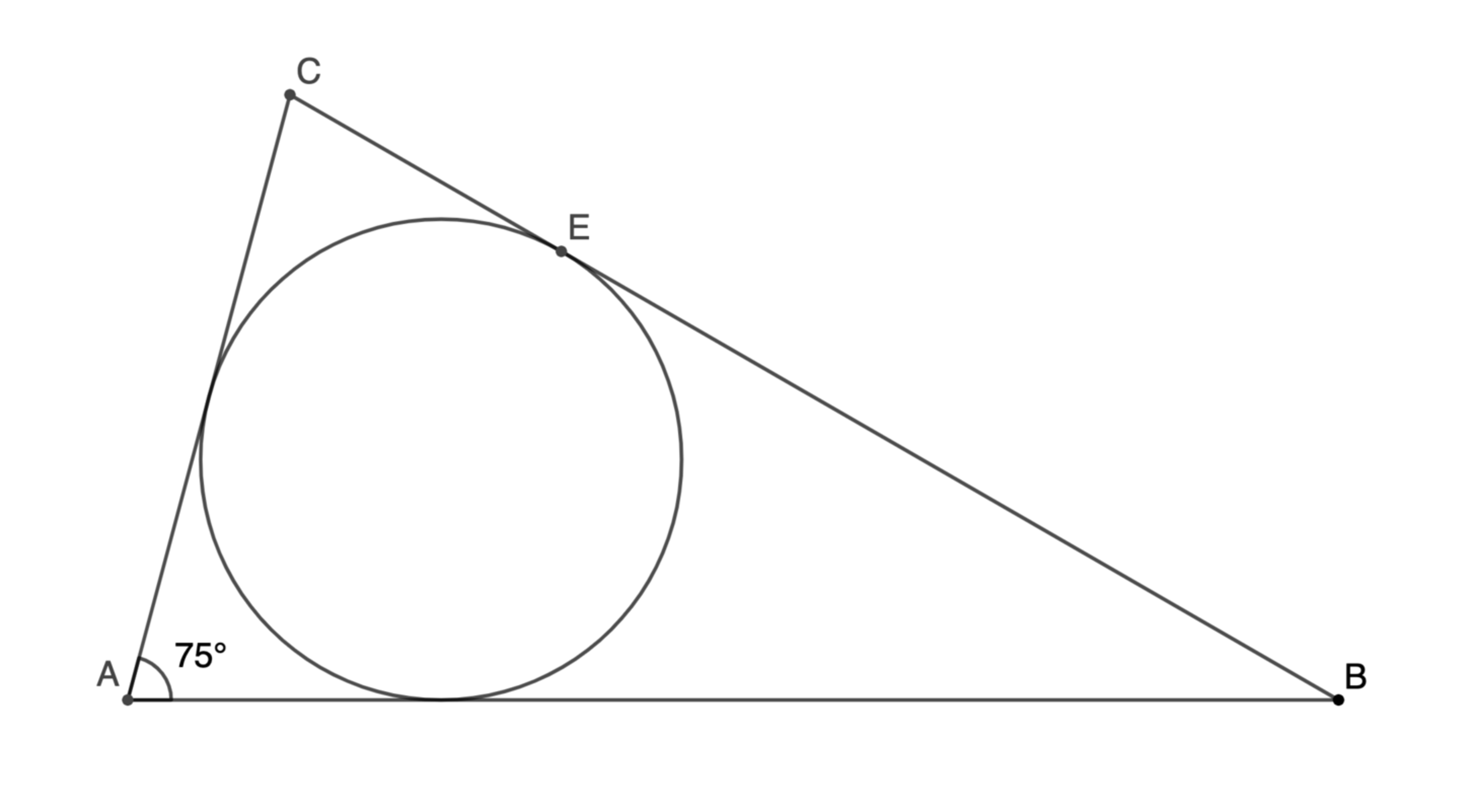
The area of △ A B C is 40. Its incircle intersects C B at E . ∠ C A B is 7 5 ∘ . What is C E ⋅ E B ?
Find a closed-form solution, convert it to decimal, and submit the sum of the first 11 digits to the right of the decimal point.
The answer is 55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
For the sake of completeness, the closed-form of C E ⋅ E B is 4 0 ( − 2 − 2 + 3 + 6 )
Can I suggest reducing the number of digits needed, I had to search for an online calculator which could do the 11.
Log in to reply
I have to agree with this. @Fletcher Mattox
A simple remedy for this is to just ask for the value to 5 significant figures. 11 seems like a huge overkill.
On the other hand, if I were the problem setter, I would have phrased it as
Let f ( x ) denote the least degree monic polynomial where the numerical value of C E ⋅ E B is one of its roots. What is f ( 1 ) ?
And the answer is 1 4 + 3 2 0 ⋅ 1 3 + 3 2 0 0 ⋅ 1 2 − 5 1 2 0 0 0 ⋅ 1 + 2 5 6 0 0 0 = 2 0 5 1 5 2 1 .
Log in to reply
Thank you! This is an excellent idea. I have been thinking along similar lines. The solution to a problem I am composing now is the root of a quartic equation. I was thinking of asking the solver to find the minimal polynomial and submit, say, the sum of its coefficients.
Log in to reply
@Fletcher Mattox – And if you think 11 digits is excessive, wait till you see the problem where I asked for 50 digits! :)
Let D be the point of tangency on A B , F be the point of tangency on A C , and O be the center of the incircle, and let a = C F = C E , b = B E = B D , and c = A F = A D .
Then the area of the triangle is given by 4 0 = 2 1 ( a + c ) ( b + c ) sin 7 5 ° , which rearranges to a b + a c + b c + c 2 = 8 0 csc 7 5 ° .
From △ O A D , the inradius is r = c tan 3 7 . 5 ° , but also r = s △ A B C A △ A B C = a + b + c 4 0 , so c tan 3 7 . 5 ° = a + b + c 4 0 , which rearranges to a c + b c + c 2 = 4 0 cot 3 7 . 5 ° .
Combining a b + a c + b c + c 2 = 8 0 csc 7 5 ° and a c + b c + c 2 = 4 0 cot 3 7 . 5 ° gives C E ⋅ E B = a b = 8 0 csc 7 5 ° − 4 0 cot 3 7 . 5 ° ≈ 3 0 . 6 9 3 0 7 9 5 1 9 1 5 8 4 , making the sum of the first 1 1 digits to the right of the decimal point 6 + 9 + 3 + 0 + 7 + 9 + 5 + 1 + 9 + 1 + 5 = 5 5 .