A Circle And A Line
What is the number of intersections between y = 4 and x 2 + y 2 = 9 ?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
When y = 4 , x 2 = − 7 which means x is a complex number, hence y = 4 does not intersect the given graph at all.
Moderator note:
That's right.
Without knowing that x 2 = − 7 , can you show that there is no real solution for x ?
Hint : Interpret x 2 + y 2 = 9 geometrically.
@Mehul Arora I cant find you on facebook. WHY?
Log in to reply
Hi @Nihar Mahajan That's right. I deactivated my account :)
Log in to reply
Again Why? :(
Log in to reply
@Nihar Mahajan – Half yearly exams, bro :3
We can always stay in touch here :)
@Nihar Mahajan – Can I add you on facebook , Please ? ^_^
Way 1 to solve : Because x^2 >= 0 so that y^2 <=9 so that -3 <= y <= 3, its graph can not meet the line y =4
Way 2 to solve : with y =4 , x^2 = -7 <0 --> the point that the graph meet the line doesn't exist.
Obviously, the value can never go beyond the square of 4.
Just solve for x , y from the two equations y = 4 ⇒ ( 1 ) , x 2 + y 2 = 9 ⇒ ( 2 ) and then the outcome of the ordered pairs ( x , y ) will be the points of intersection , and here is how :
From ( 1 ) we see that always y = 4
And by substituting y from ( 1 ) into ( 2 ) , we get x 2 + y 2 = x 2 + 4 2 = 9
∴ x 2 = 9 − 4 2 = − 7 ∴ x = ± − 7 = ± 7 i Which are apparently imaginary numbers .
But the graph requires a real values for x , y in order to get real points ( x , y ) .
Which means that there's no real ordered pairs ( x , y ) satisfying the two equations , and hence they have no meeting point on graph . i.e. 0
That eqn is a circle of radius 3 units.. And a line parallel to x axis at a distance of 4 units from origin can't pass through the circle.
Y= 4 is the y intercept parallel to x axis. Will never touch the circle of radius 3 units.
The graph of the 2nd equation is a a circle with radius 3, and the graph of the first equation is a line with y-intercept at (0,4). The line is beyond the circumference of the circle
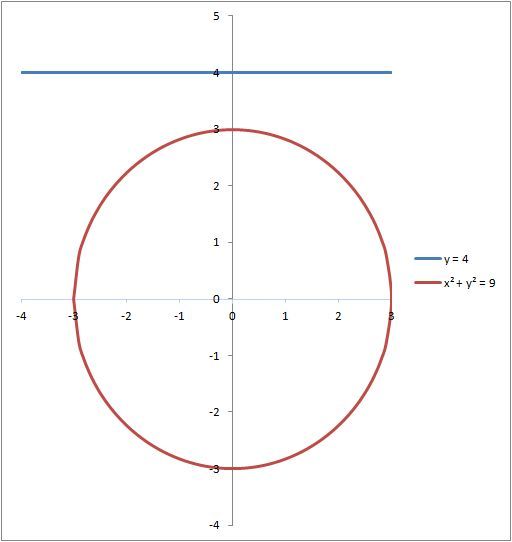
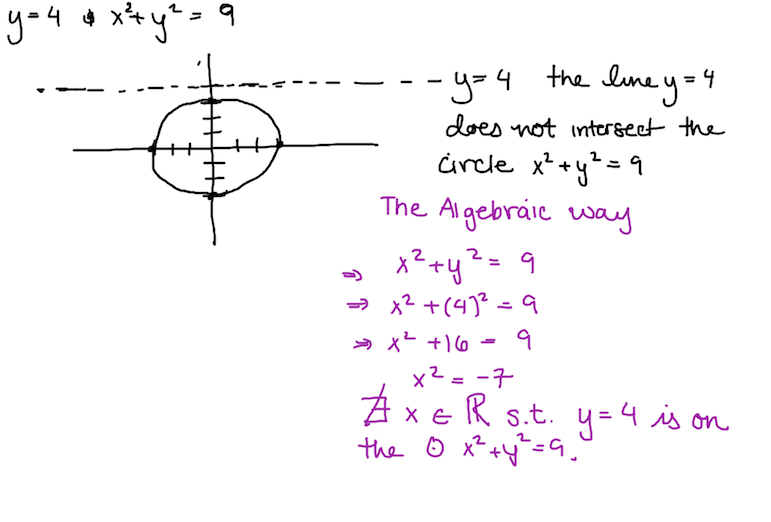
Geometrically, x 2 + y 2 = 9 is a circle of radii 3 and center on ( 0 , 0 ) so the circle doesn't go beyond y = 3 and x = 3 ∴ y = 4 doesn't meet with x 2 + y 2 = 9