Map Coloring With Some Already Done

Relevant wiki: Four Color Theorem

We can color the figure normally, apart from the top left region.

There, we run into a problem, because that region is touching 4 other colors, so we need to add a fifth color. Therefore, the minimum number is $\boxed{5}$ .

NOTE : The Four Color Map Theorem (FCMT) states that any blank map has a minimum of four colors. The FCMT doesn't always apply to maps like these. If we were to completely re-color the map to apply to the FCMT, it would look like this:

First note that every remaining region touches at least one of the red regions, so red cannot be used any more.

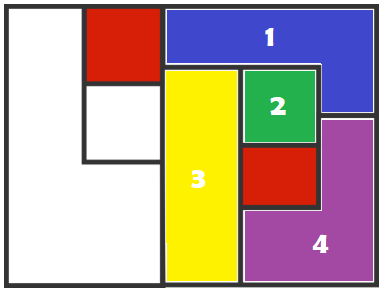
Then, notice that each of the numbered regions in the diagram above, touches all of the other 3 numbered regions. This means that 4 unique colours must be used for these regions, as shown. The remaining 2 regions can be coloured any of blue, green or purple (in either order).

Therefore, the total number required is $\boxed{5}$ . This isn't a relevant case of the four colour map theorem as some of the map is already completed.

I look for a region with the most bordering regions. There are four regions bordering another one, so 5 colors are necessary.

The middle rectangle shares an edge with all of the uncoloured sections so must have it’s own colour. Then, the sections on the right all share edges, so we must have 3 more colours. The final two sections on the left can be coloured with any 2 of the colours in the right section, so we must have 5 colours in total.

To solve this, we need to look for neighboring areas (ie areas where a simple bend is connected to other bends) and we need to count the bends that are all connected. If you look at the right half, we have 5 polygons, one of which is red. Apart from the upper polygon, the rest of the polygons are connected to the rest of the polygons, so the color chosen for each polygon should not be used in any of the other polygons, so we need 4 colors. The color that we select for a few upper limits should not be the same with several adjacent gates, and on the other hand, it can not be used in red, because the left is connected to the red polygon so a new color is needed, so a total of 5 colors are needed. The left side can also be filled with right colors because there is no connection to the right side So you need 5 colors in total