Mass Hanging from Two Springs
Initially at rest, a 30 Kg mass supported by springs is released and falls downward until it reaches equilibrium. The spring constant is k=100 N/m and the springs are configured as shown in the diagram. The supports are 6 meters apart and the mass is initially at a vertical distance of 3.5 meters from the supports. Take g=9.81 m/s^2. What is the final distance from the right support in meters? Provide your answer to the nearest 1/10th. Note: The springs are un-stretched and the distance from the right support is the resultant distance from the x and y components.
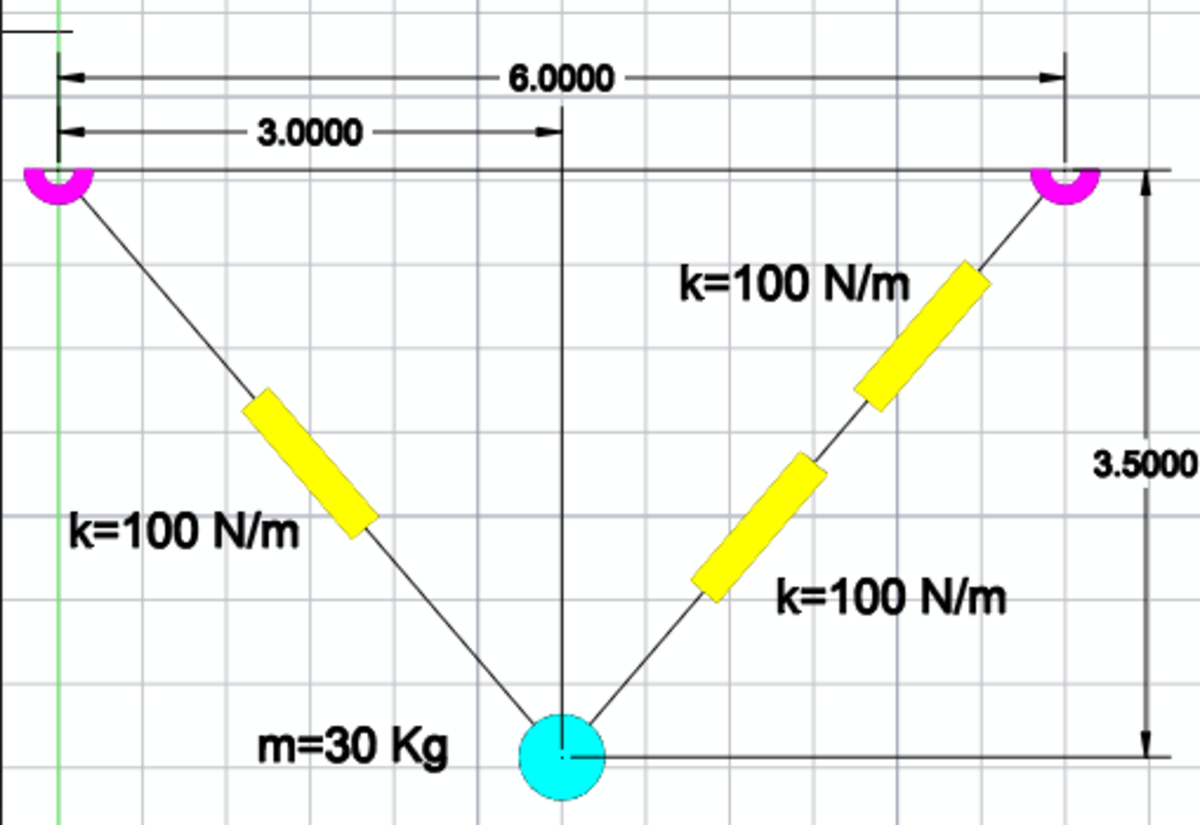
The answer is 7.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice work, Karan!
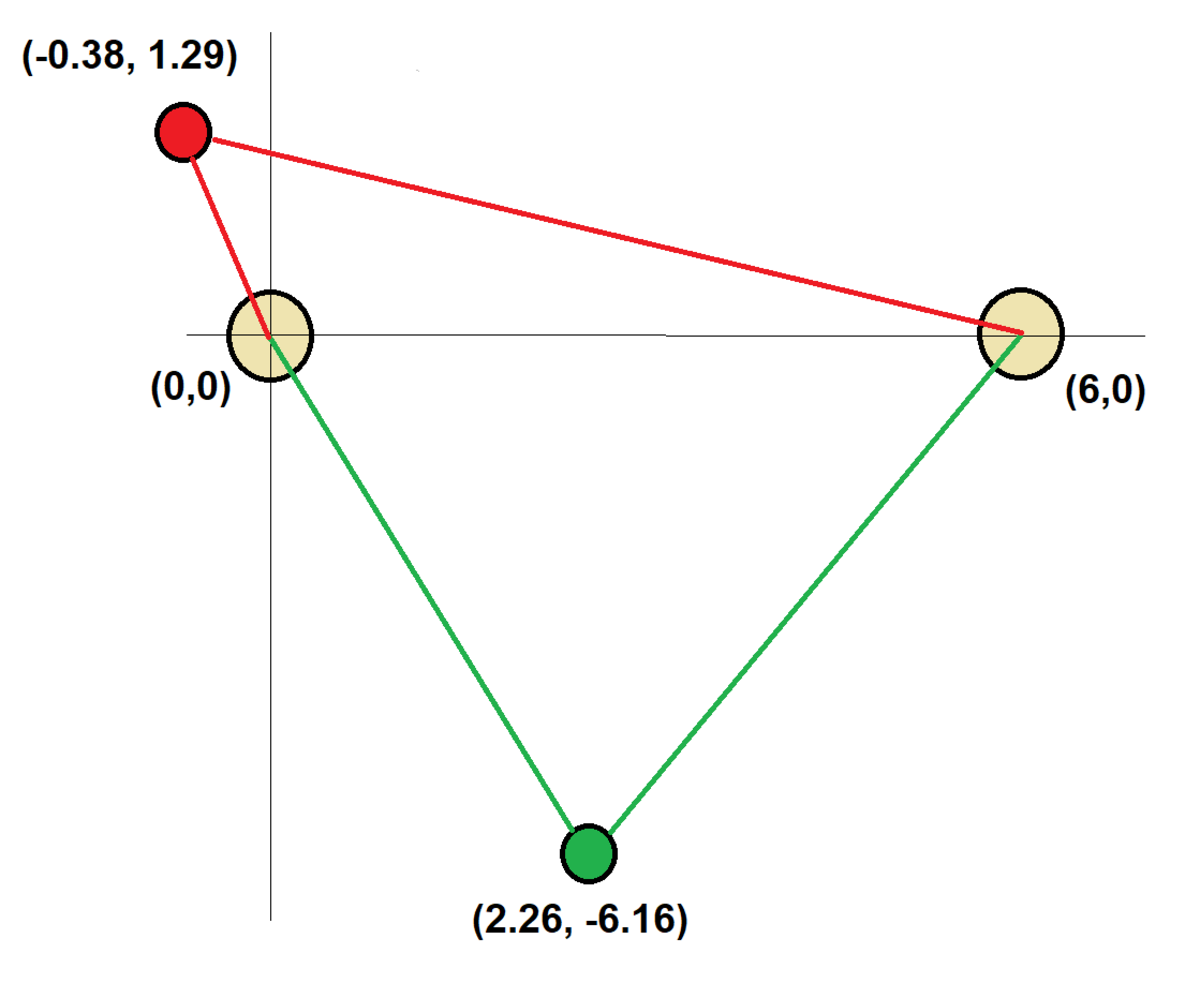
I used a hill-climbing algorithm to solve. Let the unknown coordinates be ( x , y ) . Randomly search the parameter space by introducing mutations. If the net force on the mass is smaller than the smallest seen so far, accept the mutations. If not, reject them. Eventually, the algorithm finds a point at which the net force is zero.
Interestingly, there are two equilibrium points, shown in the attached diagram. This problem asks for the stable equilibrium (shown in green). If the mass is perturbed starting at that point, it will eventually return. There is also an unstable equilibrium point, shown in red. Perturbing the mass in that state will result in the mass moving away and settling at the stable equilibrium point.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
|
Like your program. I wrote one but it keeps running out of execution time so I need to figure that out. Gonna look over your programming skills and see if I can learn some techniques tomorrow. Take care!
FYI - for ODE the methods used for solving are varied - Adams-Bashford, Runge-Kutta, Backward-differentiation, Radau, Burlisch-Stoer. Rosenbrock are some.
Do you know what method the "find" function uses to solve?
Log in to reply
Turns out they're pretty tight lipped about the exacts of what numerical methods are being used. You'd think it would be an easy answer to obtain. All I keep coming across are tutorials about how to use Mathcad but not why you should use as opposed to other more direct solutions like programming. I've had my frustrations with Mathcad, i.e. the other day I tried to solve an integral in that detention tank problem. It solved the 1st integral but got hung up in never, never land on the 2nd one. The trade off is you get lazy because it makes it easy for most problems, then you get rusty for more complex problems that only programming can solve. I'll keep looking and let you know. Probably just best to ask them directly which I'll do.
Log in to reply
I bet Mathcad will find the other point too if you modify the initialization. Of course, it is clear from the problem statement that we are supposed to find the stable equilibrium
Log in to reply
@Steven Chase – I put x=(-2.0) and y=2.0 as initial guess values and it gave the same result. Look into later....
I used Mathcad too, but because I only have "free" capability, I have to do things the hard way. As a result, I made some trivial errors in linearizing the system. Bummer! That was a much tougher problem than I initially suspected.
Nice Problem Joe!
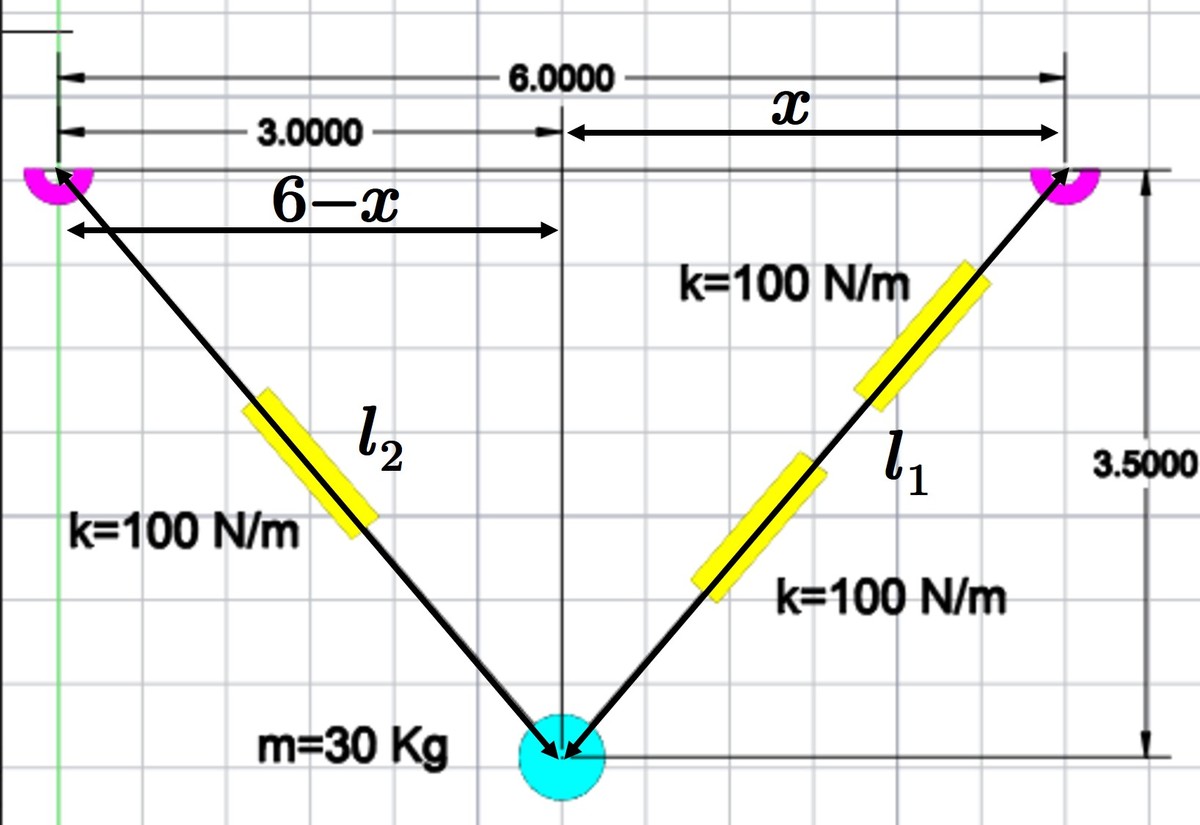

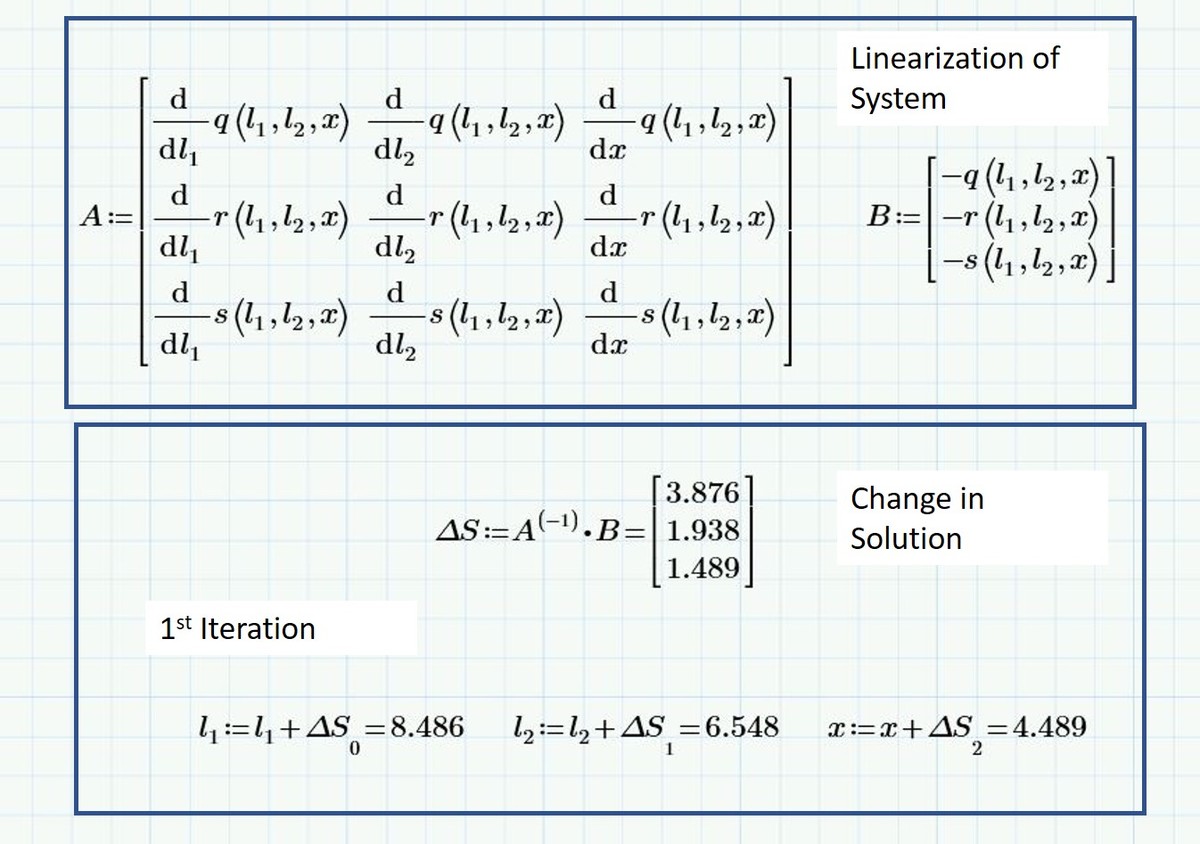

Thanks, Eric! Nice work. Like your skill with Mathcad.
Log in to reply
Thanks Joe... Now if I could only get better at figuring out my methodological errors before I've used up 3 tries! Oh, well...
Log in to reply
It happens. If we didn't make mistakes there would be no QA/QC departments.

The approach of my choice is the minimization of the potential energy of the mass.
Let the general coordinates of the mass be ( x , y ).
The potential energy of the mass is then:
V = m g y + 2 1 0 0 ( x 2 + y 2 − L ) 2 + 2 5 0 ( ( 6 − x ) 2 + y 2 − L ) 2
At stable equilibrium, the potential energy is globally minimized. The point at which this takes place is then used to compute the required answer. One can solve this by computing partial derivatives and using Newton-Raphson, however, I chose a brute force approach of parameter space sweeping.