Matching Areas

With the coordinates of point $P$ being $(a,2a^{2})$ we have that $A = \displaystyle\int_{0}^{a} (2x^{2} - x^{2}) dx = \left(\dfrac{1}{3}x^{3}\right)_{0}^{a} = \dfrac{1}{3}a^{3}$ .

Now, taking a more general approach, let curve $C$ be $y = f(x)$ . (We will show that $f(x)$ is necessarily a quadratic.) To calculate $B$ , we integrate with respect to $y$ :

$\displaystyle B = \int_{0}^{2a^{2}} \left(\sqrt{\dfrac{y}{2}} - f^{-1}(y)\right) dy = \dfrac{4}{3}a^{3} - \int_{0}^{2a^{2}} f^{-1}(y) dy$ .

Equating $A$ to $B$ we then find that $\displaystyle\int_{0}^{2a^{2}} f^{-1}(y) dy = a^{3}$ .

Next, using the Fundamental Theorem of Calculus, along with the observation that $f^{-1}(0) = 0$ by necessity, we differentiate to find that

$4a \times f^{-1}(2a^{2}) = 3a^{2} \Longrightarrow f^{-1}(2a^{2}) = \dfrac{3}{4}a \Longrightarrow 2a^{2} = f\left(\dfrac{3}{4}a\right)$ .

Letting $x = \dfrac{3}{4}a$ , we have that $a = \dfrac{4}{3}x \Longrightarrow 2a^{2} = \dfrac{32}{9}x^{2} \Longrightarrow f(x) = \dfrac{32}{9}x^{2}$ .

That is, curve $C$ is uniquely quadratic, with $f(12) = \dfrac{32}{9} \times 12^{2} = \boxed{512}$ .

Orange curve:

$y = x^2 \\ x = \sqrt{y}$

Red curve:

$y = 2 x^2 \\ x = \sqrt{\frac{y}{2}} = \frac{1}{\sqrt{2}} y^{1/2}$

Blue curve:

$y = \alpha x^2 \\ x = \sqrt{\frac{y}{\alpha}} = \frac{1}{\sqrt{\alpha}} y^{1/2}$

Red Area (A):

$A = \int_0^a (2 x^2 - x^2) dx = \frac{a^3}{3}$

Blue Area (B):

$B = \int_0^{2a^2} (\frac{1}{\sqrt{2}} y^{1/2} - \frac{1}{\sqrt{\alpha}} y^{1/2} ) dy = (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{\alpha}}) \int_0^{2a^2} y^{1/2} dy \\ = \frac{2}{3} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{\alpha}}) \sqrt{8} a^3$

Equate the two areas:

$\frac{a^3}{3} = \frac{2}{3} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{\alpha}}) \sqrt{8} a^3 \\ 1 = 2 (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{\alpha}}) 2 \sqrt{2} \\ \frac{1}{4} = 1 - \sqrt{\frac{2}{\alpha}} \\ \frac{2}{\alpha} = \frac{9}{16} \\ \alpha = \frac{32}{9}$

Evaluating the previously unknown curve at $x = 12$ gives:

$\frac{32}{9} (144) = 32(16) =\boxed{512}$

The coordinates of point P are $(x,2x^{2})$ .

The area A is therefore (as can be seen in other answers) $\frac{1}{3} x^{3}$ .

Then we notice that the integrals for B would be much easier if we considered the curves as functions of the $y$ axis, instead.

we define $x=g(y)$ to be the inverse of the requested function $f(x)$ .

The red curve is then $a(y)=\sqrt{\frac{y}{2}}$ .

The area A, translated to a function of $y$ is now $\frac{1}{3} \sqrt{\frac{y}{2}}^{3}$

The area B is the integral of the $a(y)$ function between 0 and y, minus the integral of $g(y)$ in the same range, which we'll call area C (that is the area between the blue curve and the y axis, in the drawing).

As we've defined, the area B+C is equal to $\int _{ 0 }^{ y }{ \sqrt { \frac { t }{ 2 } } dt } =\sqrt { \frac { 1 }{ 2 } } \frac { 2 }{ 3 } \sqrt { y } ^{ 3 }$ .

As A = B, the area C is equal to $C=(B+C)-B=\sqrt { \frac { 1 }{ 2 } } \frac { 2 }{ 3 } \sqrt { y } ^{ 3 }-\frac { 1 }{ 3 } \sqrt { \frac { y }{ 2 } } ^{ 3 }=\sqrt { \frac { 1 }{ 2 } } \frac { 1 }{ 2 } \sqrt { y } ^{ 3 }$ . We'll recall that this area is equal to the integral of $g(y)$ over the range.

Differentiating this expression to receive $x=g(y)$ is easy, and gives us $x=\frac { 3 }{ 2 } \sqrt { \frac { y }{ 8 } }$ .

Transforming this function back to the original axis gives us the requested function $f(x)=\frac { 32 }{ 9 } x^{2}$ .

From here, substituting $f(12)=\frac { 144 \times 32}{ 9 } = 512$

Change $x$ by $\Delta x$ and calculate the increment of the red area:

$A_1= \Delta x (2x^2-x^2)= \Delta x x^2$

Let us assume that at this value of $y$ the argument of the $f(x)$ function is $x=x_1$ . In other words, $f(x_1)=y$ . The increment of the blue area is:

$A_2=\Delta y (x-x_1)= \frac {d y}{d x} \Delta x (x-x_1)= 4x(x-x_1) \Delta x$

Making $A_1=A_2$ and solving for $x$ we get:

$x= \frac {4}{3} x_1$ .

If $x_1=12$ , we get $x=16$ and $y=512$

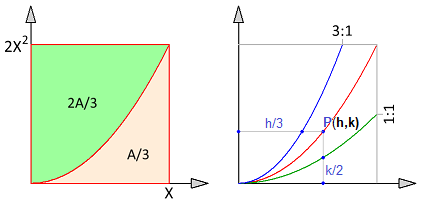
Area of the rectangle = $2X^3$

The area under the curve $y = 2x^2$ is $\frac{2X^3}{3}$ i.e. one third the area of the rectangle. So the area between $y = 2x^2$ and the Y axis must be two-thirds of the rectangle's area.

The curve $y = x^2$ divides every vertical line (ordinate of $y = 2x^2$ ) into two parts! So it must divide the area too into two equal halves.

So to get equal area, every horizontal line from Y axis to $y = 2x^2$ must be divided into ratio 3:1 by the unknown curve.

Writing $y = 2x^2$ as $x = \sqrt{\frac{y}{2}}$ and dividing the x coordinate in 3:1 gives $x = \frac{3}{4} \sqrt{\frac{y}{2}}$ which gives $f(x) = y = \frac{32}{9}x^2$

Giving f(12) = 512