Matchstick problem - 1
 If six matchsticks are given to you, then what is the maximum number of equilateral triangles you can make by connecting them?
If six matchsticks are given to you, then what is the maximum number of equilateral triangles you can make by connecting them?
Details and Assumptions :
-
You must connect the matchsticks only by their endpoints.
-
You can't break the matchsticks.
-
All of the matchsticks are of same size.
Check out Matchstick Problem - 2 .
Image Credit: Flickr Joel Fernandes .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
We can form 4 equilateral triangles by building a unit tetrahedron.
We would need at least 7 matchsticks for one matchstick to be part of three triangles. Therefore, each matchstick is part of at most 2 triangles, so the number of triangles is bounded above by 6 ⋅ 2 / 3 = 4 . Thus, 4 is the maximum number of equilateral triangles we can form with 6 matchsticks and the given rules.
Yes, the answer is regular tetrahedron. You just have to think in 3 dimensions.
But I didn't get your "at least 7 matchsticks" part.
Log in to reply
If one matchstick is part of three equilateral triangles, then any two of those triangles cannot share another edge, or else the triangles would coincide and share all three edges. Therefore, the three triangles together are formed from 7 matchsticks (1 shared and 2 more for each triangle).
Log in to reply
But, there is not any edge in a tetrahedron which shares 3 triangles. What is the necessity of mentioning this fact in your answer?
Log in to reply
@Md Omur Faruque – I needed to prove that 4 actually was an upper bound. First I showed any configuration had at most two triangles sharing any matchstick, then used that to show I couldn't get more than 4 triangles. Therefore 4 is an upper bound, and the tetrahedron shows that 4 is actually achievable, so the answer is 4 .
Log in to reply
@Maggie Miller – Got you now. The problem was you said you need at least 7 matchsticks but you didn't say anything about when you need them.
It would be better if you rephrase the solution to, "If a matchstick is part of three triangles, then we need at least 7 matchsticks. "
Log in to reply
@Md Omur Faruque – Oh, I see the problem - I type solutions on my phone, and autocorrect changed the word "three" to "the.' I fixed it - sorry for not noticing before!
How about a Star of David? Doesn't that have 8? One small one at each point and the 2 large ones.
Ah. Connected by endpoints only. Read the question!
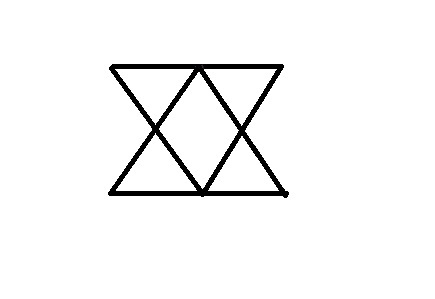
There is actually another way to do this. Each line in the image represents a matchstick of the same length. Although the configuration is two-dimensional, all the rules presented are obeyed, since all matchsticks are connected to their endpoints. The triangles formed are all equilateral and their sides are half as long as the original ones. Another way to visualize this is to make two equilateral triangles out of the six matchsticks and start moving the one towards the other until they match, as in the picture.
The rule is "....... only by their endpoints."
In the picture above, the matchsticks are also connected to the midpoint of another matchstick.
By the way, it has 6 triangles rather than 4.
Log in to reply
The star of David configuration produces 6 triangles.
Log in to reply
It actually produces 8 if you count the large triangles in the star of David, that was my answer, I understand why it was wrong now but I was pretty confident in it when I first saw the problem!
Log in to reply
@Garrett Clarke – 4 small & 2 large, I can see only 6 in total. Where are the 2 others?
Log in to reply
@Md Omur Faruque – No not in the image above, in the Star of David .
My answer is 8.
Make a star by creating 2 triangles.
In the given condition we can't form more than 2 triangles in 2 dimensions. In three dimensions, we can form a regular tetrahedron or triangular prism with exactly six matchsticks as the picture below (It's funny that we can't form 3 triangles):
So, the maximum possible triangles will be 4 .