Matchstick Problem - 2

If six matchsticks are given to you, then what is the maximum number of equilateral triangle you can make by connecting them?
Details and Assumptions :
-
You are n o t bound to connect the matchsticks only by their endpoints.
-
You can't break the matchsticks.
-
All of the matchsticks are of same size.
Check out Matchstick Problem - 3
Image Credit: Flickr Joel Fernandes .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
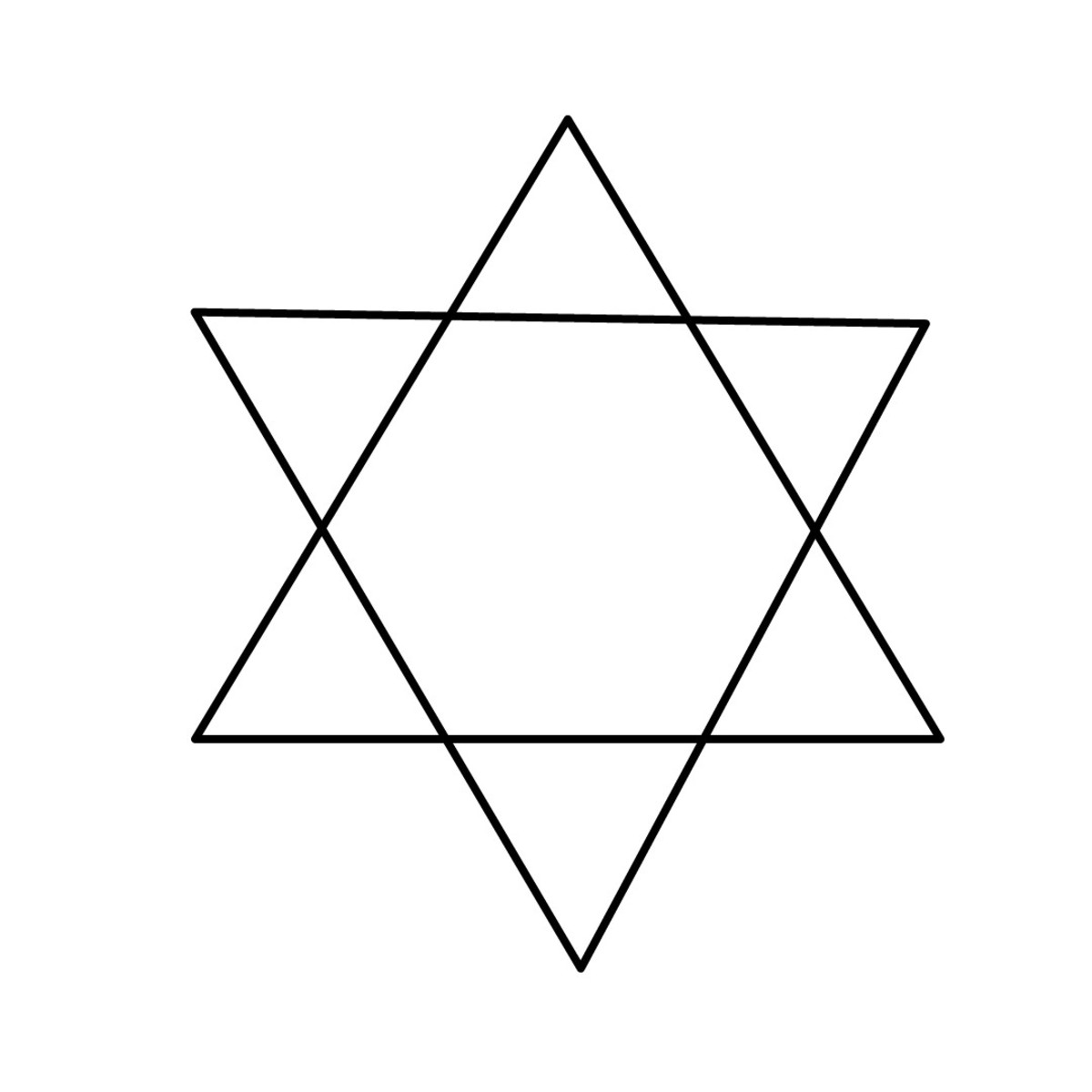
How can one show that 8 is the maximum?
Log in to reply
i have seen the same problem posted by someone else before
Log in to reply
I'm sorry if it's a repetition. But it's not a copy.
Log in to reply
@Md Omur Faruque – may be the other one is a copy
Log in to reply
@Akash Singh – I suspect you are thinking of his first problem ?
Log in to reply
@Calvin Lin – no
i had that one wrong (its solution says about the same six-pointed star)
so this i got correct
It's possible to make 8 equilateral triangles. I will show that we can't make >8.
Draw any old line and call it the x-axis. We can group the matchsticks into classes based on which of the intervals [ 0 , 3 2 π ) , [ 3 2 π , 3 4 π ) , [ 3 4 π , 2 π ) the angle they make with the x axis falls into . Let the number of matchstick in each class be a 1 , a 2 , a 3 . Any equilateral triangle must have one side from each class. So the number of equilateral triangles is at most a 1 a 2 a 3 ≤ ( 3 a 1 + a 2 + a 3 ) 3 = ( 3 6 ) 3 = 8 (by AM-GM).