Math Series #10
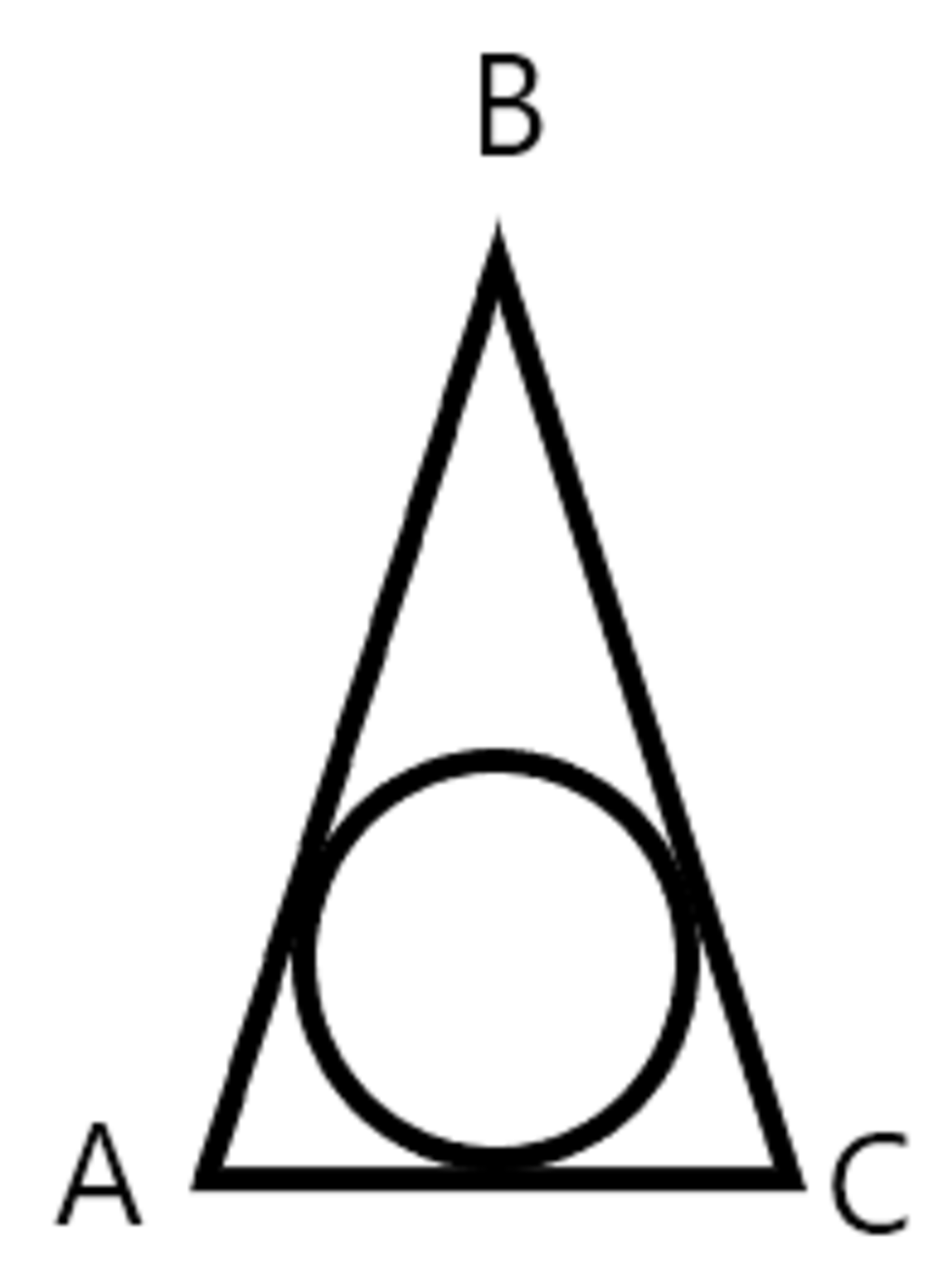 A circle is circumscribed by an isoscles triangle, where
A
B
=
B
C
=
6
cm and
A
C
=
4
cm. Find the area of the circle.
(
π
=
3
.
1
4
)
A circle is circumscribed by an isoscles triangle, where
A
B
=
B
C
=
6
cm and
A
C
=
4
cm. Find the area of the circle.
(
π
=
3
.
1
4
)
The answer is 6.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Avner Lim - You should change the wording to B A = B C = 6 and A C = 4 in order to correspond to to the figure.
Log in to reply
Hmm, but that A C looks smaller than B C and A B . And B C and A B looks same. But I will change that. It will be far more better if you do change the question statement. ;)
Log in to reply
Sorry, my comment was addressed to the problem author, @Anver Lim, not to your solution which is OK. This is what I'm suggesting too, that he changes the question statement.
Thanks @Thanos Petropoulos for mentioning it. I have fixed it.
let A T = area of the triangle , R C = radius of the incircle , A C = area of the incircle and P T = perimeter of the triangle
Compute the area of the triangle using the Heron's Formula :
s = 2 a + b + c = 2 6 + 6 + 4 = 8
A T = s ( s − a ) ( s − b ) ( s − c ) = 8 ( 8 − 6 ) ( 8 − 6 ) ( 8 − 4 ) = 8 2
Compute the radius of the incircle using a formula:
R C = P T 2 ∗ A T = 6 + 6 + 4 2 ∗ 8 2 = 2
Compute the area of incircle:
A C = π ∗ R 2 = 3 . 1 4 ( 2 ) 2 = 6 . 2 8
A M and A O are two tangents from Point A ,so A O = A M (see figure)
∆ A O B is a right angled triangle . So A O 2 + B O 2 = A B 2 ⟹ B O = A B 2 − A O 2 = 6 2 − 2 2 = 4 2 c m
Now tangents are perpendicular to radius of the circle . So ∆ M P B is a right angled triangle .Here B P = 4 2 − r ( r =Radius of the circle)
So , M B 2 + M P 2 = P B 2 ⟹ 4 2 + r 2 = ( 4 2 − r ) 2 ⟹ r = 2 c m
Area of the circle π ( 2 ) 2 = 2 π ≈ 6 . 2 8 c m 2