Mathathon 2020 − Problem 1 (Easy)
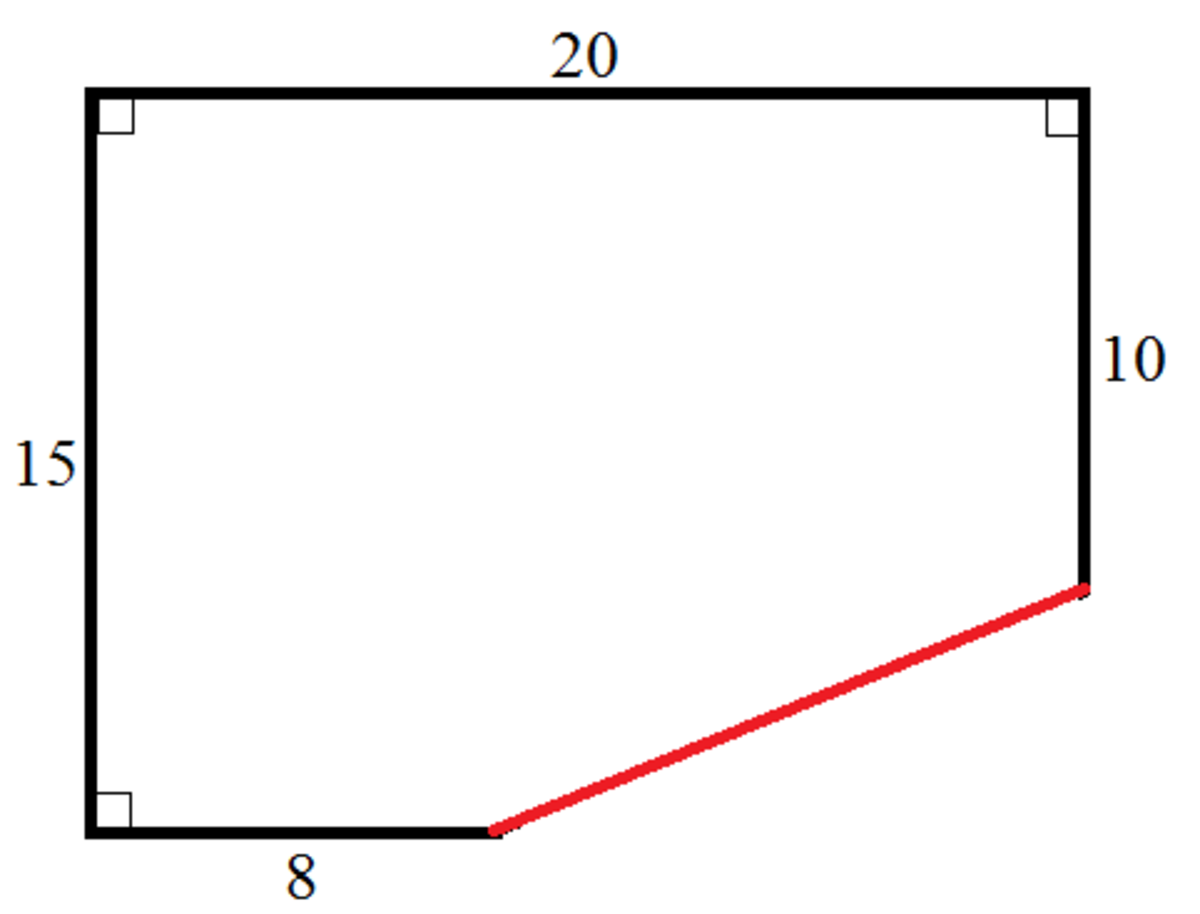
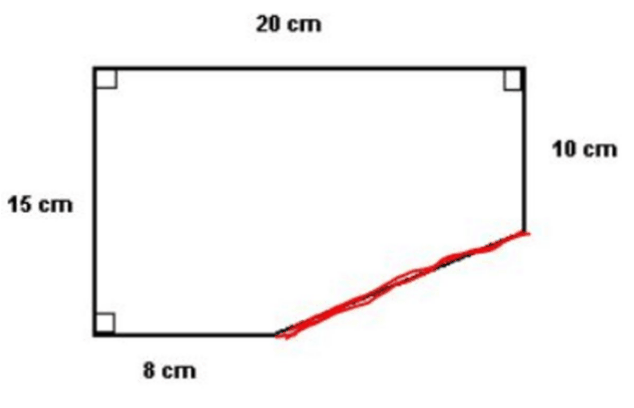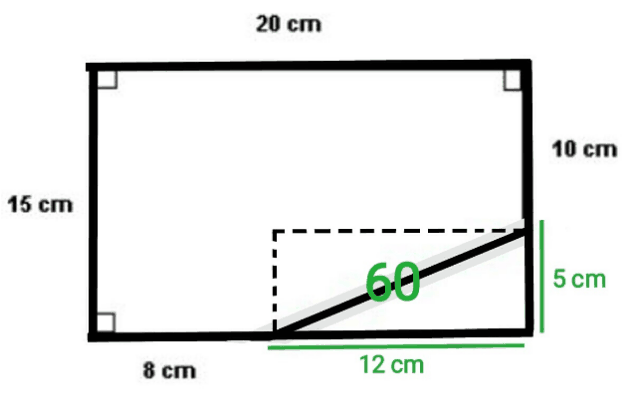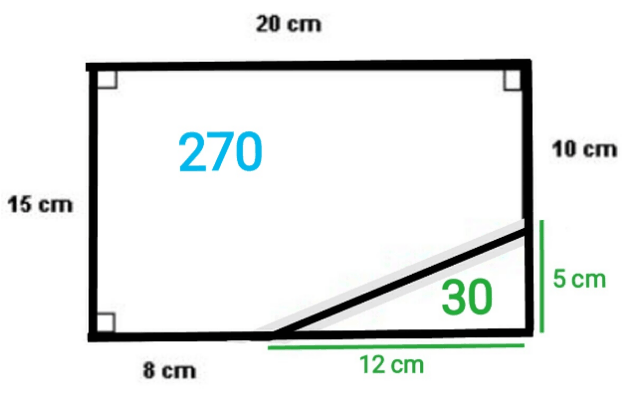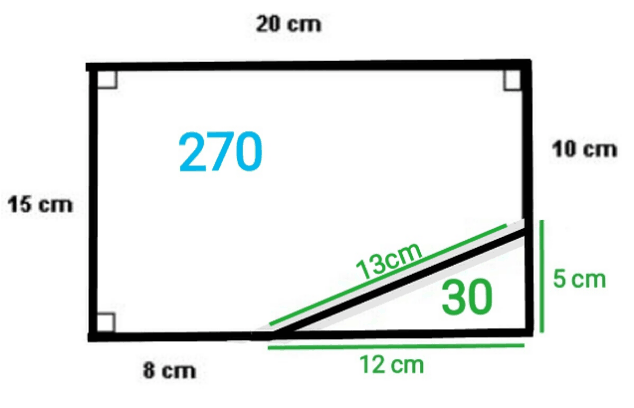
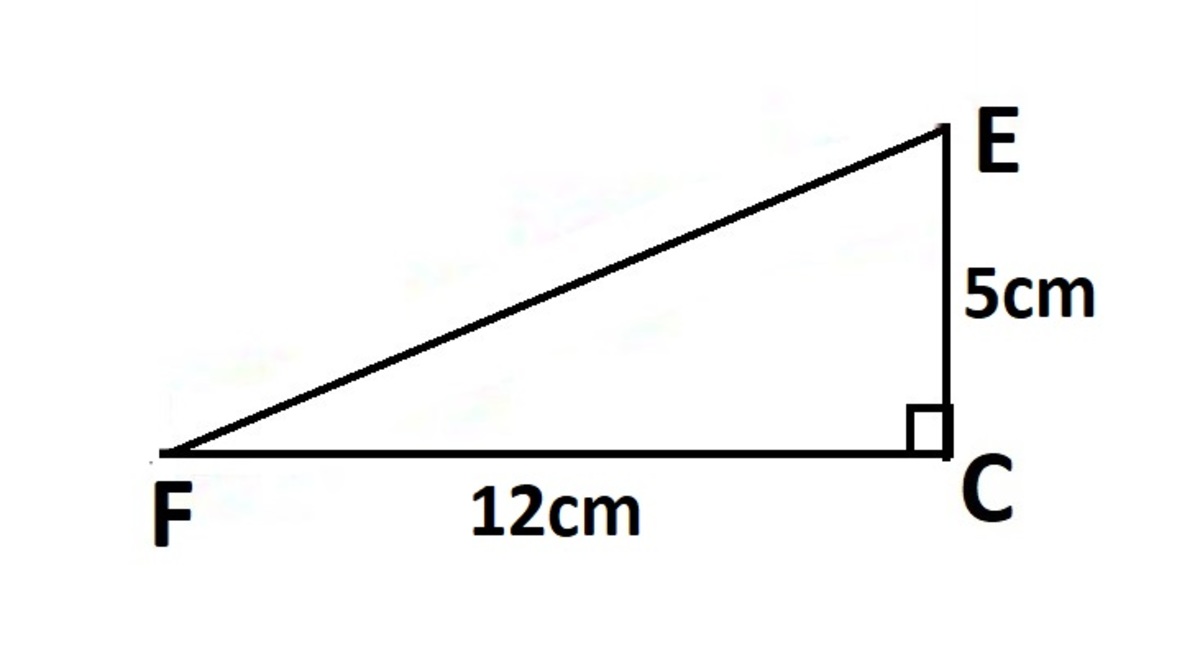
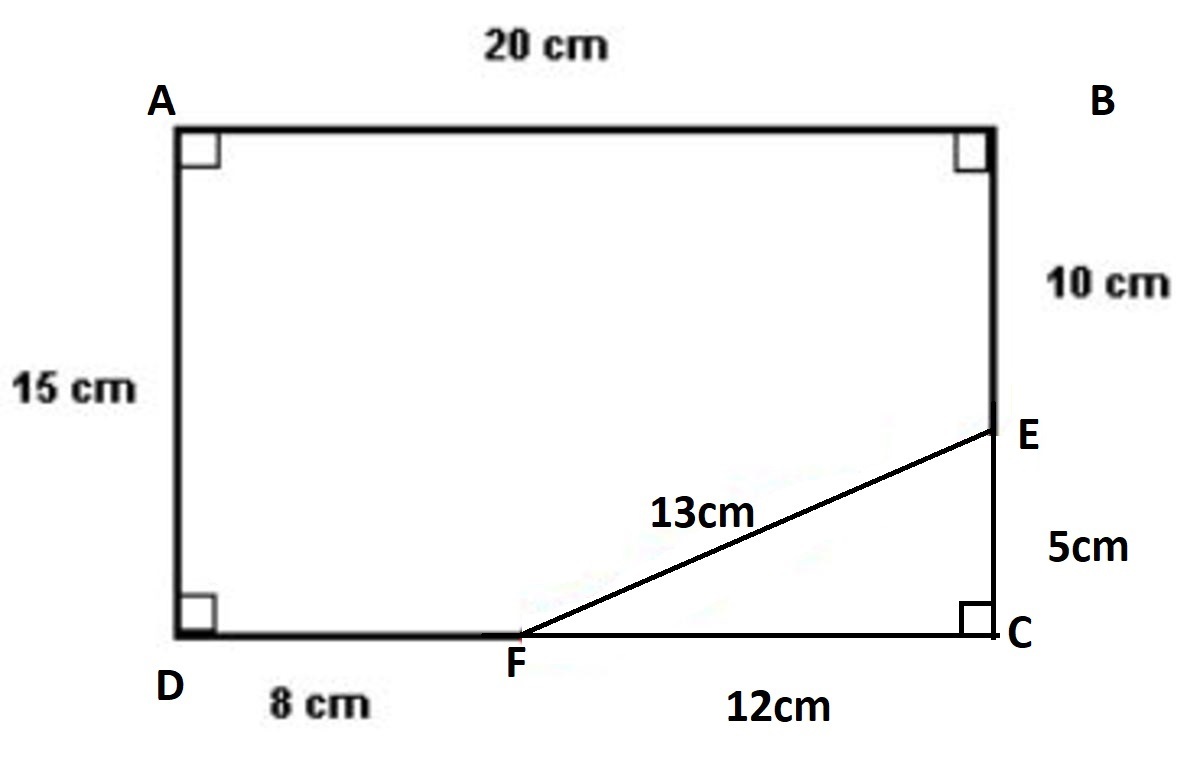
The figure shows a rectangle with a right triangle being cut out and the remaining area is x . If The length of the red line is y . What is x + y .
Note: This is an actual contest question and your solutions shall be evaluated by me.
The answer is 283.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions

| Uniqueness | 10 | Nobody actually broke it into smaller shapes, nice! |
| Latex | 10 | Cool GIF |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 10 | The beautiful GIF explains everything very nicely |
| Time | 9 | Second solution |
| @Mahdi Raza 's Total | 49 | Almost perfect! |
Log in to reply
Ok, Maybe I can participate, add me back in. Thanks!
Log in to reply
Of course, you're back in! Great GIF, i love it @Mahdi Raza
Wow, points for Latex are given even though its an animation! Keep it up @Percy Jackson
Log in to reply
If you're not mocking me - Thank you, If you are mocking me - Thank you, because Animation's and pics are part of Latex in this contest, so Latex domain is like aesthetics domain actually :) #Persassy
Log in to reply
@A Former Brilliant Member – Ok, it is your contest anyways. I am writing my solution tho.
2 more Mathathon problems are available, try those out too @Mahdi Raza
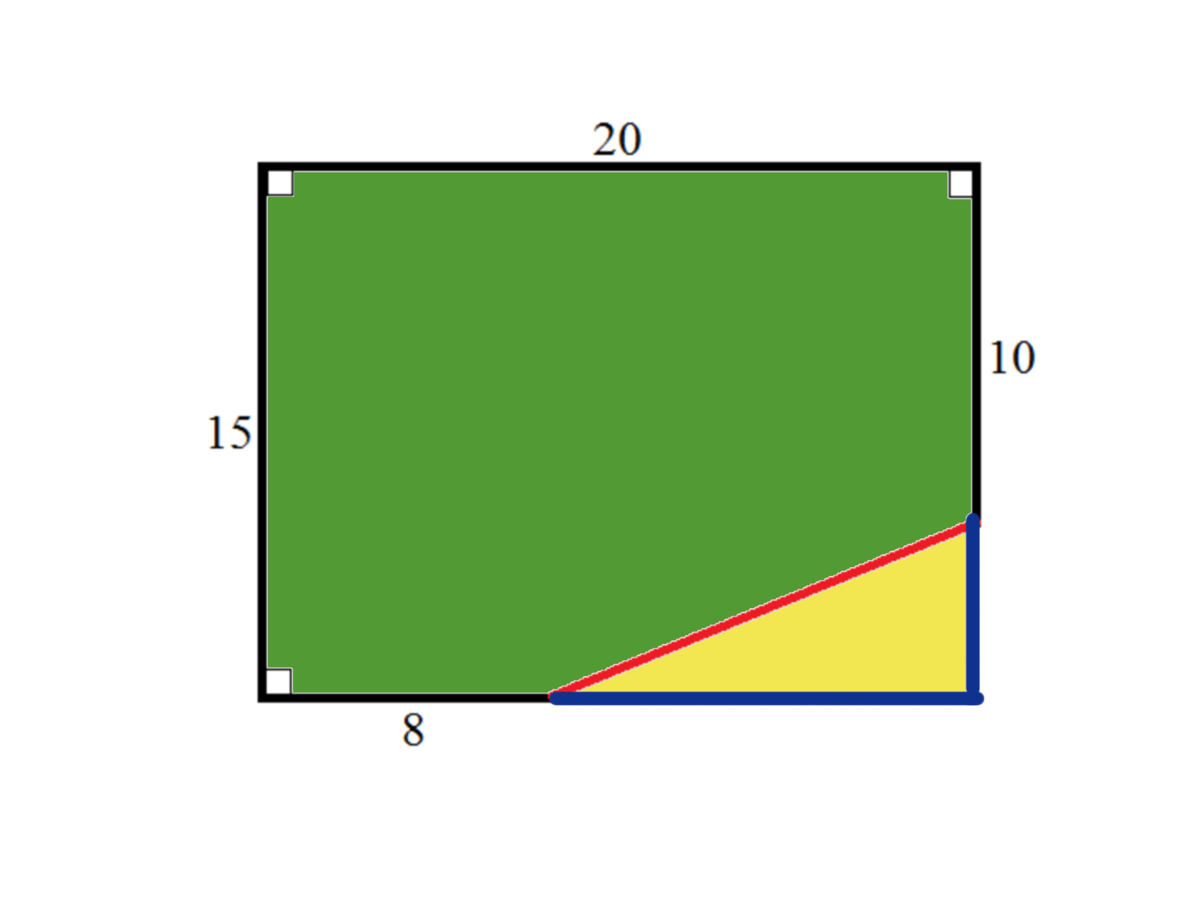
The total area
The yellow area and the green area equals to the entire area of the rectangle.
As the length and the width are both 15 and 20, and the area is the length and width multiplied, the total area is 300.
The red line
To find the length of the red line, we need to square the horizontal blue line’s length and add it to the square of the vertical blue line’s length. The length can be calculated by taking 8 away from 20, and 10 away from 15. If you square both the numbers, you get 144 (12 squared) and 25 (5 squared). Adding these together equals 169, which if you find the square root of, is 13. This shows that the red line is 13.
The green space
To find the area of the green space, we must take the yellow space away from the total. As I have said, the length and width of the triangle is 12 and 5, respectively. Finding the area, we multiply them together and divide by two. This gives us 30.
The total area has been mentioned above (300), so subtracting 30 from 300 equals 270. This is the green space’s area.
The final step
The question states that we need to add x and y. We have found the values of both (270 and 13), so the last thing to do is add them together.
270 + 13 = 283
O u r a n s w e r i s 2 8 3
Uh...Sarah, this is the 2020 Mathathon. You should be solving the 2021 problems...
Log in to reply
What? I guess I didn’t read it properly. READ THE TITLE, SARAH! Sorry.
Log in to reply
lmao no problem, you have plenty of time to solve the others...and I have a few days to score hundreds of solutions...lol
Everyone, please don't delete solutions as it will confuse me and the Mathathon scoring system will be destroyed!!!!!!!!!!!!!!!!
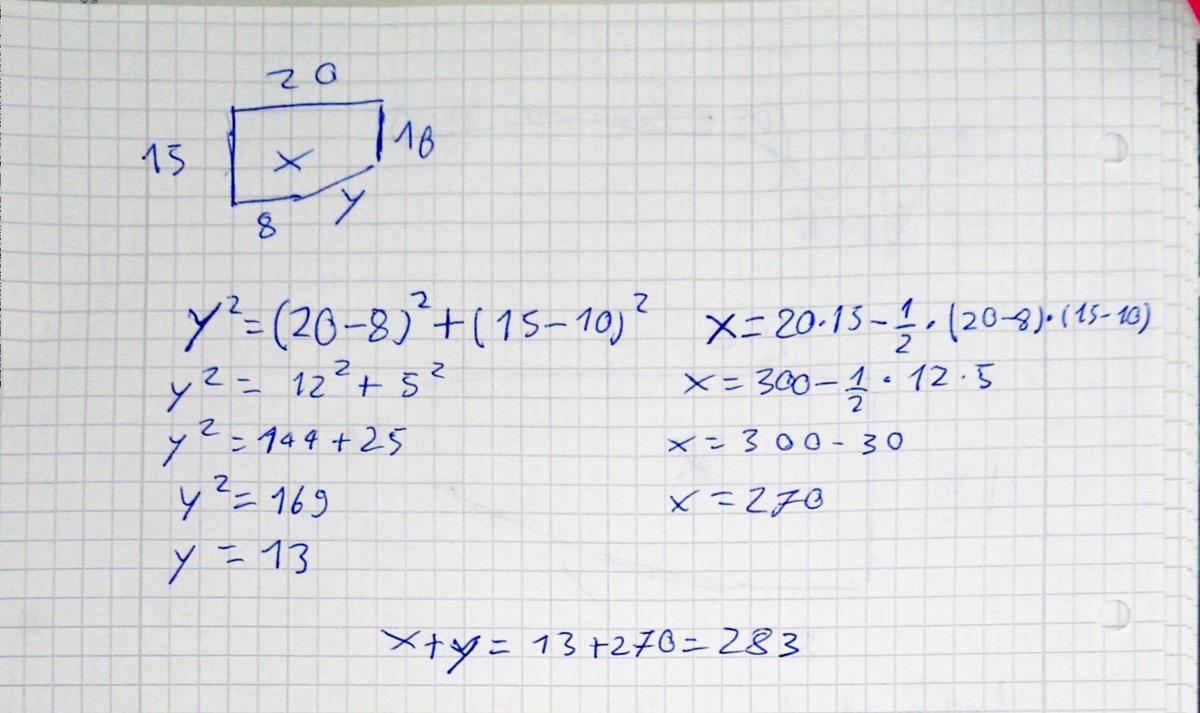
Btw. there is no Latex used in this one ....
| Uniqueness | 0 | Common approach |
| Latex | 0 | You know why...... |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 5 | The solution isn't very clear due to everything being written with pen |
| Time | 0 | 11th solution |
| @Lorenz W. 's Total | 15 | Try using Latex next time! |
@Elijah L mention[3990831:Elijah L]
As your name is hard to find, I'm making this mention, ask @Hamza Anushath and her note for more info
To figure out x, We split the shape into two parts. One part would be are rectangle. The other will be a trapezium. The dimensions of the rectangle is the height of it is 10 and the width is 20. The dimensions of the trapezium is that its height would be 15-10=5 and the two lengths of it would be 20 and 8.
This means the area of the shape, x, we add the area of the rectangle and the trapezium together. 10 * 20 + 5 * (20 + 8) / 2 = 200 + 70 = 270
So, the value of x is equal to 270.
To figure out y, We identify if we join up the sides of the rectangle into a corner it would be rectangle. Therefore, the triangle we have made by connecting the last bits of the sides is a right-angled one. We already have the height which is 15-10=5 and the base is 20-8=12. Therefore, we have the dimensions of the right-angled triangle other than the hypotenuse.
We calculate y, which is the hypotenuse of the triangle using the Pythagoras Theorem, a^2 + b^2 = y^2 This is where a and b are the sides of the triangle expect the hypotenuse. a = 12 and b = 5. We substitute. 12^2 + 5^2 = y^2 144 + 25 = y^2 169 = y^2 y = 13
x + y = 270 + 13 = 283
Therefore, the answer is 283.
I'm ready for score
| Uniqueness | 3 | Nobody used trapezium area |
| Latex | 0 | You know why...... |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 5 | The solution isn't very clearly explained |
| Time | 1 | 10th solution |
| @Feng Li 's Total | 19 | Try using Latex next time1 |
Therefore, the final answer should be 2 7 0 + 1 3 = 2 8 3
Gah!!!!! Now I know why you shouldn't sleep with your phone on, so many notifications! LOL XD Nice solution, I'll score it tom morning, or maybe now :)
| Uniqueness | 0 | common approach |
| Latex | 10 | Cool GIF and La-text |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 10 | The great GIF explains everything very nicely |
| Time | 3 | 8th solution |
| @Hamza Anushath 's Total | 33 | Great job! |
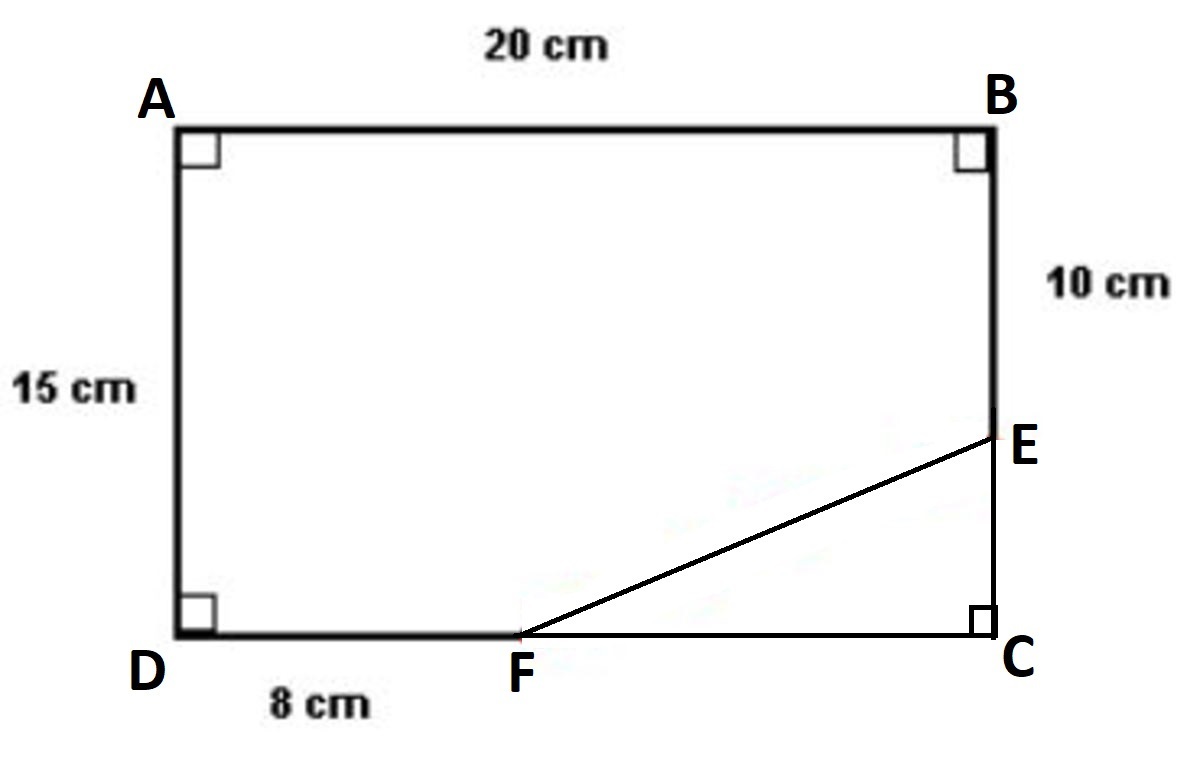
Completing the figure first.
We will draw the complete rectangle again, by bringing the cutout piece back and label the figure accordingly:
Image not to scale
Calculating the length of y.
We will use the above image and solve for y, where y=XY. In the above image, C X ⊥ C Y as they are part of segments of a rectangle, so they are perpendicular.
Thus, △ X C Y is a right-angle triangle. We can now use Pythagoras theorem to find the length of XY.
We have, X C 2 + Y C 2 = X Y 2
Substituting the length of XC and YC, we get, 5 2 + 1 2 2 = X Y 2
Solving further, 25 + 144 = 169 = X Y 2
Taking the positive square root on both sides, 1 6 9 = 13 = XY.
- Thus, the length of XY i.e y = 13
Solving for the area x.
We will again use the image above for reference, the area of the remaining part would be:
x = A r e a ( □ A B C D ) − A r e a ( △ X C Y )
x = 2 0 × 1 5 − 2 1 2 × 5 (As the length and breadth of the rectangle are 20 and 15, and the triangle's base is 12 and height is 5.)
x = 300-30
x = 270
Adding the values.
x + y = 270 + 13
Thus, x + y= 283
Im done @Percy Jackson
Log in to reply
@Percy Jackson when will you score me?
Log in to reply
Probably when I'm done sleeping bro, check the US time! @Siddharth Chakravarty
| Uniqueness | 0 | Same method as everyone else |
| Latex | 10 | Boxes, bolding and sizes, I have to give you a 10 |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 10 | The solution has been explained in a nice way |
| Time | 4 | 7th solution |
| @Siddharth Chakravarty 's Total | 34 | Good solution! |
 As
A
B
C
D
is a rectangle
∴
A
D
=
B
C
=
B
E
+
E
C
=
1
0
c
m
+
E
C
⇒
1
5
c
m
=
1
0
c
m
+
E
C
∵
A
D
=
1
5
c
m
⇒
E
C
=
1
5
c
m
−
1
0
c
m
=
5
(
3
)
c
m
−
5
(
2
)
c
m
=
5
(
3
−
2
)
c
m
=
5
(
1
)
c
m
=
5
c
m
∵
5
(
3
)
=
1
5
;
5
(
2
)
=
1
0
;
a
(
b
)
−
a
(
c
)
=
a
(
b
−
c
)
Similarly,
A
B
=
D
C
=
D
F
+
F
C
=
8
c
m
+
F
C
⇒
2
0
c
m
=
8
c
m
+
F
C
∵
A
B
=
2
0
c
m
⇒
F
C
=
2
0
c
m
−
8
c
m
=
4
(
5
)
c
m
−
4
(
2
)
c
m
=
4
(
5
−
2
)
c
m
=
4
(
3
)
c
m
=
1
2
c
m
∵
4
(
5
)
=
2
0
;
4
(
2
)
=
8
;
a
(
b
)
−
a
(
c
)
=
a
(
b
−
c
)
Also as
A
B
C
D
is a rectangle
∴
∠
E
C
F
=
2
1
π
=
9
0
°
As
A
B
C
D
is a rectangle
∴
A
D
=
B
C
=
B
E
+
E
C
=
1
0
c
m
+
E
C
⇒
1
5
c
m
=
1
0
c
m
+
E
C
∵
A
D
=
1
5
c
m
⇒
E
C
=
1
5
c
m
−
1
0
c
m
=
5
(
3
)
c
m
−
5
(
2
)
c
m
=
5
(
3
−
2
)
c
m
=
5
(
1
)
c
m
=
5
c
m
∵
5
(
3
)
=
1
5
;
5
(
2
)
=
1
0
;
a
(
b
)
−
a
(
c
)
=
a
(
b
−
c
)
Similarly,
A
B
=
D
C
=
D
F
+
F
C
=
8
c
m
+
F
C
⇒
2
0
c
m
=
8
c
m
+
F
C
∵
A
B
=
2
0
c
m
⇒
F
C
=
2
0
c
m
−
8
c
m
=
4
(
5
)
c
m
−
4
(
2
)
c
m
=
4
(
5
−
2
)
c
m
=
4
(
3
)
c
m
=
1
2
c
m
∵
4
(
5
)
=
2
0
;
4
(
2
)
=
8
;
a
(
b
)
−
a
(
c
)
=
a
(
b
−
c
)
Also as
A
B
C
D
is a rectangle
∴
∠
E
C
F
=
2
1
π
=
9
0
°
 ⇒
△
E
C
F
is right angled at vertex
C
∴
from
Pythagorean theorem
F
C
2
+
E
C
2
=
E
F
2
⇒
(
1
2
c
m
)
2
+
(
5
c
m
)
2
=
E
F
2
⇒
1
4
4
c
m
2
+
2
5
c
m
2
=
E
F
2
⇒
1
6
9
c
m
2
=
E
F
2
⇒
E
F
=
−
+
1
6
9
c
m
2
=
−
+
1
6
9
c
m
2
=
−
+
1
3
c
m
But as lengths are positive
∴
E
F
=
1
3
c
m
=
y
⇒
△
E
C
F
is right angled at vertex
C
∴
from
Pythagorean theorem
F
C
2
+
E
C
2
=
E
F
2
⇒
(
1
2
c
m
)
2
+
(
5
c
m
)
2
=
E
F
2
⇒
1
4
4
c
m
2
+
2
5
c
m
2
=
E
F
2
⇒
1
6
9
c
m
2
=
E
F
2
⇒
E
F
=
−
+
1
6
9
c
m
2
=
−
+
1
6
9
c
m
2
=
−
+
1
3
c
m
But as lengths are positive
∴
E
F
=
1
3
c
m
=
y
 Area of
A
B
C
D
=
B
A
S
E
×
H
E
I
G
H
T
=
2
0
c
m
×
1
5
c
m
=
1
0
×
2
×
1
.
5
×
1
0
c
m
2
=
1
0
0
×
3
=
3
0
0
c
m
2
Area of
A
B
C
D
=
B
A
S
E
×
H
E
I
G
H
T
=
2
0
c
m
×
1
5
c
m
=
1
0
×
2
×
1
.
5
×
1
0
c
m
2
=
1
0
0
×
3
=
3
0
0
c
m
2
Area of △ E C F = 2 1 B A S E × H E I G H T = 2 1 × 1 2 c m × 5 c m = 6 × 5 c m 2 = 3 × 2 × 5 c m 2 = 3 × 1 0 c m 2 = 3 0 c m 2
x = Area of A D F E B = Area of A B C D − Area of E F C = 3 0 0 c m 2 − 3 0 c m 2 = 3 0 × 1 0 2 c m 2 − 3 0 c m 2 = 3 0 ( 1 0 − 1 ) c m 2 = 3 0 ( 9 ) c m 2 = 2 7 0 c m 2
x + y = 2 7 0 c m 2 + 1 3 c m = 2 8 3
A problem!, we can't add c m 2 to c m !
I meant the value of x + y, not the units, but I'll change that anyway!
Log in to reply
You may write like this let the area of A D F E B = x c m 2 and let length of E F = y c m
| Uniqueness | 0 | common method of solving this problem |
| Latex | 10 | Good use of Latex for coloring! |
| No Mistakes | 9 | The last picture has 2 F points on the triangle |
| Clarity | 10 | Very clear solution! |
| Time | 6 | 5th solution |
| @Zakir Husain 's Total | 35 | Cool! |
First step: Use the
Pythagorean Theorem
to label the rectangle:
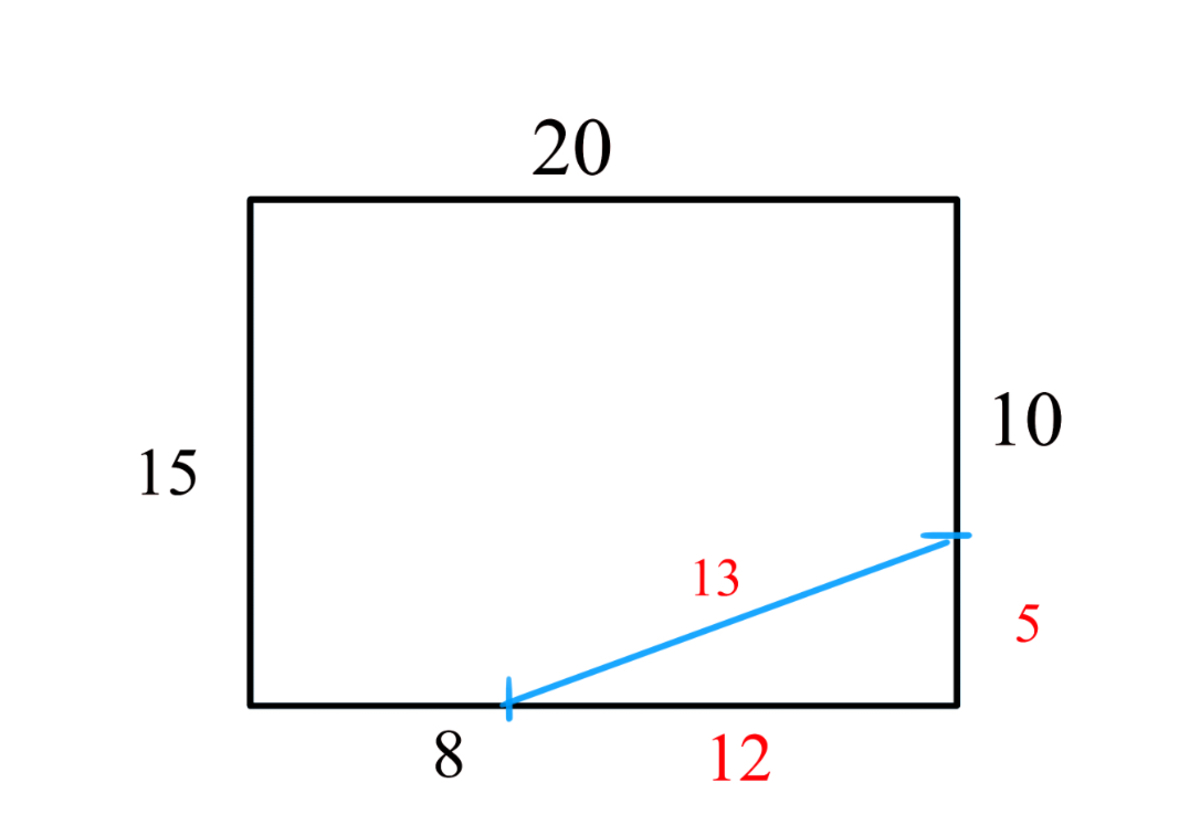 Identities:
2
0
−
8
=
1
2
,
1
5
−
1
0
=
5
,
5
2
+
1
2
2
=
1
3
Identities:
2
0
−
8
=
1
2
,
1
5
−
1
0
=
5
,
5
2
+
1
2
2
=
1
3
So
y
=
1
3
.
Now the rectangle’s area. This is given by
S
□
−
S
R
t
△
. So the area is
1
5
×
2
0
−
2
5
×
1
2
=
3
0
0
−
3
0
=
2
7
0
.
So the answer is
2
7
0
+
1
3
=
2
8
3
.
| Uniqueness | 0 | common approach |
| Latex | 10 | Good Latex-ing skills and color highlighting |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 10 | Picture and Equations are crystal clear |
| Time | 7 | 4th solution |
| @Jeff Giff 's Total | 37 | Good Job! |

y = 5 2 + 1 2 2
y = 2 5 + 1 4 4
y = 1 6 9
y = 1 3
x = ( 2 0 × 1 5 ) − ( 2 1 × 5 × 1 2 )
x = 3 0 0 − 3 0
x = 2 7 0
x + y = 2 7 0 + 1 3 = 2 8 3
Does anybody know how to give spacing in Latex? I wanted the x and y to be side by side but couldn't do it :(
| Uniqueness | 0 | common approach |
| Latex | 10 | Good Latex-ing skills |
| No Mistakes | 10 | The solution has no mistakes |
| Clarity | 10 | Picture and Equations are crystal clear |
| Time | 8 | Third solution |
| @Abhinandan Shrimal 's Total | 38 | Good Job! |
Log in to reply
You're so fast!
Log in to reply
I know right! @Abhinandan Shrimal
Log in to reply
@A Former Brilliant Member – Isn't it like midnight in USA right now?
Log in to reply
@Abhinandan Shrimal – I don't like sleeping, I get nightmares, as I am a demigod, but as a human I hate sleeping too. @Abhinandan Shrimal
Log in to reply
@A Former Brilliant Member – hahahhahahh heard you killed the minotaur? TWICE?
Log in to reply
@Abhinandan Shrimal – Yup, LOL, ol' beefy knows more than ever now to not mess with me..........
Your score in leaderboard has been updated @Abhinandan Shrimal
Notice that the original figure is a rectangle. This means that opposite sides are equal.
From this, we can deduce that the legs of the cut-out triangle are 5 and 1 2 . We know the triangle is right, so the hypotenuse is 1 3 . y = 1 3 .
The original area of the rectangle is 3 0 0 , and the area of the cut-out triangle is 2 5 × 1 2 = 3 0 . So the remaining area is 3 0 0 − 3 0 = 2 7 0 . x = 2 7 0 .
Then, x + y = 2 8 3 .
| Uniqueness | 0 | This is the common approach used by most people |
| Latex | 5 | Numbers are Latex-ed but the font could be more elegant |
| No Mistakes | 10 | No mistakes! |
| Clarity | 5 | Some things haven's been specified, like how you calculated the sides of the right triangle |
| Time | 10 | First Answer! Well done |
| @Elijah L 's Total | 30 | Well done! |
Log in to reply
Forgot about what the criteria were, I'll try to adapt to that next time.