Mathathon 2020 - Sample Problem 2

Unique strategy:

more traditional strategy:

$3t+7c =376 \cdots(1)$ $8t+2c=486\cdots(2)$

Subtract $(1)$ from $(2)$

$5t-5c=110$ $\implies t-c=22\dots(3)$

Multiply $(3)$ by $7$

$7t-7c=154\dots(4)$

Add $(1)$ and $(4)$

$10t=530$ $\implies \boxed{t=53}$

Put value of $t$ in $(3)$

$53-c=22$ $\implies \boxed{c=31}$

$\Large{c+t=53+31=\color{#D61F06}{\boxed{84}}}$

Let $c$ be the number of chairs and $t$ the number of tables.

$3t + 7c = \$376$ $(1)$

$8t + 2c = \$486$ $(2)$

Multiply $(1)$ by $8$ and $(2)$ by $3$ :

$24t + 56c = \$3008$ $(2)$

$24t + 6c = \$1458$ $(1)$

Now, subtract the two equations:

$56c - 6c = \$(3008 - 1458)$

$(56 - 6)c = \$(3008 - 1458)$

$(56 - 6)c = \$1550$

$50c = \$1550$

$\frac{50c}{50}$ $=$ $\frac{\$1550}{50}$

$c =$ $\frac{\$1550}{50}$

$c =$ $\frac{\$310}{10}$

$c =$ $\frac{\$31}{1}$

$c = \$31$ .

Therefore one chair costs $\fbox{\$31}$ .

Now substitute it into the unaltered first equation we used at the start:

$3t + 7c = \$376$

$3t + 7(\$31) = \$376$

$3t + \$217 = \$376$

$3t = \$(376 - 217)$

$3t = \$159$

$\frac{3t}{3}$ $=$ $\frac{\$159}{3}$

$t =$ $\frac{\$159}{3}$

$t =$ $\frac{\$53}{1}$

$t = \$53$

Therefore, one table costs $\fbox{\$53}$ .

In order to solve the question, we must give our answer in the form $c + t$ .

Therefore, when $c = \$31, t = \$53$ :

$\$(31 + 53) = \$83$

Therefore, the answer is $\rightarrow \fbox{\$83}$

There are two main ways of solving the problem.
1. Use a calculator to graph it out. Not suggested.

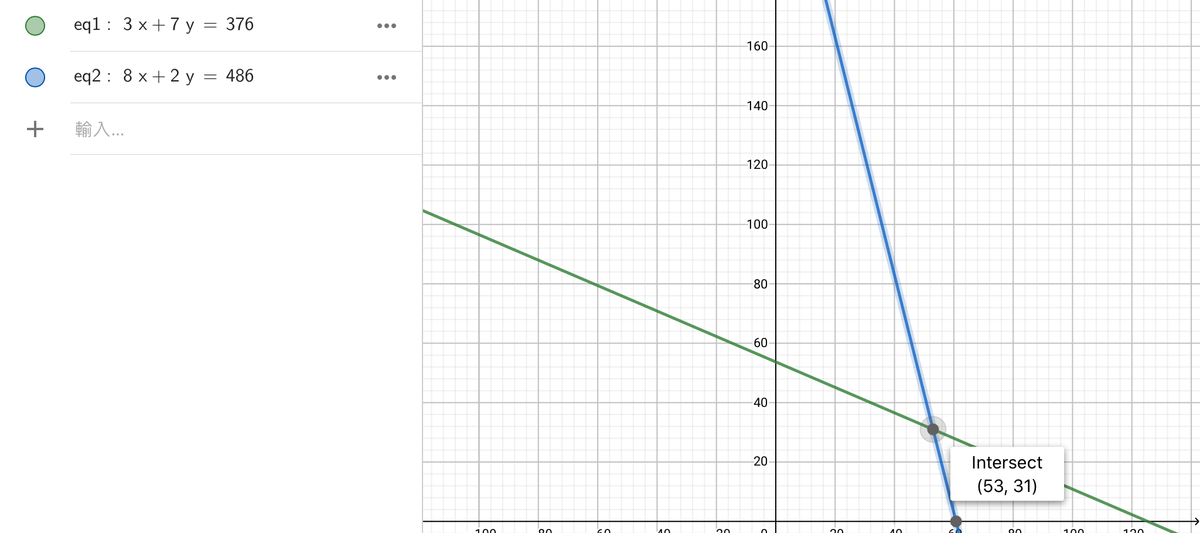
2. Solve the set of equations. Two ways. $\begin{cases} 3x+7y=376, (1)\\ 8x+2y=486. (2) \end{cases}$ A.
$(1)\times 8,(2)\times 3$ , so
$\begin{cases} 24x+56y=3008, (1’)\\ 24x+6y=1458. (2’) \end{cases}$ $(1’)-(2’)$ to eliminate $x$ :
$50y=1550,y=31$ .
Substitute: $3x+7\times 31=376,x=53.$
B.
$3x+7y=376,7y=376-3x, y=\frac{376-3x}{7}(1”).$
Now substitute $(1”)$ in $(2)$ .
$8x+\frac{2(376-3x)}{7}=486, 8x+\frac{752}{7}-\frac{6}{7}x=486, 7\frac{1}{7}x=378\frac{4}{7}.$ So $x=53$ , and we also arrive at $y=31$ .

Same as @Alak Bhattacharya 's solution $\\\alpha: 3t+7c = 376 \\\beta: 8t+2c = 486\\$ $\alpha\times2-\beta*7$ yields $-50t = -2650\\$ divide both sides by $-50$ yields $t = 53\\$ Put $t = 53$ into $\alpha\\$ We've got $3\times53+7c=376\\$ By moving terms, $7c=217\rightarrow c=31\\$ . Finally, the question asked for the sum of the costs of each table and chair? $\\\therefore\boxed{t+c}\rightarrow\boxed{53+31=84}$

Let the cost price of one table be $\$x$ and of one chair be $\$y$ . Then

$3x+7y=376$

$8x+2y=486$

Solving we get $x=53,y=31$ and the answer is $\boxed {\$53+\$31=\$84}$ .

By converting the sentences into algebraic equations, we can set up a system of equations in two variables, namely, the price of a table ( $t$ ) and the price of a chair ( $c$ ).

$\begin{cases} 3t+7c=376 \\ 8t+2c=486 \end{cases}$

Dividing both sides of the second equation by two yields:

$4t+c=243$

Subtracting the first equation from the second and simplifying a bit gives us:

$5t-5c=110$ $t-c=22$

Now, we have the following two systems, which we can add to eliminate the variable $c$ and solve for $t$ :

$\begin{cases} 4t+c=243 \\ t-c=22 \end{cases}$ $5t=265$ $t=53$

Substituting this value in the difference equation yields $c$ :

$t-c=22$ $c=t-22$ $c=(53)-22$ $c=31$

Thus, the table costs $\$53$ and the chair costs $\$31$ ; together, they cost a total of $\boxed{\$84}$ .

I think I did it the hard way.

In the following equations, the variables $t$ and $c$ represent the numbers of tables and chairs respectively

1. Write out the equations

   • Equation $(1)$ $\Longrightarrow$ $3t + 7c = 376$

   • Equation $(2)$ $\Longrightarrow$ $8t + 2c = 486$

2. Multiply both equations by 8

   • Equation $(3)$ $\Longrightarrow$ $24t + 56c = 3008$

   • Equation $(4)$ $\Longrightarrow$ $24t + 6c = 1458$

3. Subtract $(4)$ from $(3)$

   • This leaves you with $50c = 1550$ and from that, $c = 31$

4. Substitute and Solve

   • Substitute $c = 31$ in $(2)$ which gives $8t + 2(31) = 486$
   • Simplifying, you arrive at $8t = 424$ and then $t = 53$
   • Finally, you add 31 and 53 together and arrive at the answer of $\boxed{84}$