Mathathon 2021 - Sample Problem
Happy π day everyone! This is a sample problem for the Mathathon 2021 contest! Please do not post a solution if you are not a participant. Non-participants can post solutions once the contest ends, i.e April 2nd.
A circle is inscribed inside a square. If a point inside the square is selected at random, what is the probability that the point will also be inside the circle?
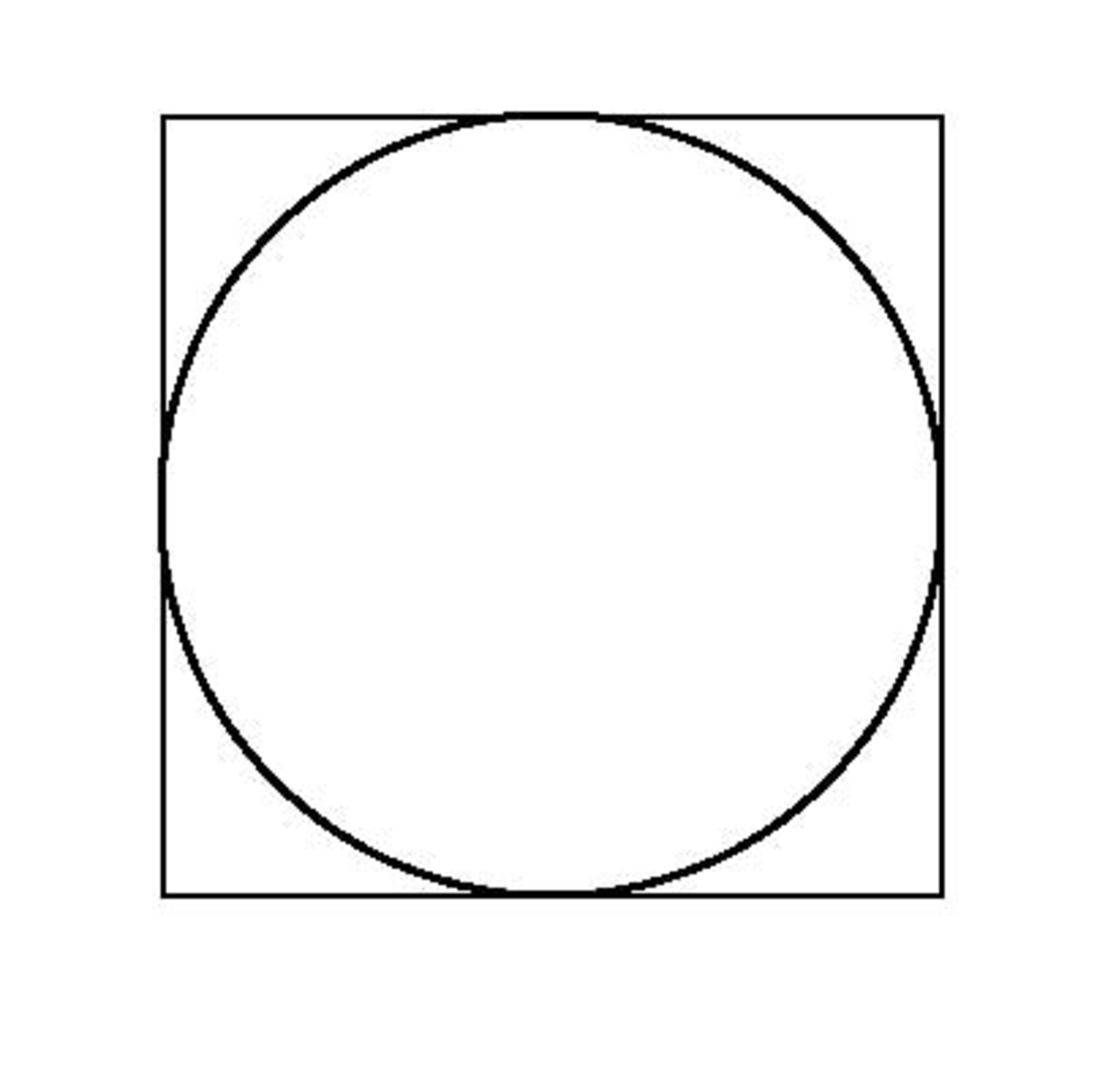 Circle inscribed inside a square
Circle inscribed inside a square
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
@Jason Gomez - I may need help understanding what's written here...😕
Log in to reply
If you randomly chose r and θ instead of x and y, points which are more far from the origin are less likely to occur compared to points closer to the origin
In short, he has proven why the point distribution shouldn’t be biased in a way(only shown one case), if it isn’t biased we get the usual 4 π , if not we can get all sort of other answers
Log in to reply
Thanks for the feedback and the summary! Sorry that my solution is so hard to read... it's difficult for me not to express myself pedantically :) But anyway, I was wondering what it means when you say that polar coordinates are biased, because I think of them as just another way of identifying every point in space and that they would be biased if they depended on some hidden parameter(s) that put some constraint on the values the coordinates can possibly take. In this case though, any point in the square can be equally described by a pair (x,y) and (r, theta). Or do you mean that, because x and y are functions of r and theta when converting back to Cartesian and now they depend on those two parameters, they are biased? Because in this case I would have to ask what makes x and y the "default", perfect, unbiased parameters. Couldn't I do it the other way around, first taking the polar probability as my base line and then randomly generate x and y values, convert them to r, theta pairs and get 4 π as my biased probability?
Log in to reply
@Oskar Dobroczek
–
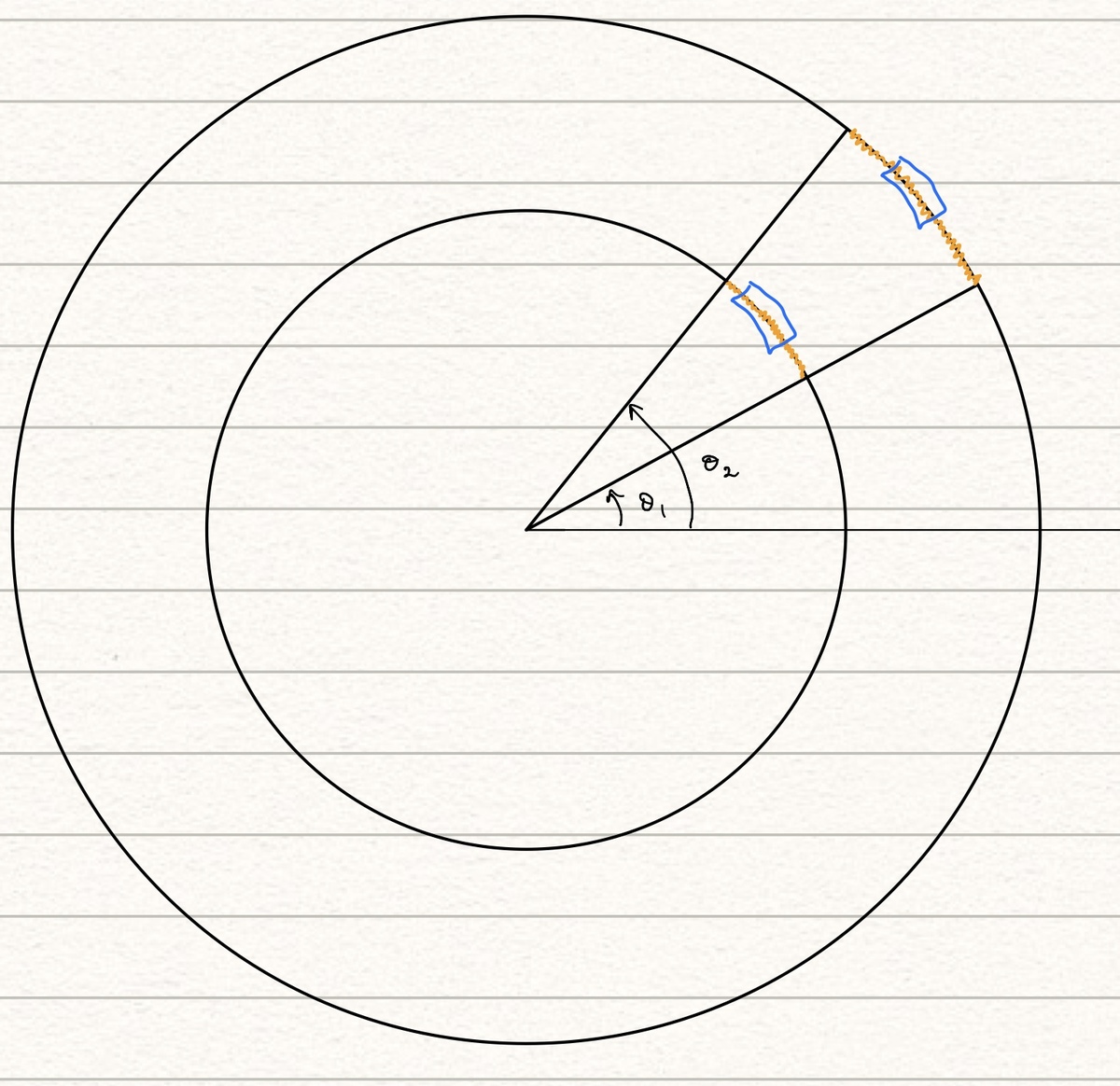 This should explain all
This should explain all
A simple translation of system or rotation shouldn’t affect the probabilities, is a general assumption/axiom {can be proved mostly but it is by itself obvious}
The rotation factor is fine with polar co-ordinaries, but not translations
The blue region in the smaller circle is more probable to have a randomly chosen point in it than the blue region in the larger circle (both are zero I agree but you know probability density functions so you should understand this statement)
Log in to reply
@Jason Gomez – aight, got it! thx for drawing the picture!
@Oskar Dobroczek - Assuming everything is correct, I'd give a 5 for accuracy, 1 for readability and 5 for ingenuity. The solution is unique for sure, but it is very long and a too complicated for a simple question. I'll have to check if everything is correct and then I'll give your scores :)
Log in to reply
The readability is actually quite good, ingenuity I don’t think it should be that high, he has just used a little more math than usual to prove both cases(showing the first case increases the readability of the solution), in a way its as simple it can be, further simplifications can’t be made easily
Log in to reply
Ok, I'm dumb...5, 3, 3 would be accurate from what you describe...
Nah you are not, it’s just something you haven’t studied (neither have I but I have an idea of how probability density functions work) yeah 5,3,3 should be accurate,
| Accuracy | 5/5 | Answer and assumptions and calculations are correct |
| Readability | 3/5 | A little too much of complications added for an easy problem |
| Ingenuity | 3/5 | Showed why Cartesian co-ordinate system is better than polar co-ordinate system for solving this problem |
| Total | 11/15 | Good job! |
| Accuracy | 5/5 | Answer and assumptions and calculations are correct |
| Readability | 3/5 | A little too much of complications added for an easy problem |
| Ingenuity | 3/5 | Showed why Cartesian co-ordinate system is better than polar co-ordinate system for solving this problem |
| Total | 11/15 | Good job! |
Let the length of the square's segments be a. The required probability that a randomly selected point inside the square will also fall within the circle = (Area of circle / Area of Square ) . Now , radius of circle = a/2. Therefore Area of circle = pi*(r^2) = pi * (a / 2) 2 = pi * a^2 / 4 . Area of square = a^2 . Therefore, the required probability = (pi * a^2 / 4) / a^2 = pi / 4
Collection of points that lie inside a polygon = Surface area of the polygon
Points inside the circle = π r 2 , where r is the radius of the circle, note that r is half the length of the side of the square which inscribes the circle (use the fact that all four of its sides are tangent to the circle). Thus the side of the square is 2 r , which gives the area to be ( 2 r ) 2 = 4 r 2 .
Note that every point that lies inside the circle will by itself be also lying inside the square, for every point inside the circle , but the converse is not necessarily true, there's a collection of points outside the circle, which is still inside the square, but not inside the circle, that make up an area of 4 r 2 − π r 2 , which should make sense as 4 > π .
In conclusion, we can say that the points inside the square make up the set of all sample points that lie inside the square and sometimes might also lie inside the circle, or the set of Cartesian points inside the square, S is the superset of the set of all points inside the circle, C , and since we're projecting all our random choices from S , S is also the Universal set here, so while calculating the possibility of a sample point being in C , we will calculate it out of the total given sample points, S . Thus,
P ( C ) = Number of sample points in S Number of sample points in C = Composition of sample points in S Composition of sample points in C = Area of the square Area of the Circle = 4 r 2 π r 2
= 4 π
A probability definition is the likelihood of an event compared to total possible outcomes. The "total" possible outcomes here is represented by the area of the square. We are interested in the likelihood of the random point to be inside the circle, hence the area of the circle.

I was minded to do some animation, so bear with it and endure lol
| Accuracy | 5/5 | Answer and assumptions are accurate |
| Readability | 5/5 | Well structured and written answer, the animation in unnecessary tho |
| Ingenuity | 0/5 | Common approach |
| Total | 10/15 | Great job! Try to limit animations to the problems where it is actually needed :) |
Don't worry about Ingenuity, as far as I know, this problem has very less room for creativity, but I promise the other problems will have multiple paths to the answer @Julie Love-Brilliant :)
| Accuracy | 5/5 | Answer and assumptions are accurate |
| Readability | 5/5 | Well structured answer, nicely spaced out |
| Ingenuity | 0/5 | Common approach |
| Total | 10/15 | Great job! No need to limit those animations, just try to make them relatable(as a random person I can’t understand what the heck is the animation for, as Jason I can tho) |
@NSCS 747 - The devil has arrived...
@SRIJAN Singh - Please don't post solutions unless you are a Mathathon member or are waiting to join Mathathon. Delete this solution. Don't reply to this comment.
Log in to reply
i wish there was a petition to ban someone ooption
Log in to reply
Yeah...or an option to block users from your notes and problems.
Log in to reply
@A Former Brilliant Member – blacklist where they can coment but cant ping or sned solution
Firstly, we define that (π(x/2)^2)/x^2)=(πx/2)^2)/x^2=(πx)^2)/4)/x^2. We can cancel both 2 and x to get π/4.
First we defined that the probability to be inside a square is: A. Circle / A. Square. A. Circle = πR^2 and A. Square = 4R^2, -> πR^2/4R^2 -> π/4 (also, R is the radio of the circle of 1: π(1*1) and in the square case we can represent as 4 = 2*2 with 1 unit R)
If you find the problem that your asterisks are creating italics rather than showing itself then do this
Replace all * with \*, it’s that simple!
I’ll grade your solution after the correction
@Jason Gomez - Elijah's not a participant. You don't have to grade non-participant solutions.
Log in to reply
Oh really lol
How can I participate?
Log in to reply
The mathathon is full, so you can't. If you wish to, you can post a comment saying you want to join in my note called 'Mathathon 2021' and if a member leaves the contest I'll add you :)
Any point in the square is equally likely. Some of those points are in the inscribed circle. The probability of a point being in a region is proportional to the area of that region. Therefore he desired probability is equal to the ratio of the area of the circle to the area of the square. Assume R is the radius of the circle. The areas are π R 2 and ( 2 R ) 2 Therefore the ratio is π / 4
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 5/5 | Well structured and written answer |
| Ingenuity | 0/5 | Common approach |
| Total | 10/15 | Great job! |
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 5/5 | Well structured and written answer |
| Ingenuity | 0/5 | Common approach |
| Total | 10/15 | Great job! (I have nothing else to say) |
Log in to reply
You literally just copy/pasted my scores and added a (I have nothing to say) lmao ...its true tho I have nothing to say either
Log in to reply
You literally just copy/pasted my scores and deleted the “I have nothing to say” lmao ...its true tho I have nothing to say either
Log in to reply
@Jason Gomez – ...I have the time advantage. My comment was posted 23 hours ago, yours only 22. So admit that you are the one who copied, or admit that I am a god with future-seeing powers :P
Log in to reply
@A Former Brilliant Member – You do know editing is a thing right
Log in to reply
@Jason Gomez – Editing? Is that some new thing you Indian's invented? Hmm...I wouldn't know...your shady president doesn't share the details with us, only conspires with China...
Log in to reply
@A Former Brilliant Member – I am not sure how the president reference works, he has been no where near the limelight since the time he was elected(maybe you meant prime minister? because he is like the president of USA), as with the conspiring with China, that too made no sense
Log in to reply
@Jason Gomez – Yes, it was not supposed to make sense...it was a joke.
Log in to reply
@A Former Brilliant Member – Ok got the context you meant, I meant you edited your grading to make it look like mine
Suppose that the circle has radius r , and the square has side length 2 r . The area of the circle will be π r 2 , and the area of the square will be 4 r 2 . Since the point has an equal probability of landing anywhere in the square, the probability that it is also in the circle is the area of the square the area of the circle which is 4 r 2 π r 2 . The r 2 's cancel, and we are left with 4 π .
was I right
Log in to reply
@Kevin Long - You should probably remove your predictions as it is unnecessary :)
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Steps to the answer flow like honey :) |
| Ingenuity | 0/5 | Your suspicions were right(I do like how you mentioned the point landing anywhere was of equal probability though) |
| Total | 10/15 | You are already ready for Mathathon :) |
Log in to reply
this was my first time using latex definitely a good learning experience
and also
ayyy i can predict the future
@Jason Gomez - Honey doesn't flow much...its very sticky. Flow like water makes much more sense...
Log in to reply
It flows smoothly unlike water, nice and slowly(I had put water first but honey was better a better description)
Log in to reply
@Jason Gomez – Water is smoother than honey...but yeah, whatever...
Log in to reply
@A Former Brilliant Member – wait i thought writing was my worst subject
guess i've been reading too many math textbooks i guess
Log in to reply
@Kevin Long – Writing isn't a subject, its torture...
Log in to reply
@A Former Brilliant Member – welp yeah pretty much
| Accuracy | 5/5 | Answer and assumptions are accurate |
| Readability | 5/5 | Answer is pleasant to read and has a proper structure |
| Ingenuity | 0/5 | The common approach |
| Total | 10/15 | Great job! |
Let the S q u a r e be the universal set.
- Now let P(C) be the probability of the point lying inside the C i r c l e
- Also let P(NC) be the probability of of the point lying outside the C i r c l e
Now we know that P(C) + P(NC) = 1 since they are complementary and we require P(C) = 1 - P(NC).
- Let the side length of the S q u a r e be 2 units
-
Now the radius of the C i r c l e = 1 unit
-
Therefore Area of the S q u a r e = 2 ∗ 2 = 4
- And the Area of the C i r c l e = π ( 1 ∗ 1 ) = π
- P(NC) = 4 4 − π = 1 - 4 π
Therefore our required answer P(C) = 1 - P(NC) = 4 π
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 3/5 | Increased complexity of solution by finding P(NC) to find answer (should have been done as a side note instead) |
| Ingenuity | 2/5 | Use of set theory |
| Total | 10/15 | The simpler the solution the more readability points :) (Anything more which can be added should be done separately after the answer is found) |
Log in to reply
I kind of went the round about way , so that it won't be same as the common solution
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 3/5 | Set theory could have been explained a bit better, or introduced in a side note |
| Ingenuity | 3/5 | Set theory and probability has been well used |
| Total | 11/15 | Great job! |
We have to calculate the probability that a random point selected in the interior of the square is also inside the circle.
Let r be the radius of the inscribed circle. If we increase r to kr (k is constant) the area of the circle as well as the square will increase by the same proportion that is k^2.
From this it is clear that for any value of 'r' the probability will be the same.
So lets take r=1
- area of circle = πr^2 = π* 1 *1 = π
- area of square = side^2 = (2r)^2 = (2*1)^2 = 4
Therefore, the probability of required event = 4 π
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Very nicely structured answer |
| Ingenuity | 2/5 | Reduced the problem to a single case |
| Total | 12/15 | Perfect format of an answer, ingenuity points are normally hard to get, so no one gets a full here (it’s possible for harder problems) , near to ideal solution :) |
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 5/5 | Everything is clear and well structured |
| Ingenuity | 2/5 | Showed that it is possible to use a single case without l.o.g |
| Total | 12/15 | Great job! Your total score is currently the highest! |
Let a be the side of the square
Then the area of square would be a 2 And since the diameter of the circle = the side of the square=a the radius of the circle,which is half times diameter will be 2 a Now we can substitute the value of r in π ∗ r 2 (which gives us the area of a circle)
4 π ∗ a 2
Now, the probability of a point lying in the square:
p(s)=1(because there can't be any point outside it ,assuming that it was our universal set)
The probability of a point lying in both square and circle
p(s∆c)=p(c)(because c is a subset of s)
And clearly,
p(c)= a 2 π ∗ a 2 =π/4
Hence option b is correct!
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 4/5 | Proper steps have been used but proper parentheses not used |
| Ingenuity | 1/5 | A little set theory is used |
| Total | 10/15 | Great job! Your readability can be a bit better :) |
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 4/5 | π*a^2/4 could have been written as (π*a^2)/4 which doesn’t make the 4 look like the denominator of 2 |
| Ingenuity | 2/5 | A touch of set theory nicely done |
| Total | 11/15 | Congrats, a little more tour on latex could help you on ensuring those readability points |
Log in to reply
Try replacing π*a^2/4 with \ (\frac{πa^2}4\)
Exotic explanation looking for ingenuity points :
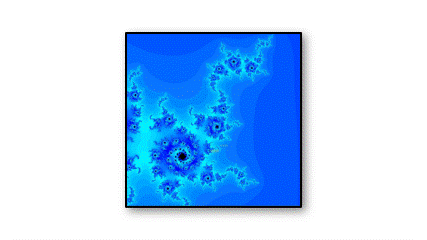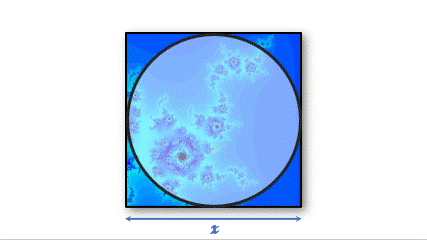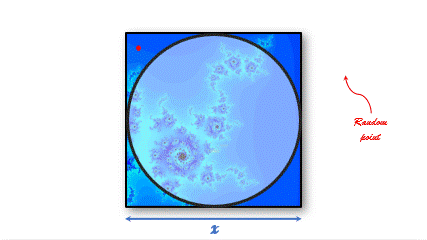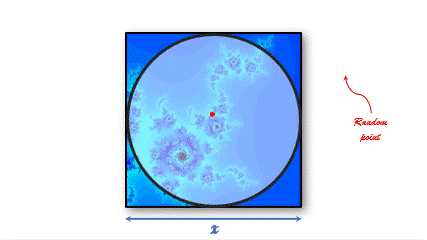
I took a a quadrant inscribed in a unit square.
I uniformly (randomly) scattered a given number of points over the square.
I counted the number of points inside the quadrant.
Then I evaluated the ratio :
p
i
/
4
.
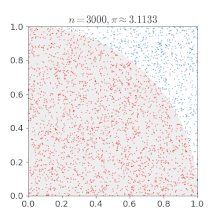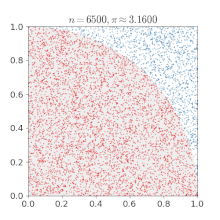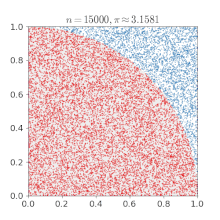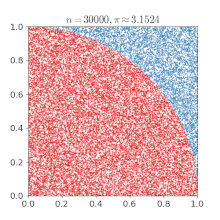
Not the quickiest way but it works !
The same approach has been used to evaluate p i and is known as the Monte Carlo method.
Would you like your scores @Guillaume MARTIN ?
Yes please !
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 3/5 | Answer is simple and readable, but time-taking way to solve the problem. Good use of image :) |
| Ingenuity | 1/5 | A different method, albeit less efficient |
| Total | 9/15 | Ingenuity points come from clever solutions, not just different, try to improve that :) |
I tried to find a clever solution but the problem is very close to p i definition (if not confused with), leaving I think no space for other smart ways.
By the way I had a lot of fun imagining this solution :)
| Accuracy | 4/5 | Has not been mentioned that probability will tend to 4 π |
| Readability | 4/5 | Simple answer nicely presented, can increase the size of the gif so numbers are visible |
| Ingenuity | 1/5 | Different method, but not a very feasible method |
| Total | 9/15 | Higher ingenuity points comes with solutions that are human possible, but still can’t be made by many |
You're right for :
1. Accuracy : I should have explain that this ratio converges.
2. Readability: I did increase the size of gif file.
3. Ingenuity: this solution gives you a true value which, in the mainstream solution, is very hard to obtain without knowing the value of
π
.
Anyway this sample problem shows the spirit of this contest and hence is very usefull.
Thanks to you and @Percy Jackson
Log in to reply
You are welcome :), please do not edit (grammatical corrections are fine) the solution after we have graded for the real Mathathon Problems, unless you haven’t completed the solution which can be avoided by including “Explanation/Solution under construction”
Log in to reply
Well received.
I didn't correct my solution (introducing convergence...) , just increased the size of the gif file.
Regards
Probability = what you could get what you want to get . In this case, it is the ratio of S ∘ to S □ which is just 4 π .
@Jeff Giff - Shall I score your solution, or are you still working on it?
| Accuracy | 5/5 | Answer and assumptions is accurate |
| Readability | 3/5 | Proper steps have not been used. Answer has been given directly. |
| Ingenuity | 0/5 | Answer is same as common answer |
| Total | 8/15 | A bit more structured calculation can get you that 15! |
| Accuracy | 5/5 | Answer and principle used are correct |
| Readability | 2/5 | Could have mentioned what S stands for (not common notation for area or set) |
| Ingenuity | 2/5 | Solved with the help of a set(I assume) |
| Total | 9/15 | Explanation of un-common terminology would have got you a 12! |
Log in to reply
I won’t change my grading but please do tell me what you meant by S, was it set or area
Most Common Solution -
The probability that a point in the square is also a point in the circle is nothing but the ratio of the circle's area to the square's area.
Let the radius of the circle be r . Then the side of the square is of length 2 r . Then, the areas of the circle and square are π r 2 and 4 r 2 respectively.
Thus, the answer is 4 r 2 π r 2 = π / 4
If your answer follows the exact same method as this, Ingenuity points will not be awarded.
I will give scores out of 15 and so will Jason. Combining our scores will give you a score out of 30 :)
@Percy Jackson , please don't give a problem like this , or I will again get 100 points LOL
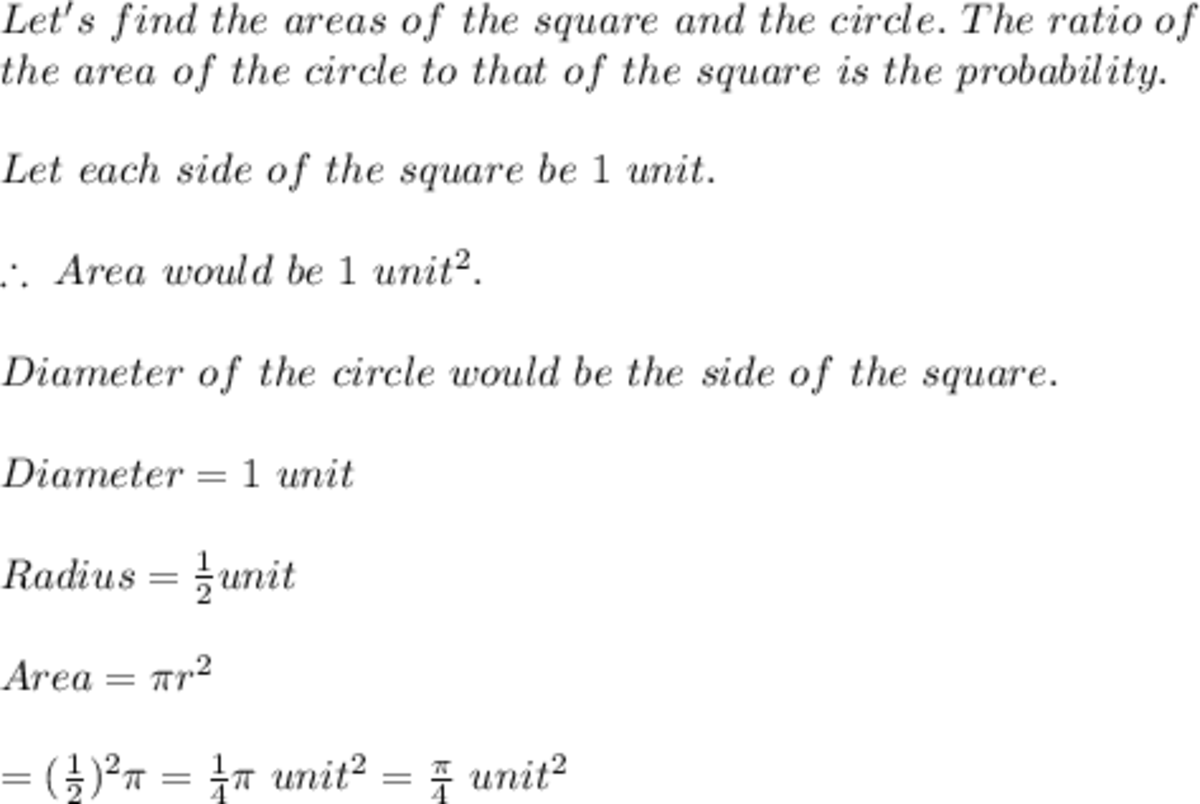
Okay, so to get the most obvious answer out of the way, let l be the diameter of the circle. It follows that the circle has area A ∘ = π l 2 and the square has area A □ = ( 2 l ) 2 = 4 l 2 .
Intuitively, we can say that the area of the square encompasses all possible points, whereas the area of the circle is comprised of only the points that we 'want'. Thus, it makes sense to take the ratio of the two and interpret it as the probability that a randomly chosen point lies inside the circle. Let this probability be p cartesian . It's easy to see that p cartesian = A □ A ∘ = 4 l 2 π l 2 = 4 π . NOW, what's always important with probability is to explain your method of selecting values. I will show why this matters. You can, for example, compare the probabilities when using Cartesian and polar coordinates using code and see that you get different results with the probability in polar coordinates p polar ≈ 9 0 % .
When thinking more deeply about the problem, the fact that the probability is related to the areas of the circle and square required some explanation to me. Since the probability does not in any way seem to be proportional to the radius/side length of either the circle or the square, I will simplify the following calculations by letting the square be have side length 2 and the circle be a unit circle. If we say that we place the two in a Cartesian coordinate system, both centred at the origin, we get the following description: ◯ = { ( x , y ) ∈ R 2 ∣ x 2 + y 2 ≤ 1 } , □ = { ( x , y ) ∈ R 2 ∣ ∣ x ∣ ≤ 1 and ∣ y ∣ ≤ 1 } . Probability in Cartesian coordinates:
The first method that I came up with to randomly choose a point goes as follows:
Randomly choose a value x p ∈ R , ∣ x p ∣ ≤ 1 . All x -values inside the interval have the same probability of being chosen.
Now choose a value y p ∈ R , ∣ y p ∣ ≤ 1 . All y -values inside the interval have the same probability of being chosen.
If x p 2 + y p 2 ≤ 1 , the point p = ( x p , y p ) is considered inside the circle. If x p 2 + y p 2 > 1 , the point is outside the circle.
To yield the same probability without initially resorting to areas, I will use probability density functions. This class of functions has, among others, the following properties:
The integral between two points of its domain represents the probability that an object is within the interval between the two points.
The integral over its entire domain is normalised to equal 1. This makes sense since the object has to be somewhere.
I use this kind of function because for a point in the reals, the actual probability for that point to be selected is 0 because there are infinitely many points around it that could also be selected.
Now comes the juicy part! To calculate the total probability I will make use of the fact that the first two steps of the algorithm above can be assigned a probability density function. Multiplying these functions is like multiplying discrete probabilities, only that we have to integrate over the desired domain (the circle) to get a real probability.
So let Ψ x be a probability density function on R with domain
{ x ∈ R ∣ − 1 ≤ x ≤ 1 } . and Ψ y be a probability density function also on R with domain: { y ∈ R ∣ 0 ≤ y ≤ 1 } . Note that I only include half of the square, which, as a quick calculation using the area method shows, should not change p cartesian . The same probability p cartesian will be calculated as p cartesian = ∬ 2 1 ∘ Ψ x ⋅ Ψ y d x d y , where Ψ x , Ψ y are the probability densities that a random point gets picked.
To determine Ψ x and Ψ y , note that they have to be constant since the probability is constant. This will be useful when normalising: ∫ − 1 1 Ψ x d x Ψ x ∫ − 1 1 d x = 2 Ψ x ⟹ Ψ x ∫ 0 1 Ψ y d y Ψ y ∫ 0 1 d y = Ψ y ⟹ Ψ y = ! 1 = 2 1 = ! 1 = 1 Parametrizing the circle leaves the following integral to be evaluated: p cartesian = ∫ x = − 1 x = 1 ∫ y = 0 y = 1 − x 2 Ψ x ⋅ Ψ y d x d y . And this is where the area comes into play. Because both probabilities are constant, we only have an integral over the semicircle left to be evaluated. This corresponds to its area. ∫ x = − 1 x = 1 ∫ y = 0 y = 1 − x 2 Ψ x ⋅ Ψ y d x d y let x d x ⟹ p cartesian p cartesian = 2 1 ∫ x = − 1 x = 1 1 − x 2 d x = cos ( ϕ ) , ϕ ∈ [ 0 , π ] = − sin ( ϕ ) d ϕ = − 2 1 ∫ ϕ = π ϕ = 0 1 − cos 2 ( ϕ ) sin [ ] ( ϕ ) d ϕ = 2 1 ∫ ϕ = 0 ϕ = π sin 2 ( ϕ ) d ϕ = 2 1 ⋅ 2 π = 4 π and, oh wonder I get the same answer!
But this is where the story gets interesting, because I now took a look at polar coordinates.
Probability in polar coordinates
To explain the higher probability when using polar coordinates, I constructed a similar algorithm for choosing a random point. Only note that the maximum length of r is now a function of ϑ , which i will evaluate only in the first eighth of the circle. To see why this function is r = sec ( ϑ ) , you can draw the square and see that cos ( ϑ ) = r 1 for ϑ ∈ [ 0 , 4 π ] because the square's side for positive x -values stays fixed at 1. This saves some computation effort and seems reasonable, as all other parts of the circle are symmetrical to its first eighth and the area method gives the same probability for this section of the circle as for the whole thing. So here's the algorithm:
Randomly choose a value ϑ p ∈ R , 0 ≤ ϑ p ≤ 4 π . All ϑ -values inside the interval have the same probability of being chosen.
Now choose a value r p ∈ R , 0 ≤ r p ≤ sec ( ϑ p ) independently of your choice for ϑ p . All \r -values inside the interval have the same probability of being chosen.
If r p ≤ 1 , the point p = ( r p , ϑ p ) is considered inside the circle. If r p > 1 , the point is outside the circle.
Once again, for computing the probability p polar , I will resort to probability density functions which will give the following integral to evaluate: p polar = ∬ 8 1 ∘ Ψ θ ⋅ Ψ r d r d ϑ .
Determining Ψ ϑ goes as follows: ∫ ϑ = 0 ϑ = 4 π Ψ ϑ d ϑ Ψ ϑ ∫ ϑ = 0 ϑ = 4 π d ϑ = 4 π Ψ ϑ ⟹ Ψ ϑ = ! 1 = 1 = π 4 and although r is now a function of ϑ , Ψ r still has to be constant for any ϑ because every value of r has the same probability of being chosen on the length which is determined by ϑ . ∫ r = 0 r = sec ( ϑ ) Ψ r d r Ψ r ∫ r = 0 r = sec ( ϑ ) d r = cos ( ϑ ) Ψ r ⟹ Ψ r = ! 1 = 1 = cos ( ϑ ) Plugging this into the integral, we get p polar p polar = π 4 ∫ ϑ = 0 ϑ = 4 π ∫ r = 0 r = 1 cos ( ϑ ) d r d ϑ = π 4 [ sin ( ϑ ) ] ϑ = 0 ϑ = 4 π = π 4 ⋅ 2 1 = π 2 2 ≈ 9 0 % which completely agrees with the observations.
Using probability density functions, I have shown that evaluating probabilities for processes like the one described in the problem depends heavily on the method of selecting values.