Max Charge Kinetic Energy

Electricity and Magnetism Level 4

There is a massive charged particle $(m = \SI{4}{\kg}, q = \SI{2}{\coulomb})$ at rest at the origin $(x = \SI{0}{\m})$ at time $t = 0$ . The particle is influenced by an electric field oriented purely in the $x$ direction. Its value is given by:

$E_x = 3e^{-t} \hspace{0.2cm} \frac{\text{V}}{\text{m}}$

As time tends toward infinity, the particle's kinetic energy converges upon what limiting value (in Joules, to 1 decimal place)?

Note: All physical quantities are in standard SI units.

The answer is 4.5.

2 solutions

Steven Chase
Oct 22, 2016

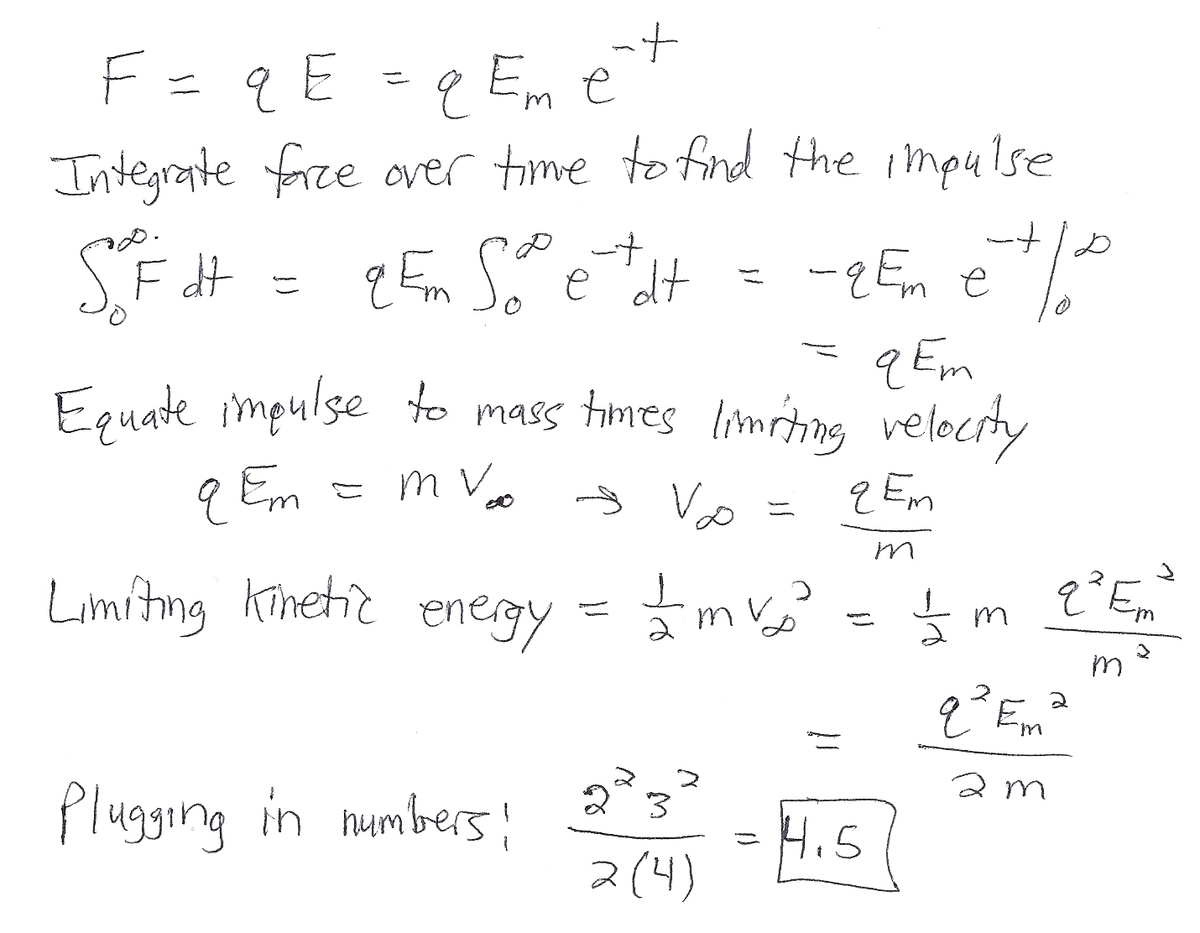
Now try making one where Ex AND Ey both are present

Md Zuhair - 3 years ago

Sounds fun. Would you like to post it?

Steven Chase - 3 years ago

Ummm... would you like to post it? I have my exams going on. So making a problem would be time taking. Would you mind posting it?

Md Zuhair - 3 years ago

@Md Zuhair – Sure, I'll post it

Steven Chase - 3 years ago

@Steven Chase – Thanks sir. Please let me know when you post it. Thanks.

Md Zuhair - 3 years ago

Aditya Narayan Sharma
Jan 25, 2017

Also, $\displaystyle m\ddot{x}=6e^{-t} \implies v_f = 6\int_0^\infty e^{-t} \; dt = 6$

So, $K=\frac{p^2}{2m}=\frac{6^2}{8}=\boxed{4.5}$

Max Charge Kinetic Energy

The answer is 4.5.

2 solutions

0 pending reports