Maximize Evaporation -- Disk Wheel Humidifier

Calculus Level 4

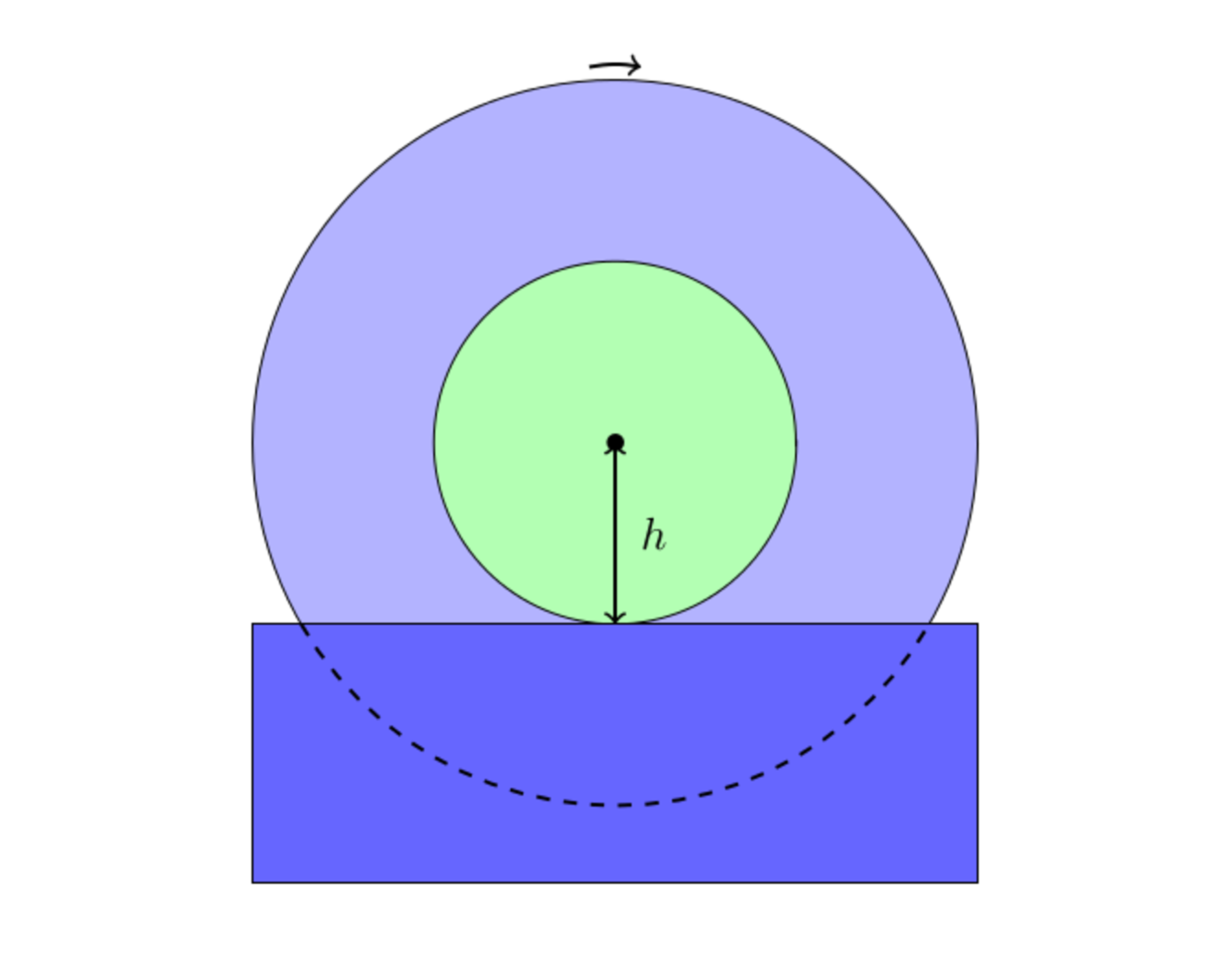
A circular disk which is perpendicular to the water surface (partially submerged) keeps rotating slowly, as shown in the figure. What should be the height of the center of the disk from the surface of water, so that the area of the wet surface above the water is maximized?

In other words, find $h$ such that the blue area above the water surface is maximized. And then, assume the radius of this disk as 3 units, and enter your answer to at least 3 decimal places.

The answer is 0.9099434.

1 solution

Gopinath No
Jul 10, 2016

Let $r$ be the radius of the disk, and $h$ be the height of the center above the surface of water.

Now, the wet surface above the water level will be --

$A = h \sqrt{r^2-h^2} + r^2 \arcsin {\left(\dfrac{h}{r}\right)}+\dfrac{\pi r^2}{2}-\pi h^2$

Solving for $\dfrac{dA}{dh} = 0$ and checking for the one giving max value, we obtain $h = \dfrac{r}{\sqrt{1+\pi^2}}$

Hence, for $r=3$ , $h\approx 0.9099434$

i could'nt understand solution plz explain why the last two terms are included ? ( expression of area)

A Former Brilliant Member - 4 years, 10 months ago

First, and second term together represents the area below the diameter but above the water level. Third term's the area above the diameter. And the last term, $\pi h^2$ is the area that doesn't get wet, so needs to be subtracted.

gopinath no - 4 years, 10 months ago

sorry to disturb you again but i did'nt understand why pi h^2 area did'nt get wet ?

A Former Brilliant Member - 4 years, 10 months ago

@A Former Brilliant Member – $h$ is the height above water. We can see that when it rotates, that circular area won't touch the water..

gopinath no - 4 years, 10 months ago

Maximize Evaporation -- Disk Wheel Humidifier

The answer is 0.9099434.

1 solution

0 pending reports