Maximize Volume of an Open Box
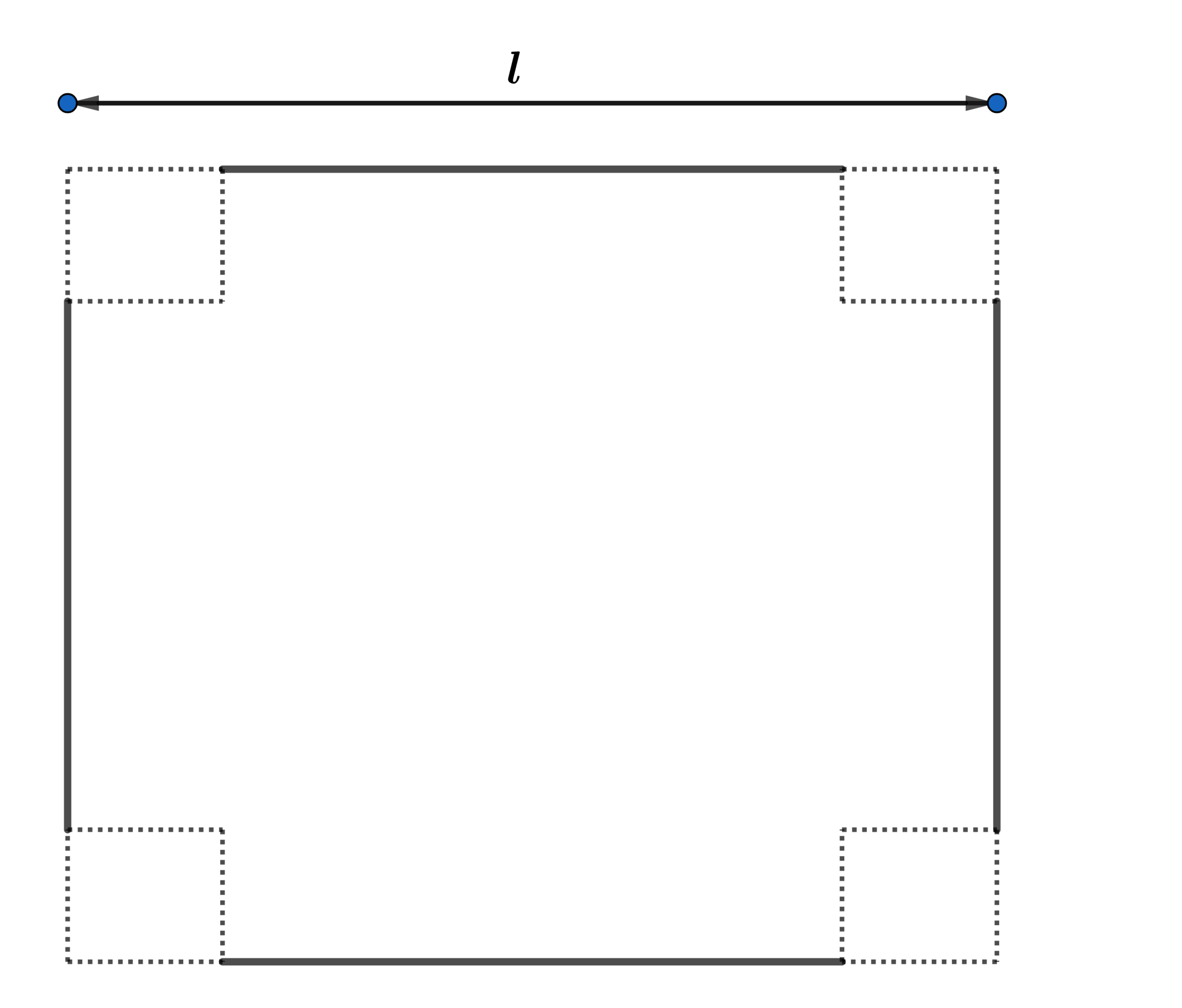
In the diagram above, a square is cut out of each corner of the above square with side length l to form an open box.
Find the value of l for which the maximum volume V of the open box is V = 2
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I think you should say something about x = l/6 being a local max as opposed to a local min.
Log in to reply
Using the second derivative test we obtain:
d x 2 d 2 V ∣ x = 6 l = ( 2 4 x − 8 l ) ∣ x = 6 l = − 4 l < 0 ⟹ local max at x = 6 l .
Log in to reply
Thank you.
Let each side of each small square be of length x . Then V = x ( l − 2 x ) 2 . Now the A.M. of l − 2 x , l − 2 x and 4 x is greater than or equal to their G.M. That is, 3 l − 2 x + l − 2 x + 4 x ≥ 3 4 x ( l − 2 x ) 2 or 4 x ( l − 2 x ) 2 ≤ ( 3 2 l ) 3 , or x ( 2 l − x ) 2 ≤ 2 7 2 l 3 . Therefore 2 7 2 l 3 = 2 or l = 3
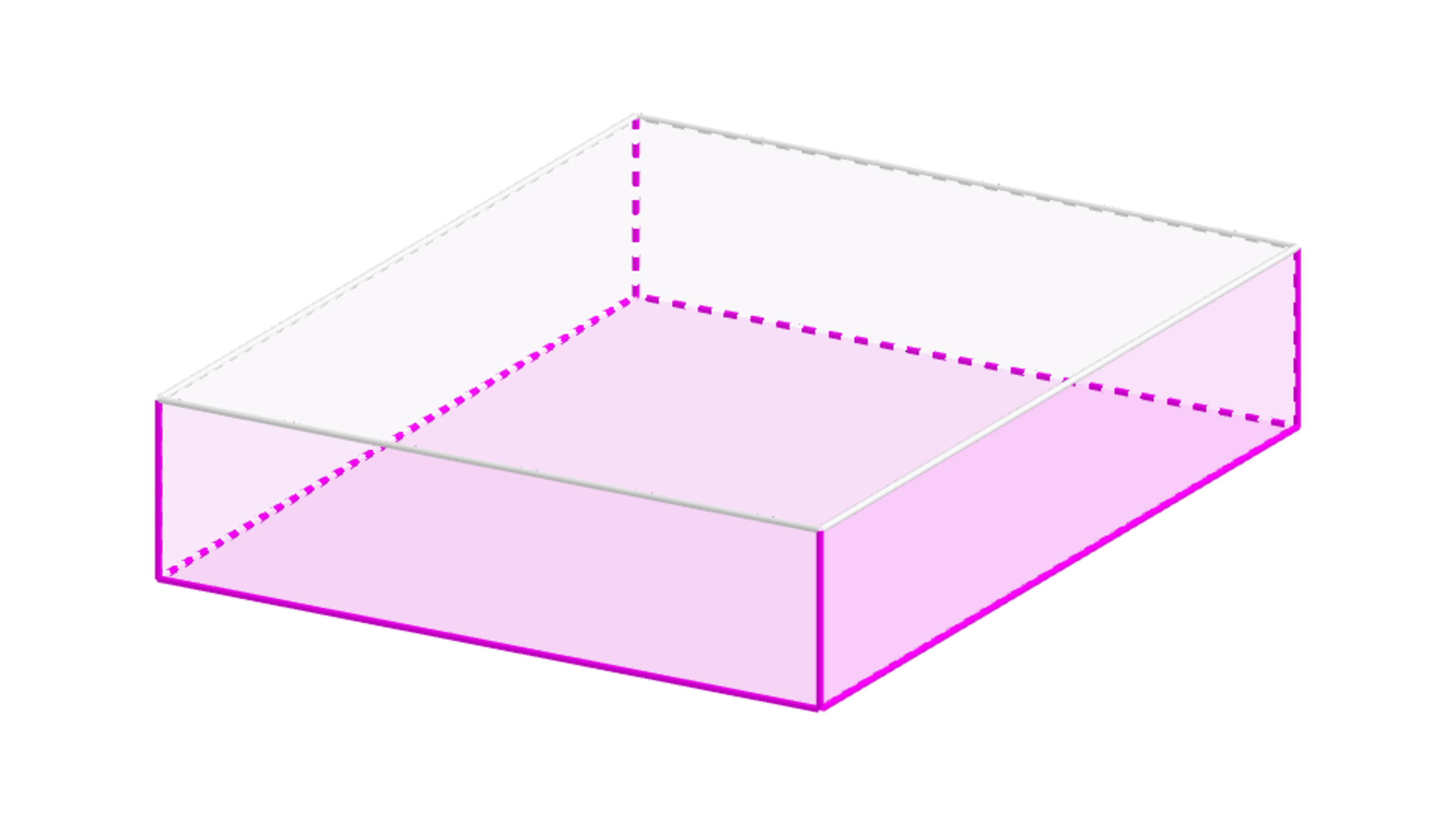
Using the above diagram the volume V = ( l − 2 x ) 2 x = 4 x 3 − 4 l x + l 2 x ⟹
d x d v = 1 2 x 2 − 8 l x + l 2 = 0 ⟹ x = 2 4 8 l ± 4 l = 2 l , 6 l
x = 2 l ⟹ V = 0 ∴ we drop x = 2 l and choose x = 6 l ⟹ V = 2 7 2 l 3 = 2
⟹ l = 3 .
Note: Using the second derivative test we obtain:
d x 2 d 2 V ∣ x = 6 l = ( 2 4 x − 8 l ) ∣ x = 6 l = − 4 l < 0 ⟹ local max at x = 6 l