Maximizing Area/Perimeter
Within a 1 0 0 × 1 0 0 square, draw in a shape that maximizes the ratio Perimeter Area .
What is this ratio (to 2 decimal places)?
For example, if we drew in a 1 0 0 × 1 0 0 square, we would get 4 × 1 0 0 1 0 0 2 = 2 5 .
The answer is 26.51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The interesting thing about using physical analogies here is that unlike soap bubbles, which seeks to minimize perimeter (or surface area) for a given area (or given volume), we're seeking to minimize the ratio of area over perimeter. But, given a finite exterior boundary, what would compel the interior closed figure to seek and settle at the maximum ratio?
Log in to reply
If you imagine this band to actually be inextensible, and with perimeter p , we see that blowing more air inside it will produce a curve that maximizes area for that given perimeter (it is also the curve with smallest perimeter for that area), and since the perimeter is fixed, it will also maximize the ratio r = p A . This means there is a function r max ( p ) , that gives this maximal ratio for every p . Now, we just need to finde the maximum value of this function. In my solution, I just rewritten everything as a function of another variable, x , and did that.
There is nothing special about the band being expandable, I just put it like that because it makes it easier to imagine it continuously changing size. In fact, this rubber band with air inside doesnt seek that smaller ratio, if you put too much air the area will eventually become the entire square and the ratio will go back to 2 5 , and if you put too little, it will just be a circle with radius R and ratio R .
Log in to reply
Let's suppose there is just enough perimeter in an inextensible band to make a perfect circle that touches the side of the square. This wouldn't yield the maximum P A , since obviously you showed a solution that would. If the band is elastic, and we keep blowing air inside, then it will pass the point of maximum P A until it fills the square completely. It is curious to me that in both cases, if the side of the square or the diameter of the circle is s , then P A = 4 s , and the maximum possible is just a bit higher, 0 . 2 6 5 .
So, what physical process would result in a figure settling on this maximum? Does this have any real life application?
(Very nice setup. This was how I "intuited" the shape of the answer, but I didn't feel it was rigorously done due to the constraint of the walls.)
Note: The
r
m
a
x
(
p
)
version is much cleaner, because then we just need to find
max
p
r
m
a
x
(
p
)
.
In the case of resorting to
x
, you're making an assumption that there is a corresponding
x
value for every
p
, which is not true.
IE If you wanted to find the minimum value, then you would conclude that the min occurs when x = 0 , 5 0 , or that p A = 2 5 , when actually the infimum value is 0.
Log in to reply
@Calvin Lin – I think this is a very "intuitable" problem, and readily come to the conclusion that the ideal shape will be composed of parts of perimeter that matches the closed exterior boundary and circular arcs that are tangent to the boundary. However, the last step of the proof which is to show that replacing an circular arc that is not tangent to the exterior boundary with one that is will always improve the ratio isn't readily apparent (except intuitively), but I will try to include that in my incomplete proof.
@Calvin Lin – Yeah, this really isn't a rigorous explanation, it just gives good intuition. On the one-to-one correspondence between x and p , it is obviously not true in general, but it is if we restrict ourselves to the rubber band shapes, right? I mean, x isn't even defined for all shapes
See my revised reply
Interesting follow up question... What about maximizing the volume to surface area inside a 100x100x100 cube?
Log in to reply
I don't know if I should post the answer here, but the mathematics of this 3D version is pretty untidy, requiring solving a cubic with messy roots. Once again, both the cube and the inscribed sphere have the same ratio P A = 6 s , while the maximum possible is higher than either.
I did this but it was out of pure intuition and I don't think I should have gotten this right
Log in to reply
Dan, I'm STILL trying to prove this "rigorously"! Of course when I first solved this, I used pure unfiltered intuition, organic grade.
I think you can do a little better. Consider the intersection of the square and a circle with radius 58.348.
The ratio of the area to perimeter will be 27.61 which is slightly better (assuming my numerical optimization worked.)
The difference is that I don't force the curved bits to be 90 degree arcs (this is an inefficient restriction, I believe). However it's conceivable that I messed up.
Log in to reply
I'll check on that right now, and will get back to you.
Log in to reply
Okay, using 2 variables, x and r, where x is the distance from the corner to the beginning of the arc, and r being the radius of the arc, I've plotted out the ratios for an unit square. The maximum is 0.265, which occurs when x = r . In other words, quarter rounds at the corners.
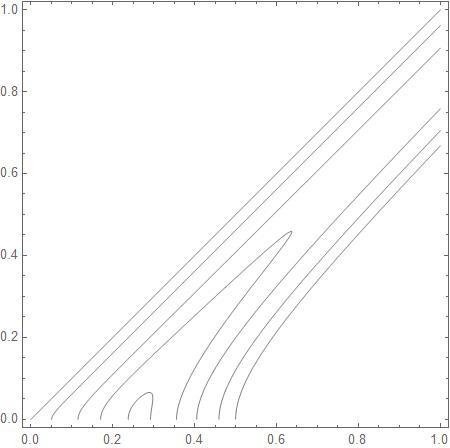
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
1 2 3 |
|
How do we know when to “stop” blowing air into the rubber band? If we were to keep going the rubber band would approach a square, and if we stop early the band becomes closer to being a circle, so what’s the reasoning for stopping at this specific point (where the end circles have the maximum radius as seen below)?
Log in to reply
That's right, when is it time to stop? See the last example I gave in my solution, where the exterior is a smaller square combined with a larger. And, worse, I can't seem to prove that all circular arcs produced in this way are necessarily tangent to the exterior boundary, even though that part seems to be true.
Log in to reply
While it definitely makes intuitive sense that the arcs would be tangent, the ideal radii for the arcs seem to be somewhat “random”. Especially if we assume that all arcs formed are tangent to the box, what makes that radius so special?
As a somewhat side note, how could the area to perimeter ratio be maximized if there was a smaller square gap in the middle of the 1 0 0 × 1 0 0 square? More specifically, how would the figure act around the inside corners? I was wondering if considering this case would provide any insight into why the specific radius maximizes the ratio.
Log in to reply
@Calvin Osborne – What would happen is that the ratio will drop, the larger the square hole inside, the lower the ratio. But the odd fact remains that the radius of the quarter circles is still the same as that ratio. For a square hole of side 2 0 , the radius and ratio works out to a particularly neat
6 + 6 ( 2 + π ) 2 4 0 = 2 0 . 7 7 1 6
When to "stop" is indicated by the x in the function. By calculus we can find the maximum value of it. (That's what I think though)
I must have made a rounding mistake, I came up with 26.50, after making a shape of four circles with radius 25 connected with line segments, I calculated Area at 9463.4954, and Perimeter at 357.0796, so A/P = 26.502. When I saw I got it wrong, I panicked and looked at the answer.
proof under construction still not complete!
The problem of "maximizing the ratio of area to perimeter" is that it is related to but not the same as the classic isoperimetric problem, which asks for the maximum possible area for a given perimeter. See 2D Isoperimetric Theorem. However, if the perimeter is not a given, and is allowed to vary without any constraints, then consider a circle of radius r , which has an area of π r 2 and perimeter of 2 π r , so that the ratio becomes 2 r , which means any ratio depending on choice of r . Then such problems require constraints on the area and perimeter in order to have unique (or finite number?) of such ratio maxima, such as having a bounding closed exterior figure, such as a square.
Let there by a closed figure with an area A and perimeter P , so that the ratio is P A . Then we can do any of the following which all will improve that ratio. When speaking about segments of the perimeter, we will only consider the length of that segment of the perimeter and do not count the distance d of that segment.
1)
We can scale up the closed figure by any factor
s
, so that this ratio is increased by that factor
s
2)
Let there be a segment of its perimeter which has length
q
, and such that its end points are separated by some straight distance
d
<
q
and the segment does not cross the line
d
. Then if we are able to increase the area
A
by
b
by changing that segment of the perimeter while reducing its length to distance
d
by making it a straight segment, we have a new ratio
P
−
(
q
−
d
)
A
+
b
, which is greater than what it was before. Thus, any closed figure made convex by this means will have an improved
P
A
ratio.

3)
Let there be a segment of its perimeter which has length
q
, its end points separated by some distance
d
. Then if we are able to increase the area
A
by
b
by changing that segment of the perimeter without changing its length
q
or distance
d
, we have a new ratio
P
A
+
b
, which is greater than what it was before. The maximum that this ratio can be improved is if this segment takes the shape of an arc of a circle. Or a whole circle if we maximize the area
A
for its given perimeter
P
.
4)
Let there be a segment of its perimeter which has length
q
, its end points separated by some distance
d
. Then if we are able to reduce the perimeter
P
by
c
by changing that segment of the perimeter without changing the area
A
or distance
d
, we have a new ratio
P
−
c
A
, which is greater than what it was before. The maximum that this ratio can be improved is if this segment takes the shape of an arc of a circle. Or a whole circle if we minimize the perimeter
P
for a given area
A
.
5)
Now, we look at where an arbitrary segment of the perimeter is bounded by two straight sections . There exists a circular arc that is tangent to both straight sections that while the area is unchanged, the perimeter can be reduced. This new circular arc intersects the old perimeter such that the net of bounded areas can be made
0
(Intermediate Value Theorem), and the perimeter is shortest (per Isoperimetric Theorem). This is not the same as
4)
because the size and location of the circular arc tangent to the straight segments determines where line
d
goes. For this reason, applying this step may not always be possible.
By applying 2), 3), 4) repeatedly, we can arrive at a convex figure which perimeter is composed of straight segments and circular arcs, which we'll call a straight+arc figure. And by applying 5) , we can arrive at a figure where the circular segments are tangent to the adjoining straight segments, but not always, if boundary conditions prevent this step.
If the closed figure has to be contained within a square, then provided if it's ultimately convered into a straight+arc figure without touching the sides, the new figure will have increased P A ratio, which we can then rotate and scale up until it touches the square at all four sides (using the Intermediate Value Theorem). If the closed figure is already or ends up touching at least 2 opposite sides of the square, then we can expand it until it touches the square on all four sides by adding a parallelogram section of area s x , where s is the length of the side of the square, and x is the distance the sections to be separated by this addition. Hence we've improved the ratio further
P A < P + 2 x A + s x
which follows from the fact that
P A ≤ 2 s
since any closed figure with a "width" of
s
cannot have a ratio
P
A
that exceeds this. An rectangle of one finite width
s
and one infinite length has ratio
2
(
s
+
L
)
s
L
=
2
s
as
L
→
∞
.
A circle has the same property.
So, finally, from this and by use of
2), 3), 4), 5)
, we can have a figure inscribed inside the square which are characterized by quarter circles at the corners (or with some circular arcs which terminates at the vertices--see below). We can draw smaller squares at each corner, so that if the ratio
P
A
(counting only perimeter length from side to side and not counting any other perimeter to make it closed) is greater for any one of them as compared to another square of the same size, then we can replace the one with the smaller ratio with the larger. If all the quarter circles have a radius equal to or less than half of the side length of the square, then they can immediately be made all alike, so that the figure is symmetric with respect to both axes. Otherwise, we have a figure with two pairs of different quarter circle radii.
Let r 1 , r 2 be the two possible radii, in a square of side length s . Then the area and perimeter are as follows
A
=
2
1
π
(
r
1
2
+
r
2
2
)
+
s
2
−
2
(
r
1
2
+
r
2
2
)
P
=
π
(
r
1
+
r
2
)
+
4
s
−
4
(
r
1
+
r
2
)
Optimizing the ratio P A gets us
r 1 = r 2 = 2 + π s , so that for s = 1 0 0 , the maximum ratio is 2 6 . 5 0 7 9 . . .
In one special case of two quarter arcs meeting at corners (which has the maximum ratio
P
A
of all variations of circular arcs meeting at the corners) so that none of the steps
1), 2), 3), 4), 5)
can readily be used to improve on the ratio
P
A
(we can use
4)
converting the interior figure into a circle with same area, but this require computational work to ensure it fits within the square), we can still go ahead with the method used to determine
r
1
,
r
2
by starting with
r
1
=
0
.
There are still other special cases where circular arcs end at vertices and are not necessarily tangent to both sides, such as
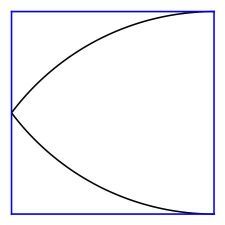
of which this one can be improved by application of 5) by replacing the two circular arcs with a semicircle tangent to the sides other than at the vertices, and then expanding until the figure once again meets all four sides of the square. Then we end up with the general case of corners truncated by quarter circles of two different radii.
In the general case of finding the maximum ratio P A of any interior closed figure bounded by a closed exterior figure, the optimum interior figure will always have its perimeter coinciding with that of the exterior figure and/or having circular arcs that are tangent to the exterior figure. Then, for a given closed exterior figure, all such tangent circular arcs will have to be balanced for maximum P A , as most of the time using 1), 2), 3), 4), 5) alone wil not be able to make this determination. For example, one could start out with an interior closed figure that has a longer perimeter than the perimeter of the exterior figure bounding it. Then by using 3) , we can expand the interior closed figure to match the exterior closed figure, which may not yield maximum P A , even though it is greater than what it was before.
Addendum:
Here's a difficulty with assuming that expanding any circular arc into one that is tangent to the sides of the exterior boundary, while not changing where it touches it, will always improve the ratio
P
A
. It doesn't always work. Have a look at this figure. The perimeter of the interior figure includes the blue circular arc
b
and the sides of the large square, but without the quarter round cyan
c
cutouts.
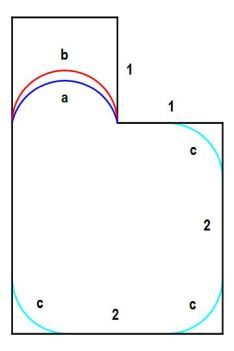
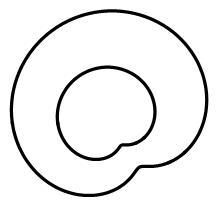
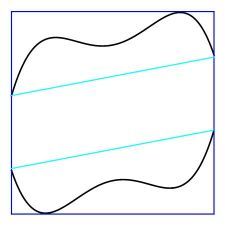
Here, the blue arc a the entrance to the small square is not tangent to the sides of that small square. Expanding it to the red semicircle b will result in a drop in B A , not an increase. The red semicircle b has a total angle of 1 8 0 degrees, while the blue arc a has a total angle of about 1 5 4 degrees. The drop in the ratio is very tiny but very real, from 0 . 5 1 2 7 to 0 . 5 1 2 5 . But in fact, the optimum figure has that red semicircle b right where it is, not touching the top of the small square, but with 3 identical cyan c quarter rounds in each of the 3 corners of the large square. The maximum ratio possible here is 0 . 5 3 3 9 . This is an example of where intuition fails , thinking that "the balloon inside expands to touch all sides of the exterior boundary", assuming that all the corners are truncated by quarter rounds will lead to the optimum ratio. It does not. An interesting consequence of this is that the exterior boundary doesn't necessarily have to be a closed figure, for an unique solution with maximum ratio to exist.
Thank you for an illuminating explanation. Whilst I got this right there is still a little part of me that thinks there should be a cycloid curve which is better. However I then imagine this shape being 'pumped up' whilst the perimeter is inextensible. I reckon it will fit to the sides and then join the side with a quarter circle arc.
Oh! I appreciate your enthusiasm but can you be a bit brief, please!!!. Please don't take this as an i n s u l t
Log in to reply
Look at Pedro Cardosa's solution for a brief, if incomplete, explanation. I would say most people solve this problem by assuming that the corners of the squares are truncated with identical quarter rounds. I haven't even established that with my not-brief proof!
i was thinking of solving it using variational calculus. it is better to think of simpler ways of solving this problem. i think you can compete it with little more effort.
Log in to reply
"...with little more effort." (!) Still can't complete it.
Log in to reply
You gotta write a wiki page on this!!! This would be of great use
[This is not a complete solution. It suggests that the answer isn't 25, to starve off reports claiming the answer is 25.]
Most people think because "for a given perimeter, the circle encloses the most area", hence we must use a circle to maximize the ratio.
Using a circle of radius 50, we calculate the ratio
2
π
r
π
r
2
=
2
r
=
2
5
.
The fact that we get the same ratio by using the large square should suggest that this reasoning isn't completely correct and that the ratio can be optimized further.
What is wrong with this reasoning?
Note: I do not have a rigorous proof of the actual answer, and I might be incorrect (though I believe this is indeed the correct answer).
If you can get a higher ratio than 26.508, please let me know! (Go ahead and report the problem!)
@Michael Mendrin Glad to know you arrived at this value. Though, I'm guessing you made an assumption about the general shape (which I did).
Log in to reply
There is a proof for this, which I'll try to put together. It'll rely on the fact that any curved section of any shape with maximal A/P (with constraints) is always an arc of a circle. I can offer an intruitive but not a fully rigorous proof for that one.
Log in to reply
This is the intuitive answer I arrived at as well. That it's an arc is not the surprise. What I wonder is why the arc must end at a tangent to the straight side.
Log in to reply
@Jeremy Galvagni – yeah, why? If you put air in a balloon inside a box, of course it's going to be all tangent to everything. But mathematicaliy explaining this is another matter. As I said, it's closely related to, but not the same as the Isoperimetric problem.
@Calvin Lin You explain great sir.
Here is something interesting ( ? ) : The maximum equals r ( radius of the circular arcs ) ...
Log in to reply
I'm not quite sure what you're trying to say. Can you elaborate? The comment seems incomplete.
Log in to reply
What I'm trying to say is this : The maximum ratio A/P is s/(2+sqrt(Pi)) where s is the length of the side of the square . And we get it when r = s/(2+sqrt(Pi))
Log in to reply
@Joel Petitet – Ah yes, the hard part is to prove this rigorously (which I currently do not have a good handle on).
If we restrict ourselves to "quarter-circle cutouts of the corners", then the maximization by calculus is the easy step.
I got this problem wrong yet my answer was taken as correct. I also assumed that the solution should be circular arcs and segments but for some reason, I kept the circular arc centers at the center of the square. I solved numerically and got 26.3432 which is close but not correct. I think on a second try I would have gotten there on my own but the solution was given to me, Brilliant is too flexible on the rounding of solutions for problems like this one, it could be customizable when one writes a problem.
Log in to reply
At any level for the error margin, we're going to have false positives (incorrect approach, misread question) and false negatives (calculator error, used different numerical values, etc). We accept decimal answers to a 3% degree of accuracy, which we feel is good tradeoff. This is standardized across the site, so as to avoid the complexity of "make sure your answer is within X% degree of accuracy and that you're using g = 9 . 8 exactly."
There are several ways we could phrase the question to enforce a tighter degree of accuracy, e.g. asking for ⌊ 1 0 0 × ratio ⌋ , though this introduces additional complexity in the problem statement.
Calvin, I tried, I still don't have a rigorous proof for the general case, showing that the optimal figure must have a perimeter that is parts of the exterior boundary and parts circular arcs that are tangent to it. I probably will have to try a different approach.
Log in to reply
Yea, for this style of problems, that's not too surprising to me. There is no "fundamental ideology" of why a (nice) solution should exist. E.g. if we changed the condition to maximizing (say) P 3 A 2 , I might believe that "wall of figure + circular arcs" still hold, but not necessarily "tangent to walls".
I didn't have high hopes that there is a rigorous solution to this problem. It felt interesting and engaging to get started with, and also has a really nice guessable "solution".
I still believe there could be a magic function which could give a higher value for A/P though I couldn't find one yet. I tried going for curves of the form |x|^n + |y|^n = 50^n. When n is 2 it give this circle. When n is very large, it gives the square. For some intermediate n it actually increases so it must give a maximum. And a maximum it gave at about n=4.4, with an A/P of 26.43143 which is still lower than 26.508 :(
Here is the table for the values I tried:
n A/P
1 17.67766953
2 25
2.5 25.82160227
3 26.19184723
3.5 26.3565824
4 26.41997434
4.1 26.42534438
4.2 26.42889524
4.3 26.43080766
4.4 26.43143389
4.5 26.43070384
4.6 26.42900009
5 26.41345261
6 26.34183871
7 26.25502805
8 26.16919588
9 26.08959076
10 26.01768417
inf 25 (square)
So the class of functions |x|^n+|y|^n=50^n does not work. But I still believe there exists a 'sweet' function that can do better. :) (Sorry for the bad formatting of the table, couldn't get any options)
Log in to reply
You might try some power around 4.4 but more like the currently best known: Flat at the sides and curved at the edges.
Log in to reply
Tried that. Turns out it gives the best ratio when it is the entire curve and not with flat + curves. That is anyway lesser than the solution though, so no go here :/
I got higher than 26.508. I got 27.609.
I figured the shape should be the intersection of the square, and a circle of radius r. I then used a numerical solver to determine the optimal r (it was 58.348) which yields a ratio of 27.609.
It's conceivable there's something wrong with my solver, but I don't believe so. I've replicated the answer several times, starting from scratch.
Log in to reply
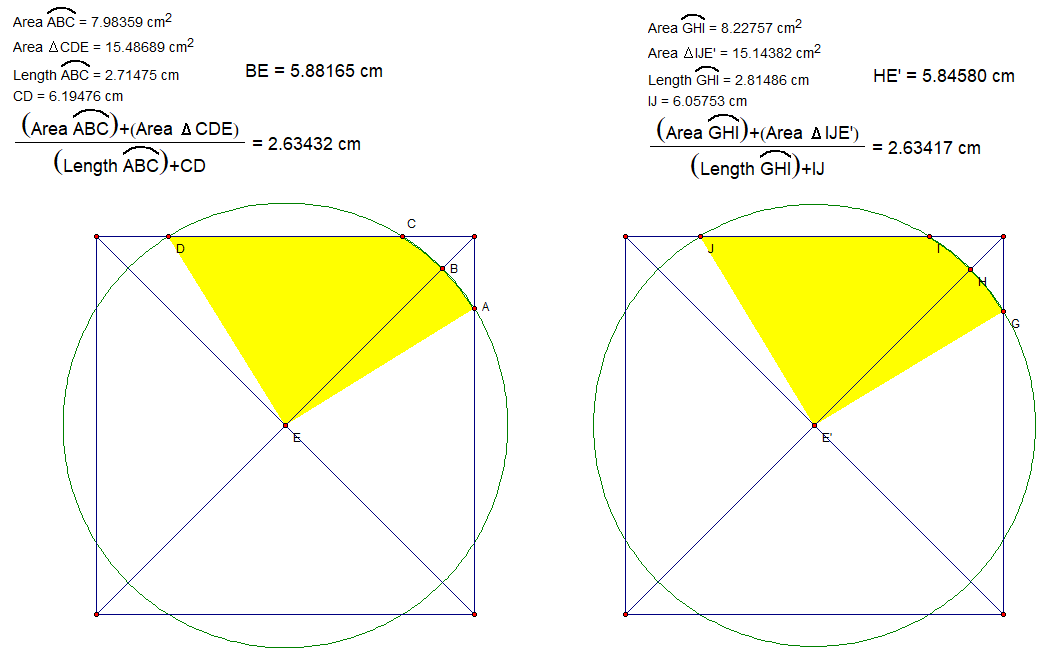
There were done hastily. The square is 10cm on a side so solutions must be multiplied by 10.
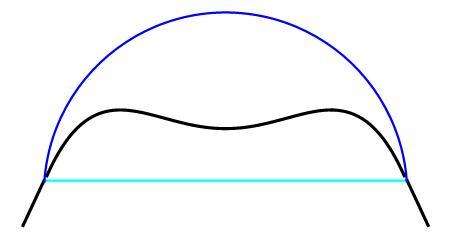
I did my best to maximize the ratio on the left. I used your radius on the right and the ratio is slightly smaller. Neither is as good as the current solution.
Can you share a picture of what you did or at least some formulas?
Log in to reply
https://tinyurl.com/y7pjugku
Log in to reply
@Matthew Bloomfield – My shape is only subtly different from the suggested shape. The key difference is that, I don't require 90 degree arcs in the corners. The suggested solution is essentially 4 quarter circles, joined together by rectangles. My solution is instead, a single circle that gets truncated by the edges of the square. So there's much less than 360 degrees worth of circular arc length. The corners are much less curved, in my solution, which allows a better trade-off between area and perimeter.
Log in to reply
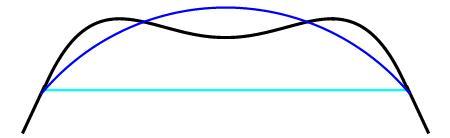
@Matthew Bloomfield – Here's a closeup picture of my shape versus the recommended shape. I'm zoomed in on Quadrant 1, but it's symmetric so it shouldn't matter:
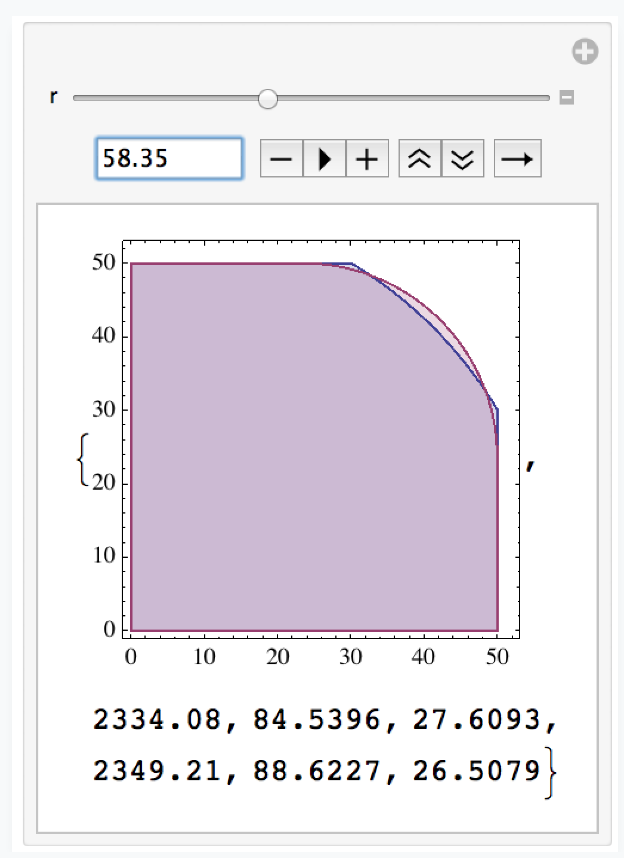
As you can see, the two shapes are very similar, but mine has a flatter corner. The result is that mine holds less area, but has a significantly shorter perimeter. There are two trios of numbers below the image, the top row is the area, perimeter and ratio for my shape (only quadrant one, so multiply the first two by 4 if you want the whole shape). The second row is the area, perimeter and ratio for the recommended shape.
Log in to reply
@Matthew Bloomfield – Matthew - I can't understand how your shape differs from the one offered by Jeremy? His corners are not quarter circles. It is a circle truncated by the sides of the square just as yours is. When you do this you need to find the optimal sized circle which as far as my equations tell me is the same as Jeremy's and I get the same answer. How does your numerical solver work? Presumably you need to put equations into it first. Can you share them? I am intrigued to see if you have beaten the answer. Many thanks. Simon
@Matthew Bloomfield – If the blue arc is from a circle centered at the origin then I think your numbers are just wrong. (It is possible mine are wrong. I have no reason not to trust geometers sketchpad.)
Looking at my two pictures their areas are 23.47048 and 23.37139 but you report a very slighty lower 2334.08 (Ignore the position of the decimal as my drawing is at 1/10 scale)
Comparing perimeters by my pictures are 8.90950 and 8.87239 but you report a much lower 84.5396
The ratio checks out. I will do some hand calculations to try to rectify our figures.
Log in to reply
@Jeremy Galvagni – Yea, I didn't get the perimeters to match up either. There isn't much more we can do without further clarification of his numerical solver.
@Matthew Bloomfield – I found your mistake. When you computed the length of the blue arc you used the radius of 50 instead of 58.348 but when you found the area you used the correct value.
Log in to reply
@Jeremy Galvagni – You might be right! I'll check it when I get home tonight :)
@Matthew Bloomfield – It's late here, but it's hard to figure out what's going on in your picture.
I think you're right.
For any given radius R ( With 50 <=R <= 50
sqrt(2) )
If x=angle(AEC) then A/L=25
(cos(x)+x))/(cos(x)+x*cos(Pi/4-x/2)) < 2.65 ( for 0<=x<=Pi/2 )
Am I wrong ?
Presumably, you're using the circle x 2 + y 2 = r 2 and intersecting it with the square with sides x = ± 5 0 , y = ± 5 0 , and the maximum is achieved when r = 5 8 . 3 4 8 .
For an explicit calculation, using the notation as in Jeremy's image, we have
C
=
(
r
2
−
5
0
2
,
5
0
)
,
∠
C
E
D
=
2
tan
−
1
5
0
r
2
−
5
0
2
,
∠
A
E
C
=
2
π
−
∠
C
E
D
.
Area
=
[
C
E
D
]
+
[
A
E
C
]
=
r
2
−
5
0
2
×
5
0
+
2
1
×
r
2
∠
A
E
C
.
Perimeter
=
C
D
+
A
C
=
2
r
2
−
5
0
2
+
r
×
∠
A
E
C
.
Setting r = 5 8 . 3 4 8 , we get r 2 − 5 0 2 = 3 0 . 0 7 , ∠ C E D = 1 . 0 8 , ∠ A E C = 0 . 4 8 8 , Area = 2 3 3 4 . 1 9 , Perimeter = 8 8 . 6 1 5 . Area/Perimeter = 2 6 . 3 4 .
Where we disagree is thus in the perimeter of your shape, where you claim it is 84.5396. Can you recheck? Did I misinterpret "intersection of the square, and a circle of radius r"?
This value of 26.34 is (close to) the maximum under this scenario of a central circle intersecting with a square, as remarked by Jose Fernandez Goycoolea in the comments of this solution.
I absolutely don't have a rigorous proof. Having thought about the problem some more I realised that there were two aspects of the problem:
1) What shape is made when 100 π < perimeter < 400.
2) What is the best ratio for such a shape given the end cases, circle and square, are both 25 ratio, and a trial of perimeter 200 + 50 π gives a ratio > 25.
1) To my mind the answer comes not from imaging a rubber band but asking what shape would a flexible but in-extensible 'strap' take up when pressurised. I.e If you have such a loop of thin strong metal measuring 350mm, what shape would it be? After some thought, imagination and symmetry I concluded the shape is likely to be the containing square with rounded corners.
2) Solved by calculus to give answer.
The same question can be asked for any regular polygon. I did it in my solution for an equilateral triangle. Surprisingly the triangle itself maximizes the ratio and the result is 14.43.
Log in to reply
Actually, I just now checked the case of an equilateral triangle of side length 100. The maximum ratio is 16.24, and the radius of the circular arcs tangent to the sides is 16.24 also.
Note: If you're feeling particularly serious, skip to the last line of my solution
By the 2D Isoperimetric Inequality, we have 4 π A ≤ P 2 so by rearranging, P A ≤ 4 π A . Since A obviously is maximized when we enclose the whole square, we have P A ≤ 4 π 1 0 0 2 ≈ 2 8 . 2 1 and finally since we know the square itself gives A / P = 2 5 , the maximum must satisfy 2 5 . 0 0 ≤ A , P max P A ≤ 2 8 . 2 1
Therefore all we have to do is test all 2 8 2 1 − 2 5 0 0 + 1 = 3 2 2 possible answers to two decimal places to find the answer is 2 6 . 5 1 !
Yes, while the math is completely correct, this solution is my idea of a joke (Hopefully that's okay, Brilliant staff?). Feel free to comment, but please don't upvote it. Go read one of the other solutions and upvote them--they put a lot of effort into their solutions.
There's got to be some way to make use of the inequality relation that you have, let me think about it. An upvote for your bringing it into attention.
My solution is similar to Pedro Cardoso's solution. Instead of a rubber band, I imagined the behavior a soap bubble. It could be summarized for any regular polygon. For example, it can be done for an equilateral triangle. As the soap bubble becomes bigger and bigger and reaches the sides of the triangle, its base( initially a circle) will try to cover maximum area, and minimize its perimeter. The circle(base) will flatten along the three sides of the triangle, and at the corners will form arcs, each one a third of a circle, as shown in the drawing bellow. Surprisingly, the ratio this time is maximized by the triangle itself.
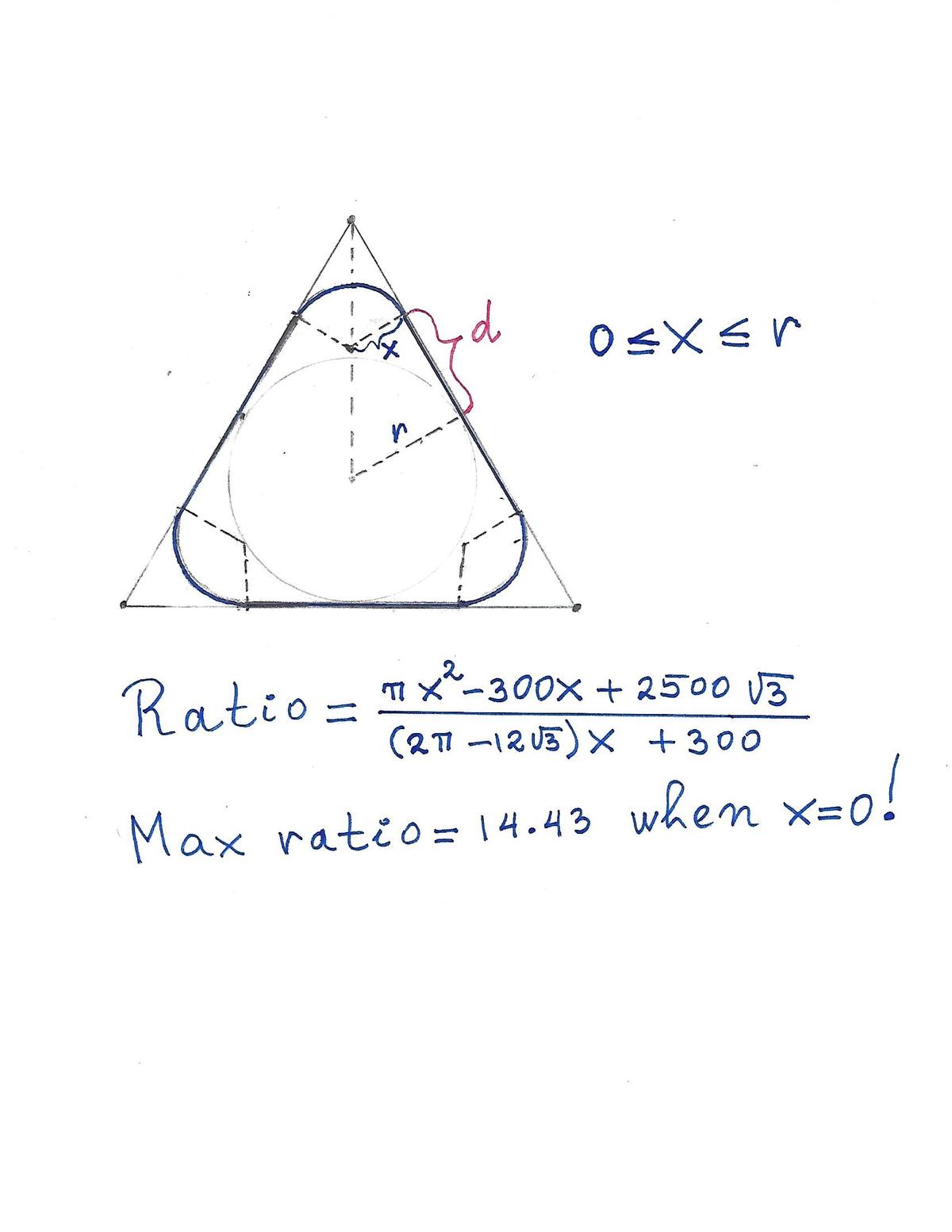
Actually, I just now checked the case of an equilateral triangle of side length 100. The maximum ratio is 16.24, and the radius of the circular arcs tangent to the sides is 16.24 also.
Log in to reply
I used an intuitive approach, and it looks like I'm wrong.
Log in to reply
What I find curious is that in the case of maximum ratio, P A = r , regardless of what polygon is the exterior boundary, if the interior angles are the same. Edit: Apparently, sometimes even when the interior angles are not the same. For an irregular pentagon formed of an unit square with a right angle isoceles on top, all the radii are the same, 0.235144, which, once again, is the maximum ratio.
Started with a triangle inscribed inside the 100x100 square and found ratio of A to P to be about 15.5.
The square, octagon, circle all have ratios of A to P of 25. Intuition says it must be a combination of shapes that would yield ratio higher than 25. It would most likely be a square with rounded out corners. It is not likely to be a rounded out larger n-gon because this shape would have a ratio close to that of a circle. Wouldn’t make sense to have any concave polygons either since area would be small.
Rounding out the corner of a square with varying radii from 1 to 50 and checking the ratio of A to P in between we find corner radii 26 and 27 both yield a ratio of 26.51. As we round out the square to make it change from a square to a circle, the ratio follows a parabolic path.
Wow, that's really interesting that the octagon has a ratio of 25 too. I certainly didn't expect that. Maybe there's an interesting question about what kinds of "maximal shapes (IE touching all 4 sides so you can't scale further)" have such a ratio.
Note: I believe the path isn't parabolic, but that depends on how you parametrized the function.
I think most people ended up with something like
A
x
+
B
+
x
C
, which could look like a parabola when focused within a small interval.
Imagine a square box of side 1 0 0 . then, imagine that there is a rubber band constraining a gas (suppose the rubber band doesn't let the gas pass through)
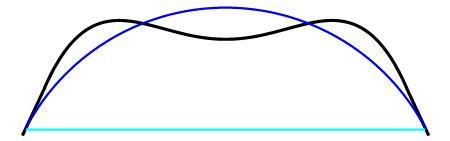
This is exactly the kind of setup we need, as the rubber band tries to minimize its length (perimeter), and the gass tries to maximize its volume (in this case, area).
If you start blowing more gas into the rubber band's confinments, it will initially be a circle, until the rubber band starts hitting the walls of the container, then it becomes 4 circular arcs of 90 degrees, connected by line segments
The ratio is Perimeter Area = 4 0 0 + ( 2 π − 8 ) x 1 0 0 2 + ( π − 4 ) x 2 .
The maximum value of this function is 2 6 . 5 0 8 .