Maximum Ball

Geometry Level 2

What is the value of the dimension $n$ that maximizes the volume of unit $n$ -ball $\left\{ \left( x_1,x_2,\cdots,x_n \right) \in\mathbb{R}^n\, \mid \, x_1^2+x_2^2+\cdots+x_n^2\le 1 \right\}?$

Hint: The volume of $n$ -ball of radius $R$ is $V_n(R)=\frac{\pi^{\frac n2}}{\Gamma \left(\frac n2+1\right)}R^n,$ where $\Gamma(\cdot)$ denotes the gamma function .

The answer is 5.

4 solutions

Brian Moehring
Aug 3, 2018

Using the hint, $\frac{V_{n+2}(1)}{V_n(1)} = \pi\frac{\Gamma(\frac{n}{2}+1)}{\Gamma(\frac{n}{2}+2)} = \frac{\pi}{\frac{n}{2}+1} = \frac{2\pi}{n+2}$ so that $V_{n+2}(1) < V_n(1) \iff \frac{2\pi}{n+2} < 1 \iff n > 2(\pi-1) \approx 4.28$

This means we only need to check which is the larger of $V_5(1)$ and $V_6(1)$ : $\frac{V_5(1)}{V_6(1)} = \frac{16}{5\pi} \approx 1.019$ so $V_5(1)$ is larger, so the maximum volume occurs when $n = \boxed{5}.$

What's an easy way to show that $\dfrac{V_5(1)}{V_6(1)}=\dfrac{16}{5\pi}$ , without directly using the formula for the volume in terms of the Gamma function?

I suppose that we can start with $V_1=2$ and $V_2=\pi$ and work from there, using your ratio formula for each of the odd and even dimension series.

Michael Mendrin - 2 years, 10 months ago

Personally, I just used the given formula along with $\Gamma(x+1) = x\Gamma(x)$ and $\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}.$

It's not especially easy, but you can do this if you want to avoid using that formula:

First define $B_n(r) = \{\mathbf{x} \in \mathbb{R}^n : |\mathbf{x}| \leq r\}$ and then $\begin{aligned} V_{n+1}(1) &= \int_{\mathbf{x} \in B_{n+1}(1)} d\mathbf{x} \\ &= \int_{-1}^1 \int_{\mathbf{x} \in B_n(\sqrt{1-y^2})} d\mathbf{x}\,dy \\ &= \int_{-1}^1 V_n(\sqrt{1-y^2}) \, dy \\ &= V_n(1) \int_{-1}^1 (1-y^2)^{n/2} \, dy \\ &= 2V_n(1) \int_0^1 (1-y^2)^{n/2} \, dy \\ &= 2V_n(1) \int_0^{\pi/2} \cos^{n+1}\theta \, d\theta & \text{using } y=\sin\theta \end{aligned}$ so that $\frac{V_6(1)}{V_5(1)} = 2\int_0^{\pi/2} \cos^6\theta\,d\theta$ which comes out to (by whatever your favorite method is) $\frac{5\pi}{16}.$

Brian Moehring - 2 years, 10 months ago

Brian, I asked for a easy way. But I've just now posted a continuation of your easy solution.

Michael Mendrin - 2 years, 10 months ago

@Michael Mendrin – I consider "easy" to mean "any student learning multi-variable calculus could do it". Obviously the formula using the gamma function wouldn't necessarily be accessible to such a student, but the method I've shown should be, even if it's a little longer shrugs

Brian Moehring - 2 years, 10 months ago

Does it make sense to claim that that 2 meter is less than 3.14 square meter?

Bo Jacoby - 2 years, 9 months ago

No, but it does make sense to claim that $2$ is less than $\pi,$ and that's all that matters, as the radius is unitless in the context of this problem.

If you're unwilling to accept a unitless radius, then you can just consider the problem as comparing coefficients $k_n$ where $V_n(R) = k_n R^n$

Brian Moehring - 2 years, 9 months ago

Michael Mendrin
Aug 12, 2018

Using Brian Moehring's formula for the ratio of $V_{n+2}$ and $V_n$ , and using the fact that $V_1=2$ and $V_2=\pi$ for unit radius, then the series for odd and even dimensions are, for unit radius

$\dfrac{4^n n!\pi^{n-1}}{(2n)!}= \left( 2, \dfrac{4\pi}{3}, \dfrac{8\pi^2}{15}, \dfrac{16\pi^3}{105}, \dfrac{32\pi^4}{945},... \right)$

$\dfrac{\pi^n}{n!}=\left( \pi, \dfrac{\pi^2}{2}, \dfrac{\pi^3}{6}, \dfrac{\pi^4}{24}, \dfrac{\pi^5}{120},... \right)$

the maximum being $\dfrac{8\pi^2}{15}=5.26379...$ for a 5-ball

For $n=2$ , it's easy to see that the following works out to $\pi$

$V_n=\dfrac{\pi^{\frac {n}{2}}}{\Gamma \left(\frac {n}{2}+1\right)} =\dfrac{\pi^{\frac {2}{2}}}{\Gamma \left(\frac {2}{2}+1\right)} =\pi$

However, for $n=1$ , the result of $2$ depends on the fact that

$\Gamma(\dfrac{1}{2}) = \sqrt{\pi}$

and making use of the identity

$\Gamma(x+1) = x\Gamma(x)$

Here's the plot of the volume function for any real value $n$ , the dotted red being the maximum for any integer $n$

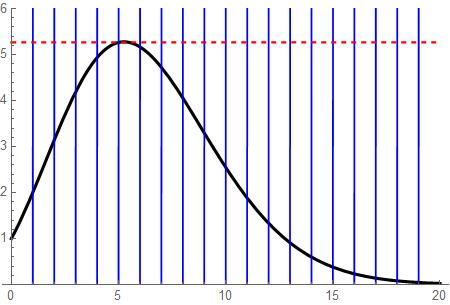
Alternatively, note that $V_2(1) = \text{Area of circle with radius } 1 = \pi \times 1^2 = \pi \\ V_1(1) = \text{Length of the interval } [-1,1] = 1 - (-1) = 2.$
One would need to show these are identified with the given formula when proving it, but there's no need to use the given formula to find them.

Brian Moehring - 2 years, 10 months ago

Right. But the point is, it seems unavoidable to treat the odd and even series seperately. Mind if I borrowed another one of your formulas again?

Michael Mendrin - 2 years, 10 months ago

Go ahead. I have no plan on patenting any of them ;-)

Brian Moehring - 2 years, 10 months ago

@Brian Moehring – Here's a challenge for you: Is it possible to express these coefficients of $V_n$ without resorting to either Gamma functions or factorials of half integers? I've given formulas for each of the odd and even series, can they be combined with a single expression as a function of dimension?

Michael Mendrin - 2 years, 10 months ago

@Michael Mendrin – Are you just asking whether we can write functions $f : \mathbb{N} \to \mathbb{R}$ of the form $f(n) = \begin{cases}a(k) & n=2k \\ b(k) & n=2k+1 \end{cases}$ without using cases?

If so, then the answer is "definitely," but the methods I know for doing this are rather brutish and result in a formula that is often less useful than using cases. It looks something like $f(n) = \frac{1 + (-1)^n}{2} a\left(\left\lfloor\frac{n}{2}\right\rfloor\right) + \frac{1 - (-1)^n}{2} b\left(\left\lfloor\frac{n}{2}\right\rfloor\right)$

Feel free to tell me if I've misunderstood.

Note: if you want to disallow explicit use of the floor function, just note that $\left\lfloor\frac{n}{2}\right\rfloor = \frac{n}{2} - \frac{1-(-1)^n}{4}$

Brian Moehring - 2 years, 10 months ago

@Brian Moehring – Yeah, already tried that, and, yes, the result looks horrible. I've been aware of the distinct odd and even series for these coefficients for some time now, and yet they wonderfully seem to be able to hang together nonetheless. It's a remarkable series. You might want to see How To Construct a 4D Menger Sponge and see how the Wallis formula can be generalized.

Michael Mendrin - 2 years, 10 months ago

@Brian Moehring – I should mention that the approach you've suggested still result in factorials of half integers anyway.

Michael Mendrin - 2 years, 10 months ago

@Michael Mendrin – Not so. You have given functions for even/odd parity separately which doesn't use factorials of non-integers. My approach, while practically useless, always inputs non-negative integers into your two functions, so it never requires use of the factorial of anything other than a non-negative integer.

Brian Moehring - 2 years, 10 months ago

@Brian Moehring – Let me look at my files and see the full formula expressed in this way.

$\dfrac{\left((-1)^n+1\right) \pi ^{\frac{1}{4} \left(2 n+(-1)^{n+1}+1\right)}}{2 \left(\dfrac{1}{4} \left(2 n+(-1)^{n+1}+1\right)\right)!}+\dfrac{\left((-1)^{n+1}+1\right) (2 \pi )^{\frac{1}{4} \left(2 n+(-1)^{n+1}-3\right)}}{\left(\dfrac{1}{2} \left(2 n+(-1)^{n+1}-1\right)\right)\text{!!}}$

Well, it's not very edifying, so I've never published it. But I see your point about the factorial denominators.

Michael Mendrin - 2 years, 10 months ago

Vinod Kumar
Aug 12, 2018

Simply evaluate the Volume expression for R=1 for n=1,2 ... 7 and find it is maximum at n=5.

I'm getting the volume at n=5 to be 8.747, and the volume at n=7 to be 9.160. Where am I going wrong?

Scott Rudell - 2 years, 10 months ago

Which exact expression are you using to compute those values? And if it involves the gamma function, which values are you using for those things?

C . - 2 years, 9 months ago

Supriya Manna
Aug 18, 2018

Just go beyond of 4

Maximum Ball

The answer is 5.

4 solutions

0 pending reports