Maximum Charge
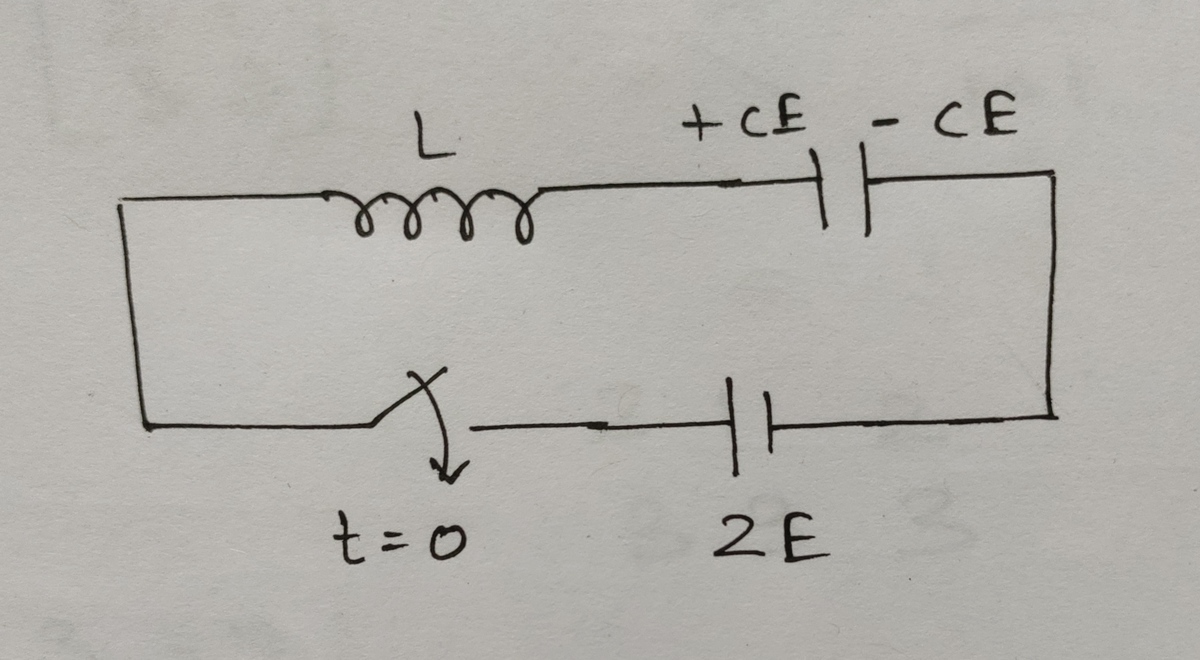 Initially the inductor is de-energized at
t
=
0
and the capacitor has a charge of
C
E
at
t
=
0
Initially the inductor is de-energized at
t
=
0
and the capacitor has a charge of
C
E
at
t
=
0
Find the maximum charge on capacitor after the switch is closed.
Answer comes in the form of
α
C
E
Type your answer as
α
=
?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase Thank you so much sir
@Steven Chase you have solved through 2 method. Thanks a lot
Log in to reply
You're welcome. This was a good one for practicing both solution methods. I'm off to bed now
@Steven Chase
are you free? Or whenever you will be, please solve this

Thanks in advance. LYS
Log in to reply
Here is what I am getting. If it is right, I can post a note on it:
2 π ω 0 k S M
Log in to reply
@Steven Chase
Great people often make small mistake
The answer is
2
π
k
S
M
ω
0
@Steven Chase please share your attempt. LYS
Log in to reply
@Talulah Riley – I found my mistake. That will fix it. I will post in half an hour or so
@Steven Chase
sir I have evergreen doubt in one type of concept in SHM. Can you make a note on that.
I will share if you will say yes. you can make note tomorrow or whenever you will be free.
Hello, Talulah.... I've added an even simpler Laplace Transform solution in addition to Sir Steven's menagerie! Enjoy :)
Let q ( 0 ) = C E , q ′ ( 0 ) = 0 for this oscillator circuit. By Kirchhoff's Voltage Law, we have the differential equation:
L q ′ ′ ( t ) + C 1 q ( t ) = 2 E (i)
and taking the Laplace Transform of (i) gives:
L [ s 2 Q ( s ) − ( C E ) s − 0 ] + C 1 ⋅ Q ( s ) = s 2 E ⇒ Q ( s ) = s ( L s 2 + 1 / C ) 2 E + ( L C E ) s 2 = s 2 C E − L s 2 + 1 / C ( L C E ) s (ii)
and the inverse Laplace Transform of (ii) yields:
q ( t ) = ( C E ) ⋅ [ 2 − cos ( L C t ) ]
which has a maximum capacitor charge of q M A X = 3 C E .
Let the capacitor voltage be V C , and let the inductor current be I L . The governing equations for the circuit are:
2 E − V C = L I ˙ L I L = C V ˙ C
Substituting the second equation in to the first yields:
2 E − V C = L C V ¨ C
The homogeneous equation is:
V ¨ C = − L C 1 V C = − ω 2 V C ω = L C 1
The homogeneous solution is sinusoidal, and then we must add a constant term as well.
V C = A sin ( ω t ) + B cos ( ω t ) + D V ˙ C = A ω cos ( ω t ) − B ω sin ( ω t ) V ¨ C = − A ω 2 sin ( ω t ) − B ω 2 cos ( ω t )
Initial conditions:
V C ( 0 ) = E = B + D V ˙ C ( 0 ) = 0 = A ω V ¨ C ( 0 ) = L C E = − B ω 2 = − L C B
Solving for the constants yields:
A = 0 B = − E D = 2 E
Finally:
V C = − E cos ( ω t ) + 2 E
The maximum value of V C is therefore 3 E , and the maximum charge is 3 C E .
To solve numerically, we only need to consider the basic equations.
2 E − V C = L I ˙ L I L = C V ˙ C
Isolate the derivative terms and numerically integrate.