This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
sir what application did you use to draw the figure?
Log in to reply
I use Omnigaffle. It's not great for "accurate geometric construction", and you can see that the left tangent actually intersects the circle twice.
Log in to reply
Thanks for replying, I'll see if it's easier to use than Grapher :)
Notice the dotted circle between the two circles has a radius of 9cm. The circumference of this circle = 2pi r = 2pi 9 = 18pi The diameter of each small circle (to be inscribed) is 2.
18pi / 2 = 28.27 ~ = 28.
Thus 28 circles can be drawn.
In your explanation, the collection of 28 diameters of the inscribed circles make a polygon of 28 sides and not a smooth circle. The greatest difficulty is that if we draw two tangents from the original centre to the two sides of the inscribed circles, such a pair of tangents will not touch the opposite sides of the same diameter of the circle, but slightly below it .Only parallel tangents drawn on opposite sides can exactly touch the opposite sides of the same diametric line. So if I calculate the angle subtended by the small circle at the centre by trigonometrical operations and divide 360 by this, I get a number slightly more than real. For instance, I got mathematically 28.where as when I made a diagram it was only 27...So I wonder who can make a working model and attempt it!!!! For me, the real question is :Is it 27 or 28?
You have an approximation. How do you know that it's accurate enough to actually fit 28 circles? That is the difficult part of the problem.
For example, if we had an outer circle of 2.1 and an inner circle of 0.1, then the "circumference of the dotted circle is 2 . 1 π × 1 = 2 π ≈ 6 . 3 and the diameter of the small circle is 2, and your approximation will say that we can fit in 2 6 . 3 ≈ 3 . 1 5 circles. However, we can only fit in 2 of these unit circles.
Log in to reply
No, i did not get exact 28, but with some decimal values, which is avoided since number of full circles are asked :) Regards :)
Let us place the unit circles in the annulus touching each others so as to maximize their number. After the last unit circle, there may or may not be some space left. Now, the center of concentric circles together with centers of two adjacent unit circles would form an isosceles triangle with sides 9, 2 and 9. The angle 2x opposite to side of length 2 in this triangle, subtended at the center of concentric circles, would have the value such that,
Sine(x) = 1/9.
When the centers of adjacent unit circles are joined, a polygon of side length 2 each would be formed. The length of the last side of polygon would be 2 or a little bit more than 2.
The circumference of the circle joining centers of unit circles would be 2π×9=18π, the radius being 8+1=9. This can not accommodate more than 28 unit circles, as 18π÷2 = 9π = 28.274 < 29.
If 28 unit circles get accommodated, the angle subtended at the center would not be more than 2x = 360/28, and Sine(x) would be 0.11196, and side length in a regular polygon would not exceed 2×9×(0.11196) = 2.01536.
Total perimeter, 2.01536 × 28 = 56.4301, which is less than the circumference 18π = 56.54866.
As such 28 unit circles can be accommodated leaving negligible Vacant space.
it is wrong that the two tangents make an isosceles triangle along with the diameter of the small circle because such tangents drawn on either side of the diameter will run parallel and would not meet. So we have to consider a line just below the diameter somewhat smaller.
While there are some interesting ways to solve this problem as I have seen below, I believe that there is a way to solve this problem with only simple mathematic skills. First, I shall call the area between the circle with the radius 10 and the second circle with the radius 8 "Area S"
Let us imagine that there are 4 unit circles, which are in equal distances from the neighbouring two (so if the 4 centres are connected, the connecting lines would form a square), situated in "Area S", as shown in the picture above (in the question). Since circles are symmetric shapes, the number of unit circles that fit into "Area S"between the upper unit circle and left unit circle will be the same as that of circles that fit in between the left unit circle and the bottom unit circle, that of circles between the bottom and the right and that of circles between the right and the upper unit circle. Therefore, the total number of unit circles that fit between the first 4 unit circles in "Area S" should be divisible by 4. We have the possible choices 26, 27,28, 29. If we deduct 4 (from the first 4 unit circles), we get 22, 23, 24, 25. Amongst these numbers, only 24 is divisible by 4, so we have out answer: 28.
While the explanation of this method does seem lengthy, if you grasp the concept, it should seem much easier than the methods using trigonometry. Thank you for your time.
That's a huge assumption that "we must have 4 circles placed in a symmetric square". If that were the case, why couldn't "we must have 3 circles placed in an equilateral triangle" and hence conclude that the answer is a multiple of 3? In fact, it is not always true that the answer is a multiple of 4, which you can verify by thinking of the circles as slowly expanding / contracting. For example, if the outer circle has radius 2.1 and the inner circle has radius 0.1, then we can only fit in 2 circles.
Log in to reply
Yes, I see what you mean. Thank you for pointing out the fault.
Imagine one such circle whose raius =1cm Imagine a right angled triangle, having its origin at the common centre of the two circles with the radius of the small circles (1cm) as opposite side, adjacent side being of length (8+1) =9cm. Then tan of angle = Opposite side/ adjacent side= 1/9; so angle = tan^-1(1/9) =6.34degree; each small circle makes 2x 6.34 = 12.68 degrees at the centre. If x circles can be placed, they together makes 360degrees at the centre. so no.of such circles = 360/12.68 = 28.38; so number of full circles that can be placed =28
Unfortunately, this argument still doesn't hold, because the right angled triangle still doesn't cover the entire unit circle, so we do not know for certain that the circle can be placed.
Once again, taking the extreme example where the inner circle has radius 0 and the outer circle has radius 2, we obtain that the right angled triangles are 1 − 1 − 2 and hence have an angle of 4 5 ∘ . Then each small circle "makes" 2 × 4 5 ∘ = 9 0 ∘ at the center. You then claim that we can place 9 0 3 6 0 + 4 full circles, while it's pretty clear that we can only put in 2 circles.
Here is the image. Even though we can fit in the blue and green right triangles, we cannot fit in the blue and green circles.
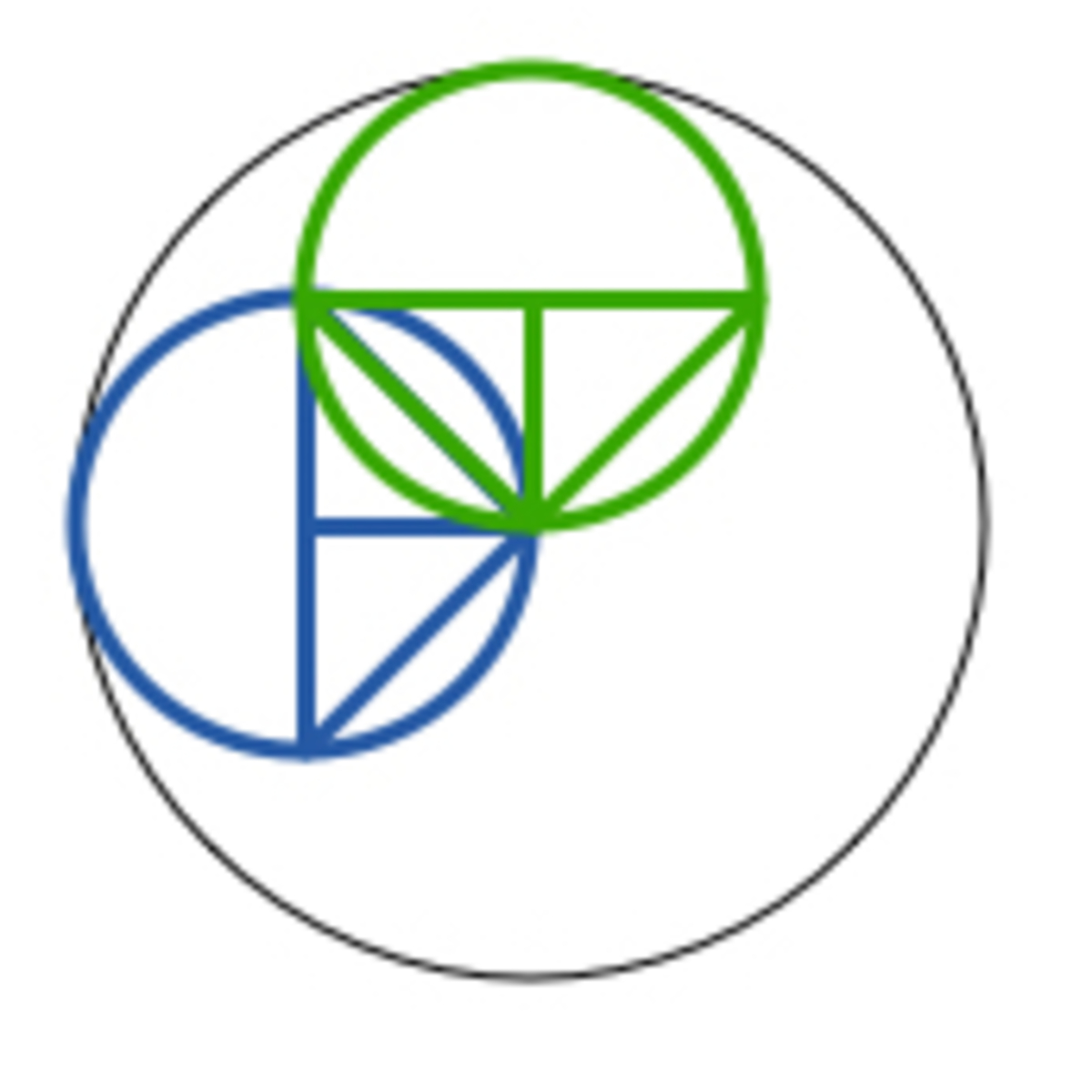
Log in to reply
I really appreciate your point and approve fully to that; your argument may be concluded as this; the hypotenuse we draw for the triangle is not tangential but crosses the circle, which become more and more prominent when the inner circle is getting smaller, and this becomes much evident when the inner circle takes the radius of zero as you have spotlessly proved. I am not at all unhappy that I am proved wrong, but happy that there is more to understand deep; thank you very much
PS: two tangents drawn at the opposite ends of the diameter of a circle must run parallel and would not meet at the centre of the circle but at infinity. That is the basic reason for my explanation having gone wrong!!!
Log in to reply
Right, so the step of "which becomes more and more prominent" has to be properly justified.
You are actually very very close to the correct approach. Think about what "right angled triangle still doesn't cover the entire unit circle" really means, and how we can fix that issue. E.g. in my image, the angle that we want to calculate is 1 8 0 ∘ instead of 9 0 ∘ . If we did that, then we can easily see why the answer is 1 8 0 3 6 0 = 2 .
Log in to reply
@Calvin Lin – In my explanation, i was trying to find the angle subtended by each circle at the centre and then dividing 360 with this angle to get the number of such circles that can be drawn around. In your example of biggest inscribed circle, the two tangents drawn will be extended on either side along the diameter making an angle 180 degree; then we easily conclude the maximum number of circles =360/180 =2. So the real problem is to decide what angle a pair of tangents will make at the centre of the circle. If your argument is accepted for every circle about 2x 12 68 degrees must be reserved for each circle; so numbers of circles = 360/(2x12.68) = 14, rounded off; did you mean that way? For a better understanding, i made an approximate diagram; i found that only 27 circles and not 28 could be included fully.

Log in to reply
@Nanda Kumar – Great! That is indeed the argument that we want. The circular sector that we're creating has an angle of 2 sin − 1 9 1 (whereas the previous one that you used had a slightly smaller angle of 2 tan − 1 9 1 . Hence, the number of circles will be ⌊ 2 sin − 1 9 1 2 π ⌋ which is equal to 28 (courtesy of Wolfram). So, in fact, 28 circles can indeed be done.
Can you update your solution accordingly?
FYI To display an image, we use the markdown notation of

. I've edited your comment so you can see how that works.
Log in to reply
@Calvin Lin – But sir, only 27 full circles can be included; 28th is only partial :)
Log in to reply
@Nanda Kumar
–
Because
2
sin
−
1
9
1
2
π
=
2
8
.
2
1
6
, you have very little wriggle room.
With a visual, you do not know how tangent your circles are, and how much room for error you introduced between circles.
Did you understand how I came up with sin − 1 9 1 ?
Log in to reply
@Calvin Lin – ( I think we the hypotenuse is actually not the tangent, but the line connecting the original centre with the centre of any tiny circle, so that sin (theta) = 1/9; it is not tan(theta); right?
[url=https://flic.kr/p/HA2qzj][img]https://c5.staticflickr.com/8/7384/27295666132 4eed82aae9 k.jpg[/img][/url][url=https://flic.kr/p/HA2qzj]20160601_164128[/url] by [url=https://www.flickr.com/photos/flashbackr/]Nandakumar UK[/url], on Flickr
There is a formula for both area and circumference of a circle:
Circumference
The Circumference of a circle is basically the perimeter. You figure it out by multiplying the diameter by Pi. In this case it was:
3.14 x 16 = 50.24 for the smaller circle
Unit circles: 2 x 3.14 = 6.28
Area
The formula for this is: Pi by Radius squared.
Smaller circle: 3.14 x 8 squared = 200.96
Bigger circle: 3.14 x 10 squared = 314
Unit circles: 3.14 x 1 squared = 3.14
314 - 200.96 = 113.04
113.04/3.14 = 36
50.24/6.28 = 8
36 - 8
= 28
Unfortunately, you cannot just divide the area of the annulus by the area of the unit circles.
For example, if the larger circle had a radius of 2, and the smaller circle of very close to 0, then your area calculation would provide an answer of 3 (rounded down), but it's clear that we can only squeeze in 2 circles.
The reason for this is that the 28 is only an upper bound, and there is a lot of "lost area" that we're not making use of.
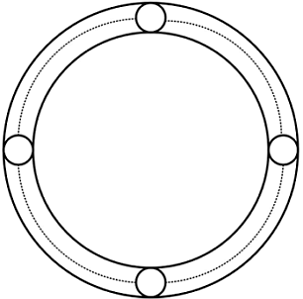
For each unit circle that we place, let's consider the central angle that is subtended. The radius of the unit circle is 1, and the distance from the center to the unit circle's center is 9. Hence, the purple angle is 2 sin − 1 9 1 .
It is clear that given any 2 unit circles, the central angle that they subtend will be distinct. Hence, this shows that we can have at most ⌊ 2 sin − 1 9 1 2 π ⌋ unit circles placed.
Conversely, if we split the large circle up into 28 sectors of central angle 2 sin − 1 9 1 (with one small sector leftover), we can place a unit circle into each of these sectors. Hence, 28 can be achieved.