Maximum Face Sum
The vertices of a cube are labeled with the numbers 0, 1, 2, 3, 4, 5, 6, 7 such that no two vertices are labeled with the same number. The sum of any 2 numbers on an edge is prime. What is the maximum sum of the 4 numbers on a face?
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Following your solution, I got the answer as 84
I have applied same solution.
As we can see from the question, sum of any 2 numbers on the edge is prime. Thus, it is better by fixing a number at a vertex. In this case, it is much convenient to fix 7 at a vertex [ I took the largest number 7 because, the probability of finding a prime number decreases with summation of positive numbers]. Now, seeing the numbers, only 4, 0, 6 can find their place beside 7. Fix the numbers 0,4,6 arbitrarily beside 7 now look at common vertex of 4 and 6 other than 7. Only 1 can fit there as the remaining digits [2,3,5] add up to composite numbers. Look at the common vertex to 4 and 0 other than 7, it can take the value 3 alone as the remaining digits [2,5] add up to composite numbers. Look at the common vertex to 1,3 other than 4, it is 2 as sum of the 2 numbers with 5 gives composite numbers. The leftover number is 5, place it in the left over vertex. since the frame of the cube is complete, add up the numbers of each face. the set we get is [18,14,10]. So, obviously the solution is 18
There isn't much flexibility in arranging the numbers, and so the configuration is quite fixed. By considering the largest vertex, we can quickly restrict the possibilities.
Log in to reply
I labeled my cube in this manner and got 22 as an answer. Still wrong?
0-1-2-3 on top
7-6-5-4 on bottom;
such that 0-1 on one edge, 1-2, 2-3, 3-0.
0-7, 7-4, 3-4, 4-5, 5-2, 5-6. We notice the sum of two vertices is prime.
I got the maximum Sum=22. Still wrong?
Log in to reply
Log in to reply
@Calvin Lin – No, 1 is not prime. Thanks, you are right, answer should be 18.
Hey ,how was JEE ? Expecting a Top 10 rank ? Vadodara's hopes rest on you ;)
Log in to reply
Hi! Haha not quite ;-) I did rather well in math and physics, but chemistry really took me down (you can easily guess, inorganic) according to provisional keys, my marks should be math 112, physics 116 and chemistry 68 so 296 which according to my teachers should land me at the AIR 500 range.(nothing can be said for sure) I'm quite happy regarding my performance though, I did well in what I knew and well inorganic chemistry was always going to be a game of luck for me, scoring there is for guys who work hard... Although my friend Anant Chhajwani is scoring 340-350 marks and is expected to be in the top 100, so Vadodara isn't completely unrepresented LOL. Tell me about you! How did it go? and how did others find the paper? I was (and am) in vacation partying mode so I dont know anything regarding it right now.. also can you tell me the names of discussions on brilliant where all this was discussed? Thanks a lot!
Log in to reply
Math and Chem were really easy for me .
-
Math : 108
-
Physics : 54 :(
-
Chem : 106
I know that my score is bad , so I haven't really participated in any post JEE discussions , though I had been mentioned in 2-3 notes .But don't worry , I'll try to find them .
And yes , there is @Ronak Agarwal , who's expected to be the topper from Brilliant , unless of course you beat him ;) .
EDIT: I used the Reso key . I'm a Reso DLPD student .
Log in to reply
@A Former Brilliant Member – Yes the resonance key seems to be the most accurate one...Good and bad is all relative; who knows what we'll do right? (Not to take anything away from Ronak's achievement, he really is awesome; this is an excuse we can use on ourselves ;-D)
Log in to reply
@Siddharth Brahmbhatt – All the best to you . Maybe I can get to meet you in the future , but for now I have to leave Brilliant since some people don't like having me here .
Cya!
Log in to reply
@A Former Brilliant Member – Oh come on! People can't bog us down! Anyway that is your decision, although i'd suggest you not to do so. Just tell me where you take admission alright? Maybe we'll meet in inter-iit! (already dreaming)
Log in to reply
@Siddharth Brahmbhatt – :) But , still it feels really bad if people think bad of you .
Btw my family's moving to Chennai in 2 years , so it's no use for me studying in the North ; I mean the traveling costs and other things will be more . So , I'll be joining IIT-M or VIT Vellore .
Sure! If that's the case I'll try to get into IIT-M itself .
You'll be here, so maybe I'll try to stay in touch thru B'ant itself .
eg: 0+[2,3,5,7] 1+[2,4,6] 2+[3,5,1,0] 3+[2,4,0] 4+[1,3,7] 5+[2,0,6] 6+[1,5,7] 7+[0,4,6] now see each vertices can have only other 3 neighboring vertices..... however we have an additional options for 0 and 2 But since 1,3 and 5 have to combine with 2 so we discard the association between 0 and 2 . So, we have formed the association and drawing the association into the cube we can find out the face with the largest sum is the combination of 1,4,6 and 7 and thus 18
0 cant be situated in such a vertex where 1 or 4 or 6's vertices are directly connected by a side as 0+1, or 0+4 or 0+6 is not a prime,so 0 could share sides with 2,3,5,7 ,but we have to keep in mind that one vertex is connected with exactly 3 sides, so we need optimization by analytical thinking.Likewise 1 must have three friends i.e. sides of vertex labelled by 2,4,6. For 2 there four vertices 0,1,3,5 would be neighbor of him,but we have to decide whose three are our poor 2's neighbor. Similarly for 3,only choices are 0,2,4. Similarly for 4,only choices are 1,3,7 Similarly for 5,only choices are 0,2,6 Similarly for 6,only choices are 1,5,7 Similarly for 7,only choices are 0,4,6 Now apply your imagination Peter,voila! This is now an easy task even for a second grader,as i am a professional engineer,imagination is nothing for me as i know how the potential energy of niagara falls water is used to blend the fruits in my blender
For 7 we have only 3 combinations 7+6 =13 7+0 = 7 7+4 = 11
For 5 we have only 3 combinations 5+2 = 7 5+0 = 5 5+6 = 11
For 6 we have only 3 combinations 6+1 = 7 6+7 = 13 6+5 = 11
Thus putting these in a cube we get the following faces of cubes 6,1,7,4 6,5,1,2 6,7,5,0 3,7,0,4 3,4,2,1 3,2,0,5
Total max being 18
MAXIMUM NO OBTAINED BY ADDING ANY TWO OF THE GIVEN NO'S IS 13, POSSIBLE PRIME NO'S ARE 2,3,5,7,11,13 . CONSIDERING THE VERTICES CONTAINING 7(IT HAS TO CONTRIBUTE TO 3 EDGES),7+0=7,7+4=11,7+6=13. CONSIDERING THE VERTICES CONTAINING 6,6+7=13,6+1=7,6+5=11, CONSIDERING THE VERTICES CONTAINING 4,4+7=11,4+3=7,4+1=5. CONSIDERING THE VERTICES CONTAINING 5,5+6=11,5+2=7,5+0=5. THUS WE GET THE LOCATION OF ALL,THUS BEST PHASE PROVIDING MAXIMUM SUM IS ,7+6+5+0=18 0R7+6+4+1=18
Note that the maximum edge value is 6+7=13. Since there are only three prime numbers between 7 and 13, namely 7,11,and 13, 7 must share an edge with 0,4, and 6. Similarly, there are only three prime numbers between 6 and 13, thus 6 must share an edge with 1 7 and 5. Now consider the number that shares an edge with both 0 and 6 that isn't 7. This must be 5 since 0+1 isn't prime. Thus we have determined the relative positions of 0,5,6,7,1,and 4. The positions of 3 and 2 are fixed because the edges must be prime, and adding up at each face gives 18 as the answer
The first step is to choose a couple numbers and see what numbers it must must be added to in order to obtain a prime number.
Of the 8 numbers, you obtain 3 possible numbers for six of them so you are able to figure out which numbers are on the adjacent vertices through logic.(It isn't necessary to write all of these out. After obtaining a couple of these, you can begin deducing which numbers go where.)
0 : ( 2 , 3 , 5 , 7 ) , 1 : ( 2 , 4 , 5 ) , 2 : ( 0 , 1 , 3 , 5 ) , 3 : ( 0 , 2 , 4 )
4 : ( 1 , 3 , 7 ) , 5 : ( 0 , 2 , 6 ) , 6 : ( 1 , 5 , 7 ) , 7 : ( 0 , 4 , 6 )
In my solution, first I found that 4 must have 1, 3, and 7 on the adjacent vertices. I also found that 6 must have 1, 5, and 7 on the adjacent vertices so it must be on the same face as 1, 4, and 7. The remaining two numbers are 0 and 2. 0 cannot go with 1 since it doesn't form a prime number so 2 must go in that vertex leaving 0 to fill the final vertex.
WLOG, choose any vertex to be 1 . It is connected with 3 other vertices. They have to be 2 , 4 , 6 in some order. Assign the vertices in any order. Observe that the vertex diagonally opposite to 1 has to be 0 [since zero cannot be beside 4 , 6 ]. Since it is impossible to link 2 with zero in the current arrangement, it has to be linked with 3 , 5 , 7 . Trivially check how that can be done. It is also easy to show that this is a unique arrangement other rotation, reflection, etc.
always remember sum of even and odd will you odd(may be prime)but not sum of Odd-odd or even-even-thats the trick;because sum of even -even and sum of odd-odd is always even which defies the value to be Prime. start with 0 and match the other edge vertex with a prime ie..3 ,5,7 then match up with other vertices with the remaining values so that the resulting sum is a prime. never carry even-even or odd odd together.
the possible value are 5,0,6,7 or you may have 1,4,6,7
Step 1. Get the pairs of numbers such that the sum is prime. (0,1),(0,2), (1,2),(1,4),(2,3),(1,6),(2,5),(3,4),(0,7),(5,6),(4,7),(6,7),
The largest sums are 11 and 13. This must be included in the same face. This face has corners 6,7 and 4 with the corner opposite of 7 is 1. The sum of these numbers is 18.
A good way to start this problem is thinking what numbers could stay by side of zero. These numbers just could be the prime numbers 1,3,5,7. After, you have to realize that, between all numbers given, the only one which sumed with the numbers 6,4,2 results in a prime is the number 1. Thinking like this, the problem is resolved.
See the largest sum of a side is 18:
18=6+7+1+4
18+6+7+0+5
We will call a vertex by the number that it is labeled with.
Consider vertex 0 . The 3 adjoining vertices must be labeled with a prime number, so they must be 2 , 3 , 5 , or 7 . However, there could be no vertex that is a neighbor of both 2 and either of 3 , 5 or 7 , since one of the sums would be an even number greater than 2 , thus not prime. Hence 2 is not adjoining next to 0 . So the vertices adjoining 0 are 3 , 5 and 7 .
The only vertex that can be adjoining both 3 and 7 is 4 . The only vertex that can be adjoining both 3 and 5 is 2 . The only vertex that can be adjoining both 5 and 7 is 6 . The remaining vertex is 1 , which adjoins 2 , 4 and 6 , and we can check that the sums are prime.
Therefore the way to label the cube is unique (up to permutations of the cube).
It is easy to check that the maximum sum of the 4 numbers on a face is 7 + 6 + 5 + 0 = 7 + 6 + 4 + 1 = 1 8 .
The maximum of surface value is 18. There will be two such surfaces.
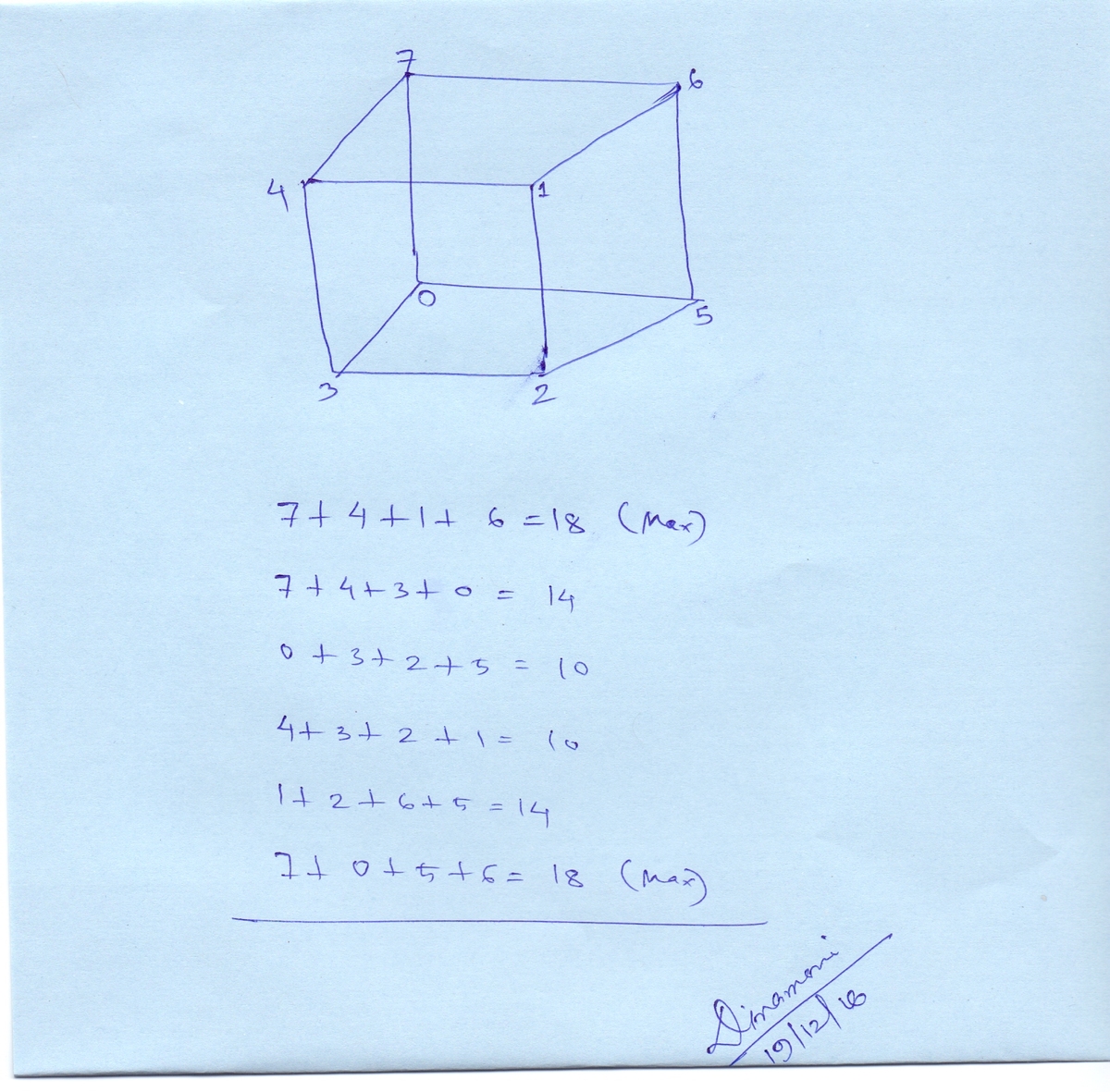
I drew a cube on paper and labelled the vertices in such a manner so that the sum of any two numbers on the same edge is a prime.
the face which has 7,2,4 and 5 as vertices has sum maximum.
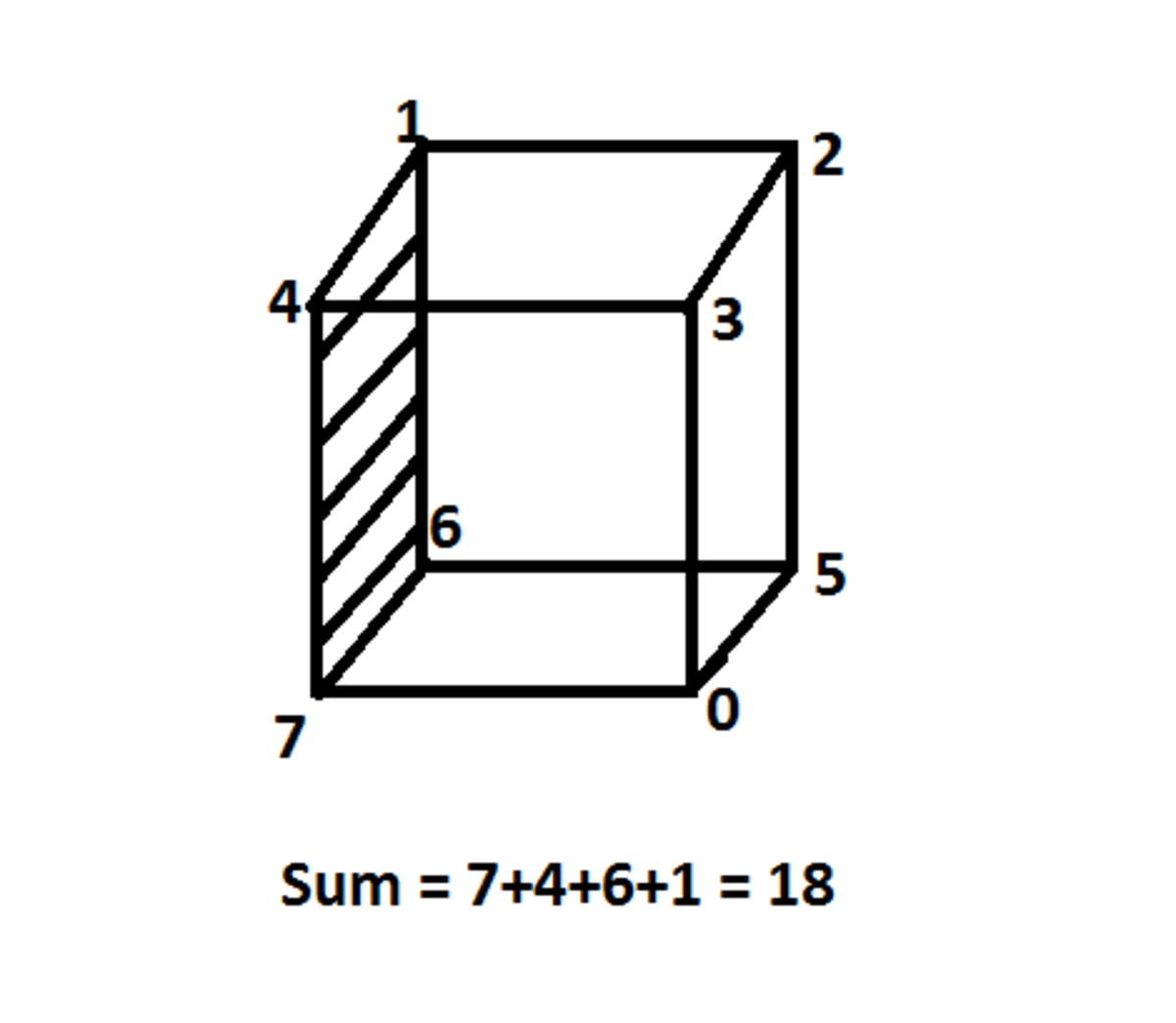
Since the vertices are numbered from 0 to 7, the maximum value an edge can have is 6+7=13. There are 6 prime numbers less than or equal to 13, and we can list all the options for getting edges to add up to those numbers:
2: 0+2
3: 0+3, 1+2
5: 0+5, 1+4, 2+3
7: 0+7, 1+6, 2+5, 3+4
11: 4+7, 5+6
13: 6+7
There are a total of 13 combinations, and we know there are 12 edges on a cube. So one combination will not be used. Also, each vertex on the cube is part of three different edges. So the numbers 0-7 should each appear in exactly 3 of the sums above. We can see that 0 and 2 appear four times, so the combination 0+2 must be the one that is not used.
Now to arrange the numbers on the vertices. There is only one arrangement (up to rotation and reflection) that uses the pairs in the sums. You can construct the arrangement by placing (for example) 0 at one vertex, and then placing the 3, 5, and 7 at the neighbouring vertices. Then there is a vertex that neighbours the 3 and 5, and (from the list of sums) we see that it must be the 2. You can proceed this way to label the remaining vertices.
Then it is a simple matter to compute the sum of the six faces, and choose the maximal one.