Maximum Ratio of Areas

Geometry Level 5

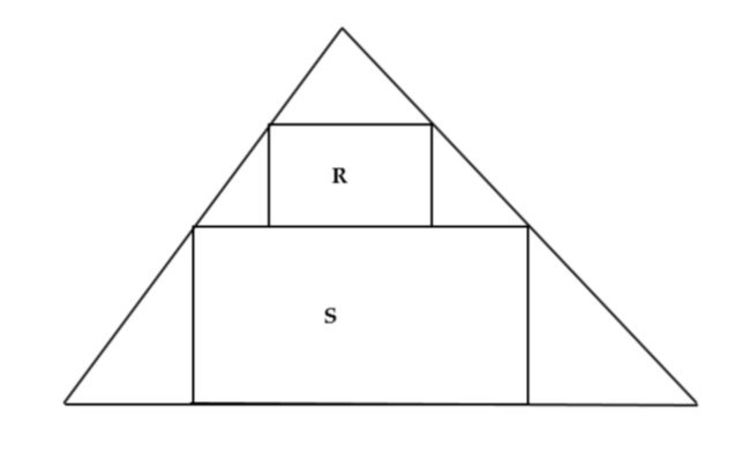Let $T$ be an acute-angled triangle, and $R$ , $S$ be rectangles inscribed in it as shown. If $A(x)$ denotes the area of the figure $x$ , the maximum value of $\displaystyle \dfrac{A(R)+A(S)}{A(T)}$ can be expressed as $\dfrac{P}{Q}$ , where $P,Q$ are coprime positive integers. Find the maximum possible area of a triangle with $P$ , $Q$ as two of it's sides.

The answer is 3.

2 solutions

Daren Wong
Dec 23, 2015

(I got the right-angled triangle by separating the acute-angled triangle into two and made both sides equal just to simplify things up). Let's inscribe a rectangle with sides x and y and we know that all that's left is a square with sides $\displaystyle \dfrac {x}{2}$ since the maximum area of a rectangle inscribed in an isosceles right-angled triangle is a square with its vertex touching the median of all three sides of the triangle. Thus, $\displaystyle \dfrac{A(R)+A(S)}{A(T)}$ equals $\displaystyle \dfrac {((\frac {x}{2})^2+xy)}{\frac {1}{2}}$ . Since its an isosceles right-angled triangle, $\displaystyle \tan \frac{\pi}{4} = \frac {y}{1-x}$ and so $y = 1-x$ . Substitute it back into the first equation and differentiate with respect to $\displaystyle x$ we get $\displaystyle x = \frac {2}{3}$ when $\displaystyle \dfrac {dy}{dx} = 0$ . By substituting the value of $x$ , we get the maximum value of $\displaystyle \dfrac{A(R)+A(S)}{A(T)} = \frac {2}{3}$ . Maximum value of triangle with sides of 2 and 3 is $\displaystyle \dfrac {2 \times 3}{2} = 3$

By "making" both sides equal and generating an isosceles triangle, this (Daren Wong's) solution only handles a special case (solves a simpler problem, which is only good for a conjecture, unless it is generalised later).

Zee Ell - 5 years, 5 months ago

Hi Zee EII, thank you very much for your opinion. Here, I would like to prove that the maximum ratio is the same be it a scalene triangle or an isosceles one. Let's say we set the two sides of the triangle as $\alpha$ and $\beta$ which are both constants and $\alpha \neq \beta$ , we get $\displaystyle \dfrac{A(R)+A(S)}{A(T)} = \frac {(\frac {\alpha - y}{2})(\frac {x}{2})+xy}{(\frac {\alpha \beta}{2})}$ . I separated the triangle into two smaller triangle with altitudes $x$ and $y$ . From here, we can set up another equation where the area of triangle equals the areas of the two smaller triangles combined, $\displaystyle \dfrac{\alpha \beta}{2} = \frac {x \alpha}{2} + \frac {y \beta}{2}$ . By substituting the second equation into the first equation, we get $\displaystyle \dfrac{A(R)+A(S)}{A(T)} = \frac {1}{2} +\frac {y}{\alpha} - \frac {3y^2}{2\alpha^2}$ . Differentiating it with respect to $\displaystyle y$ , we get $\displaystyle y = \frac {\alpha}{3}$ when $\displaystyle \dfrac {d(\frac{A(R)+A(S)}{A(T)})}{dy} = 0$ . Substituting it back into the equation, we get $\displaystyle \dfrac{A(R)+A(S)}{A(T)} = \frac {2}{3}$ where all the $\alpha$ cancels out. This shows that the maximum ratio will always be equal to $\displaystyle \dfrac {2}{3}$ for all types of acute-angled triangle.

Daren Wong - 5 years, 5 months ago

Thank you for your response. What I don't see here, is how you got the side length of the upper rectangle as $\frac {x}{2} and \frac {\alpha-y}{2}$ . We don't have an isosceles right triangle any more. Also, by differentiating your $\frac{1}{2}+\frac {y}{\alpha}-\frac {3y^2}{\alpha^2}$ expression with respect to y, and making the derivative equal to zero, we would get $y=\frac {\alpha}{6}$ instead of $y=\frac{\alpha}{3}$ ( $(3y^2)'=6y$ )

Zee Ell - 5 years, 5 months ago

@Zee Ell – Thank you for pointing that out, there was a typo. It should be $\displaystyle \dfrac {3y^2}{2\alpha^2}$ , I have edited it already in my previous comment. Regarding the side length of the upper rectangle, the rectangle inscribed in a triangle with the maximum area will be the one that has side lengths equals to half of the side lengths of the triangle. For example, if the triangle has side lengths of 3 and 4, the rectangle inscribed in it with the maximum area will have side lengths of 1.5 and 2.

Now, let's start off our proof by generating a triangle of sides $A$ and $B$ (where both are constants) and inside it is a rectangle with side lengths $a$ and $b$ . Like what I showed previously, by separating the triangle into two smaller triangle with altitudes $a$ and $b$ , we can set up an equation $\displaystyle \dfrac{AB}{2} = \frac {Ab}{2} + \frac {aB}{2}$ . The second equation would be the area of the rectangle, $\displaystyle Area = ab$ . By substitution of both equations and then differentiate Area with respect to $a$ or $b$ and then setting the derivative equals to zero, we get either $a = \frac{A}{2}$ or $b = \frac{B}{2}$ . This shows why the side length of the upper rectangle is therefore $\displaystyle \dfrac{x}{2}$ and $\displaystyle \dfrac{\alpha - y}{2}$ .

Daren Wong - 5 years, 5 months ago

@Daren Wong – Isn't your equation instead of $\frac{AB}{2}= \frac{Ab}{2}+ \frac{aB}{2}$ rather $\frac{AB}{2}= \frac{Ab}{2}+ \frac{aB}{2}+ab$ ? I would like to see your steps in more detail (especially the "substitution of both equations and then differentiate the Area with respect to a or b" part).

Zee Ell - 5 years, 5 months ago

@Zee Ell –

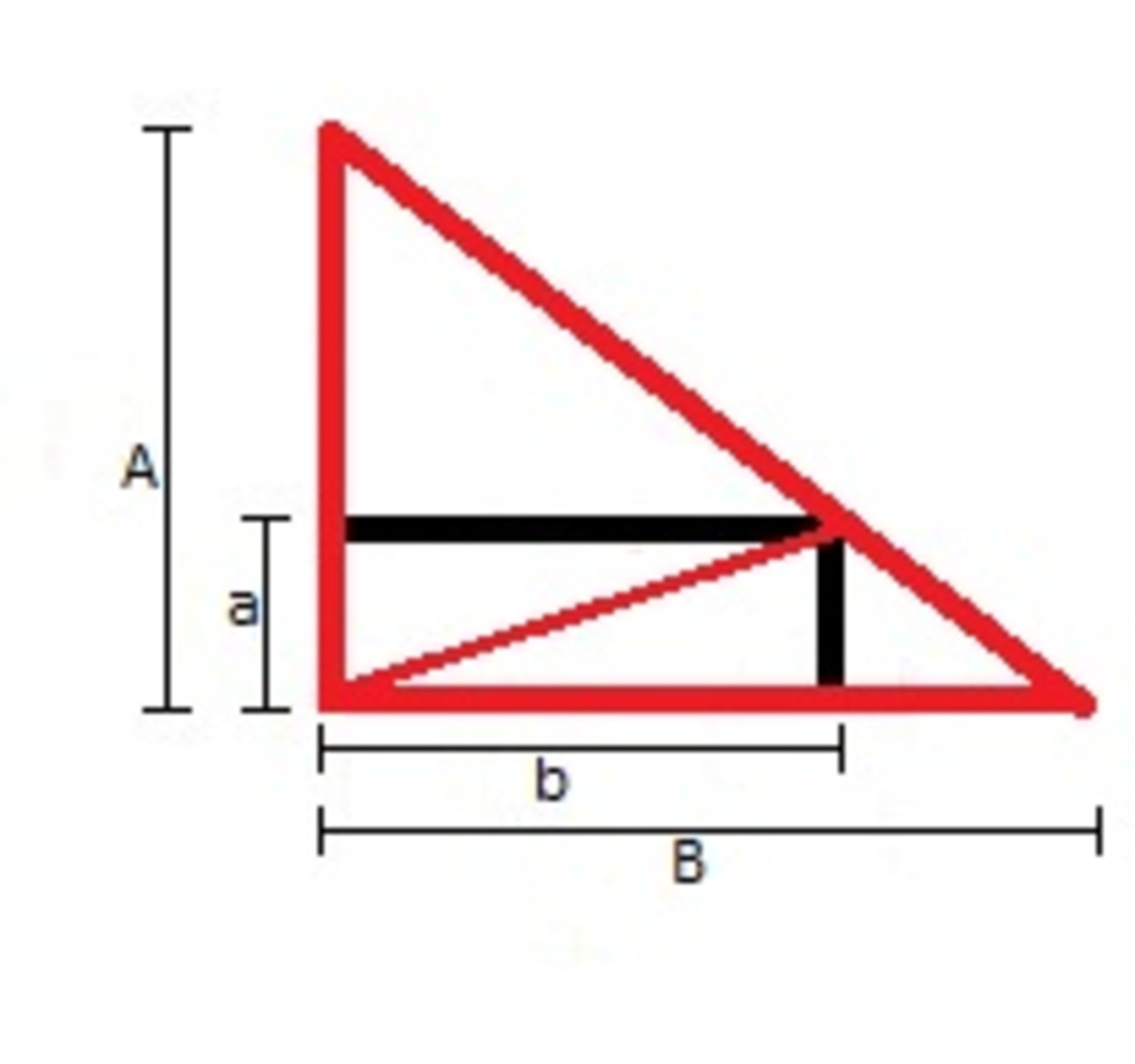
From this diagram, it is very clear that the equation is really $\frac{AB}{2} = \frac {Ab}{2} + \frac {aB}{2}$ and not $\frac{AB}{2}= \frac{Ab}{2}+ \frac{aB}{2}+ab$ . This equation is derived from the area of the big triangle equals to the sum of the areas of two smaller triangles with altitudes $a$ and $b$ . By expressing the equation for $a$ in terms of $b, A, B$ , we get $a = \frac {A}{B}(B-b)$ . By substituting this into our area equation, we get $Area = b( \frac {A}{B}(B-b))$ . Expand it and $Area = Ab - \frac {Ab^2}{B}$ . Differentiate the entire equation with respect to $b$ . $\frac {d(Area)}{d(b)} = A - \frac {2Ab}{B}$ . By setting the derivative equals to zero, we can cancel out the $A$ leaving $b = \frac {B}{2}$

Daren Wong - 5 years, 5 months ago

@Daren Wong – Thanks for the diagram and the additional explanation, which made things clearer. As far as I can see, you really have another correct solution now.

Zee Ell - 5 years, 5 months ago

i did a lot of assumptions

Akash singh - 5 years, 3 months ago

Zee Ell
Dec 20, 2015

Draw the altitude of the triangle which is perpendicular to the common side AF the triangle and rectangle R!

This altitude splits T triangle into two right angled triangles, T1 and T2. Each of these two new triangles contain three smaller right triangles (T11, T12, T13 and T21, T22, T23 respectively), which are similar to them. The scale factor is the ratio of the altitudes (sides, we use the same altitude for T, T1 and T2, which is the same as the sum of the altitudes of the 3 small triangles), the areas have a ratio which is the square of the scale factor. (Alternatively, we can also combine the top, the middle and the bottom pairs of small triangles into 3 bigger ones, which are similar to the original triangle T.)

As our original triangle T contains only R, S and these 3+3=6 triangles, therefore the fraction $M=\frac{A(R)+A(S)}{A(T)}$ asked will be maximal, when the ratio between the total area of the small triangles and the area of T, that is $N=\frac{A(T11)+...+A(T23)}{A(T)}=1-M$ is minimal.

Due to the similarity, area factors and the AM<=QM (the inequality regarding the arithmetic and the quadratic mean), N is minimal when equality holds, which happens when the altitudes of the small triangles split the altitude of T into three equal parts. This gives us scale factors of $\frac {1}{3}$ and area factors of $(\frac{1}{3})^2=\frac{1}{9}$ .

Therefore,

$N=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{1}{3}$

and $M=1 - N =\frac {2}{3} = \frac {P}{Q}$ , so P=2 and Q=3.

The maximum area of a triangle with sides 2 and 3 is

$\frac{2×3×sin90°}{2} = 3$ ,

as the sin(x) function has its maximum at 90°.

Maximum Ratio of Areas

The answer is 3.

2 solutions

0 pending reports