Measure of an Interior Angle
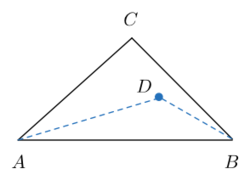
Triangle A B C has A C = B C and ∠ A C B = 9 6 ∘ .
D is a point in A B C such that ∠ D A B = 1 8 ∘ and ∠ D B A = 3 0 ∘ .
What is the measure (in degrees) of ∠ A C D ?
The answer is 78.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
the answer is 18 for ACD, in the case of BCD is 78
Isn't sine only for right triangles?
x-y=24 (sin (48+x))/z = (sen(132-x))/z x= 42 y=18 =ACD 96-18= 78=BCD
I have a pure geometry solution.
It is apparent that CAD=24 and CBD =12. Take bisector of CAD and extend BD to let it meet at P.
Now CAP =12 and CBP = 12 . So AP=PB( PAB = PBA = 30 ^).
So P is on perpendicular bisector of AB and C is on perpendicular bisector of AB. So join CP. => ACP =96/2=48.
In triangle PAB , PA=PB => PAB= PBA=30 => APB=180-60=120.
In triangle PAD PAD=12, APD=120 =>PDA=48.
So triangle ACP and triangle ADP are congruent
(PCA=PDA=48,PAD=PAC=12,APC=APD=120 and SIDE AP is common)
APC <--->APD is congruent so AC=AD and So angles ACD=ADC= (180-24)/2=78.
Arpan Shah It is: APC <--->APD is congruent so AC=AD and So angles ACD=ADC= (180-24)/2=78.
Very nice indeed. How did you think of it?
Log in to reply
Well I am an ardent lover of geometry.......
Log in to reply
Yay! There are many more amazing problems like this to work on :)
you are too smart
Please see last sentence
ACD=ADC= (180-24)/2=78
Not 12 it's 24!
Applying the cosine rule to ∠ A C B with A C = B C , we have A B = A C 2 ( 1 − cos 9 6 ∘ ) = 2 ( sin 4 8 ∘ ) A C cos 9 6 ∘ = 1 − 2 sin 2 4 8
We also have that sin ∠ A D B = sin ( 1 8 0 ∘ − 1 8 ∘ − 3 0 ∘ ) = sin 1 3 2 ∘ = sin 4 8 ∘ . Thus applying the sine rule to triangle A D B , and substituting for A B , we have D A = sin 4 8 ∘ A B × sin 3 0 ∘ = A C . Thus D A C is an isosceles triangle.
Since triangle A C B is isosceles, we have ∠ C A B = 2 1 ( 1 8 0 ∘ − 9 6 ∘ ) = 4 2 ∘ . Thus ∠ C A D = 4 2 ∘ − 1 8 ∘ = 2 4 ∘ . Now since A C D is isosceles, we have ∠ A C D = 2 1 ( 1 8 0 ∘ − 2 4 ∘ ) = 7 8 ∘ .
lol i just drew the triangle and then i just divided the angles CAB into 2 parts.thus the angle to ab was about 18 degrees,then i divided the angle ABC into 2 parts so the angle from the line ab is now degrees.i drew a straight line through both the angles 18 degrees and 30 degrees and at one point the both lines met,the point the both lines met was the point D.After measuring with a protractor the value i git was something like 76 degrees ,the answer is 78 degrees and the reason i got 76 is due to the fact i used a whiteboard and the lines were think,so i assume my way of doing it is correct as i git an answer in that range and i wudv gotten 78 if i done it on paper.
Log in to reply
Problems like this are meant to be done without accurate construction. Yes, drawing an accurate diagram is one way to determine the numerical answer, but the purpose is to demonstrate the thought process to arrive at the answer in a logical manner.
This is cheating!..if you use trigonometry!
Log in to reply
How is using trigonometry cheating?
Log in to reply
Well have been struggling to solve the problem with out any use of trigonometry,if you use trigonometry it would become ordinary maths question,I used Autocad to solve it!
Log in to reply
@Addisu Hackerman – This is an "Euclidean Geometry" problem that is common in competitions. You can use any method to prove the calculations.
I would argue that reproducing the image through accurate diagrams would be more of "cheating", as that provides no proof for why the angle is exactly 78, instead of (say) 78.01.
Constructions:- Let A D ∩ C B = E . Draw the angle bisector of ∠ B A D to meet B D produced at I . Join C I and E I as well. It's easy to conclude via simple angle chasings that ∠ E A I = ∠ E B I = 1 2 ∘ and ∠ A E C = 6 0 ∘ . Now in quadrilateral A I E B , ∠ E A I = ∠ E B I = 1 2 ∘ , therefore quad. A I E B is cyclic. ∠ D I E = ∠ D A B = 1 8 ∘ − − − − e q n 1 Also, ∠ I E A = ∠ I B A = 3 0 ∘ . But since, ∠ A E C = 6 0 ∘ and ∠ I E A = 3 0 ∘ therefore, E I is the bisector of ∠ A E C = > I is the incenter. Therefore, A I bisects ∠ A = > ∠ I A E = 4 8 ∘ . But, ∠ I D E = ∠ A D B = 1 3 2 ∘ . Therefore, ∠ I A E + ∠ E D I = 1 8 0 ∘ = > C I D E is cyclic. = > ∠ D C E = ∠ D I E = 1 8 ∘ [Using e q n 1 ] = > ∠ A C D = 7 8 ∘ .
Just K . I . P . K . I . G
ΔABC is a isosceles triangle, solve for angle CAB
CAB = (180-96)/2 = 42 , ADB=180-18-30=132 and CAD=42-18=24
Assume AC and CB equal to 1 and solve for AB by sine rule. Use AB to solve for DA by sine rule. Then we found that DA=AC, ΔACD is isosceles triangle, therefore ACD=(180-24)/2 = 78