Mechanics |07-06-2021|
A uniform rod of mass
m
and length
l
is hanging vertically from the pivot O.A horizontal force
F
acts at the lower end of the rod .
If
F
always remains horizontal then maximum angular displacement of rod is
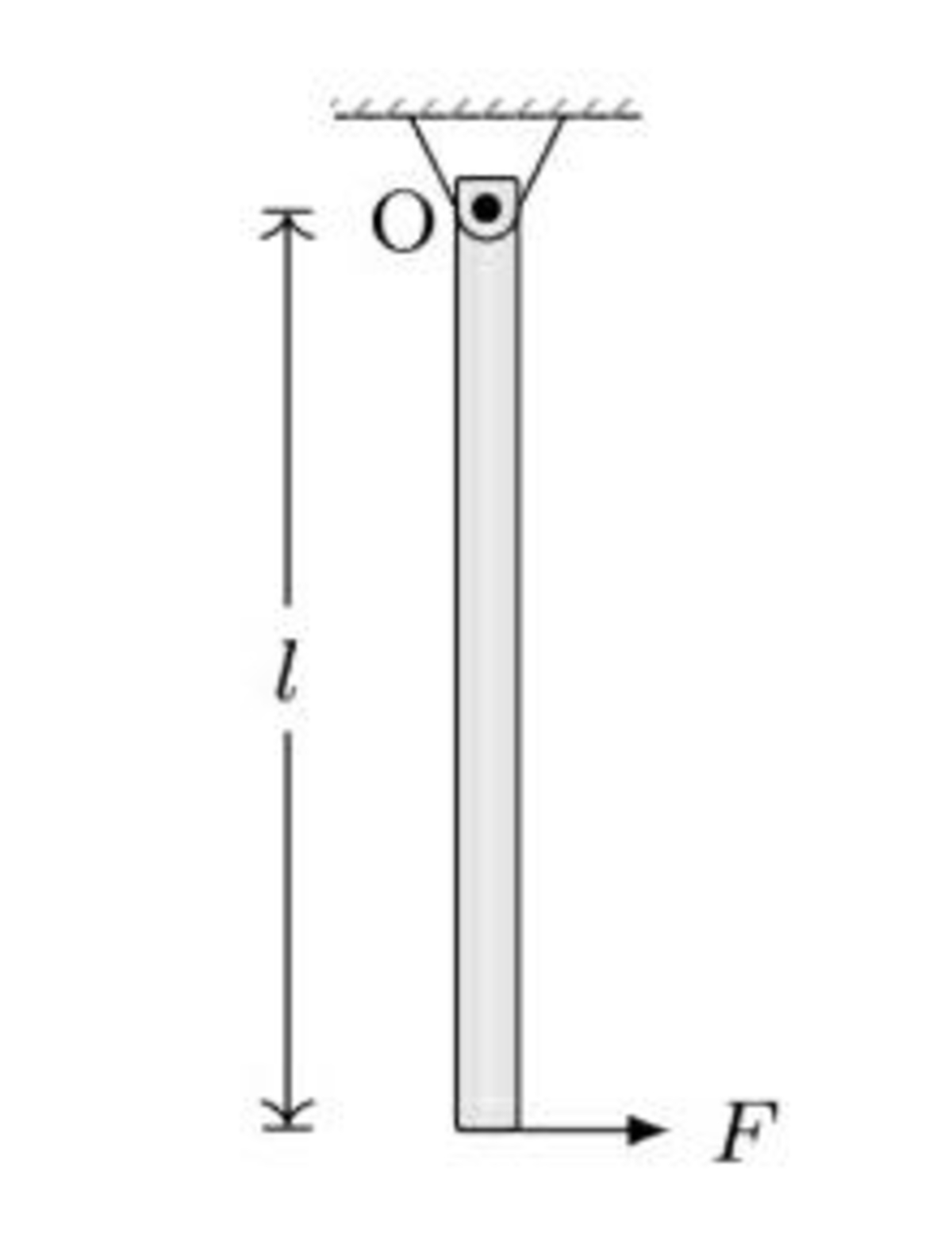 .
.
Answer comes in the form of
α
tan
−
1
(
m
g
β
F
)
.
Type your answer as
α
+
β
+
γ
.
Note .
1)
If removing community section is a right decision then
γ
=
1
.
2)
If removing community section is a wrong decision then
γ
=
2
3)
g
is gravitational force which is acting in downward direction.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath
Thanks for the solution.
By the way why your country oscillates between Netherlands and USA?
@Karan Chatrath
Did you got the answer from staff about previous problems ?
Share with me .
Can we also use conservation of energy for this? I got the answer in like 2 steps from that but not really sure if that's the right approach
Log in to reply
Share the approach
Energy conservation is a faster way of solving. Essentially, the difference between the final and initial total energies of the system is equal to the work done by the force. This gives us:
E f − E i = W f ( 2 I θ ˙ 2 − 2 m g L cos θ ) − ( − 2 m g L ) = F L sin θ
Since the final KE must be zero:
⟹ ( − 2 m g L cos θ ) − ( − 2 m g L ) = F L sin θ
Which leads to the answer.
Log in to reply
@Karan Chatrath After Brilliant where will you upload your solutions and problems ?
Log in to reply
@Talulah Riley – Don't yet know a way. When I do, I'll let you know. Also, I have not heard back from Brilliant support staff.
Yup, did pretty much this. Thanks. Btw just learned about Brilliant about a month back, so is this the first time they're disabling the community? And is this permanent?
Log in to reply
@Deepankur Jain
–
@Deepankur Jain
Yes ,this is the first time they are doing this nonsense thing .
And they said they can probably again install a community section.they are unsure about it.
Log in to reply
@Talulah Riley – Oh ok. But this was a good platform for discussion, it's unfortunate they're taking this decision :(
At a general time t let the angle the rod makes with the vertical be θ . At this instant, computing the net torque about the point O leads to the equation:
( 3 m L 2 ) θ ¨ = F L cos θ − 2 m g L sin θ ⟹ θ ¨ = m L 3 F cos θ − 2 L 3 g sin θ
The initial conditions are: θ ( 0 ) = θ ˙ ( 0 ) = 0 . Since the rod hangs vertically, it is initially assumed to be at rest.
Now, applying the following manipulation:
d t 2 d 2 θ = d θ d θ ˙ d t d θ = θ ˙ d θ d θ ˙
Plugging this into the equation of motion:
θ ¨ = θ ˙ d θ d θ ˙ = m L 3 F cos θ − 2 L 3 g sin θ ]
Separating variables and integrating:
∫ θ ˙ d θ ˙ = ∫ ( m L 3 F cos θ − 2 L 3 g sin θ ) d θ ⟹ 2 θ ˙ 2 = m L 3 F sin θ + 2 L 3 g cos θ + c
Plugging in initial conditions and solving for c leads to the final relation:
2 θ ˙ 2 = m L 3 F sin θ − 2 L 3 g ( 1 − cos θ )
The maximum angular displacement is achieved when the rod again comes to rest. This means θ ˙ = 0 . This means:
2 L 3 g ( 1 − cos θ ) = m L 3 F sin θ 2 L 3 g 2 sin 2 ( 2 θ ) = m L 3 F ( 2 sin ( 2 θ ) cos ( 2 θ ) ) ⟹ tan ( 2 θ ) = m g 2 F θ m a x = 2 arctan ( m g 2 F )
⟹ α = β = 2