Men area

We have a regular hexagon with area 240. Let us denote the length of one side as $s$ .

Now, examining our hexagon, because M is a midpoint, $MD = \frac{s \sqrt{3}}{2}$ . Using the Pythagorean Theorem we can find $ME = \frac{s \sqrt{7}}{2}$ .

Furthermore, $NF = \frac{s}{2}$ (because N is a midpoint), and using the Law of Cosines and the fact that internal angles of a regular hexagon are 120, $NE = \frac{s \sqrt{7}}{2}$ .

Now, upon further examination, triangle $BNM$ is isosceles with base $BM$ . Thus, $BN \cong MN$ , and because $BN \cong NE = \frac{s \sqrt{7}}{2}$ , by the transitive property, $NM = \frac{s \sqrt{7}}{2}$ .

We have an equilateral triangle, so $Area = \frac{\sqrt{3}}{4}s^{2} \frac{7}{2}$ .

Using the fact that the area of the hexagon is $240$ , we can determine that $s^{2} = \frac{160}{\sqrt{3}}$

Plugging in, the area and answer is $70$ .

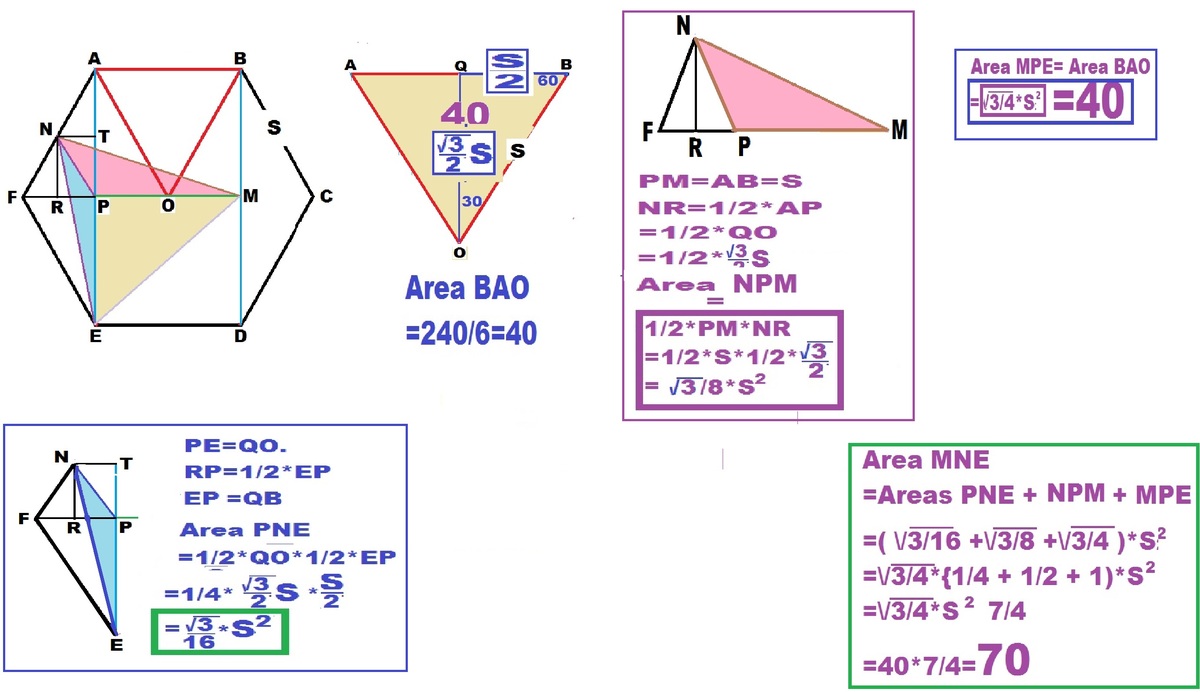
Let the side length of the hexagon be $s.$ Then the area of the hexagon is $\dfrac{3s^2\sqrt3}{2} = 240,$ which can be seen by dividing the hexagon up into six equilateral triangles. We will compute the area of $\triangle MEN$ by first finding the area of $FEMN$ and then subtracting the area of $\triangle FEN.$

Let $AE$ and $FM$ intersect at $P.$ Then $PM = s$ and $FP = s/2$ (from the properties of $30-60-90$ triangles), so $FM = \frac{3s}{2}.$ Now let $X$ be the foot of the perpendicular from $N$ to $FM.$ $\triangle FNX$ is also a $30-60-90$ triangle, so $NX = \dfrac{s\sqrt3}{4}.$ Therefore, the area of $\triangle FNM$ is $\frac{1}{2} \cdot \frac{3s}{2} \cdot \frac{s\sqrt3}{4} = \frac{3s^2\sqrt3}{16} = \frac{1}{8}\left(\frac{3s^2\sqrt3}{2}\right) = \dfrac{1}{8}(240) = 30.$

---

Let $Y$ be the foot of the perpendicular from $E$ to $FM.$ Then $YE = \dfrac{s\sqrt3}{2},$ which is twice $XN.$ Therefore, the area of $\triangle FEM$ is twice the area of $\triangle FNM,$ or $2(30) = 60.$

Thus, the area of $FENM$ is $30 + 60 = 90.$

Now we find the area of $\triangle FEN,$ using the sine area formula. We have $FN = s/2,$ $FE = s,$ and $\angle EFN = 120^{\circ},$ so the area of triangle $FEN$ is $\frac{1}{2} \cdot \frac{s}{2} \cdot s \cdot \sin 120^{\circ} = \dfrac{s^2\sqrt{3}}{8} = \dfrac{1}{12}(240) = 20.$

Finally, the area of $\triangle MEN$ is $90 - 20 = \boxed{70}.$

Let the length $AB=2x$ Apply Pythagoras' Theorem to find that $MD=\sqrt{3}x, ME=\sqrt{7}x$ Use the cosine rule to find that $EN=\sqrt{7}x$

Draw a line parallel to AB through N. Let this line meet BD at P. Then we have $NP=\frac{5}{2}x, PM=\frac{\sqrt{3}}{2}x,NM=\sqrt{7}x$

So MEN is an equilateral triangle with side length $\sqrt{7}x$ .

The ratio of areas of similar shapes is the square of the ratio of sides. So we have Area MEN $=(\frac{\sqrt{7}}{2})^2 \times 40=70$

Let mid point of AE be O(0,0). Let each side of hexagon be 'a'.

So we have the following coordinates:

$A(0,\frac{\sqrt{3}a}{2})$

$B(a,\frac{\sqrt{3}a}{2})$

$C(\frac{3a}{2},0)$

$D(a,\frac{-\sqrt{3}a}{2})$

$E(0,\frac{-\sqrt{3}a}{2})$

$F(\frac{-a}{2},0)$

Hence, we have,

$M(a,0)$ and $N(\frac{-a}{4},\frac{\sqrt{3}a}{4})$

Now we can use distance formula to find each of $NE=NM=EM = p = \sqrt{\frac{7a^{2}}{4}}$

Which means $\triangle NEM$ is equilateral and its area is $\frac{\sqrt{3}p^{2}}{4} = \frac{7\sqrt{3}a^{2}}{16}$

Also, area of hexagon is $A = 2*\frac{1}{2}*(a+2a)*\frac{\sqrt{3}a}{2} = \frac{3\sqrt{3}a^{2}}{2}$

Area of $\triangle NEM$ is $A*\frac{7}{3}*\frac{1}{8} = 70$

.