Meta-Medians
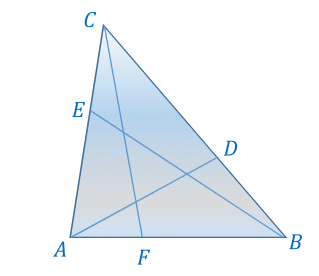
In a triangle A B C the points D , E , F are located on sides A B , B C , and C A respectives so that A B A F = B C B D = C A C E = 3 1 . Find the value of the ratio A B 2 + B C 2 + C A 2 A D 2 + B E 2 + C F 2
If the result is in the form b a , where a and b are coprime positive integers, report a + b .
Inspiration: Triangle Centroid by Worranat Pakornrat
Note: Drawing is not to scale.
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If we apply the Stewart's theorem, then the angle becomes redundant, and the calculations are straight forward as well.
Log in to reply
The angle is and was redundant from the start. It was sneaked in to discourage the shortcut of going straight to an equilateral triangle without ever considering the general problem. Unfortunately it also misleads in other ways, as well as detracts from any aesthetic appeal. You can't have it all, I guess.
Log in to reply
Could you add that as a comment at the top of the solution? It's great that you're aware you introduced extraneous information :)
Log in to reply
@Calvin Lin – On careful consideration, I have decided to remove the extraneous information. I think the problem is more elegant this way.
Yeah, to be honest I didn't go through your solution, since it was long. Given that you used cosine rule, and a proof for Stewart's uses cosine rule, it is more or less the same.
Stewart's theorem, applied to this situation, would be:
3 a b 2 + 3 2 a c 2 = 2 ( α 2 + 9 2 a 2 )
It is not obvious to me how this contributes in any straigh-forward way.
Log in to reply
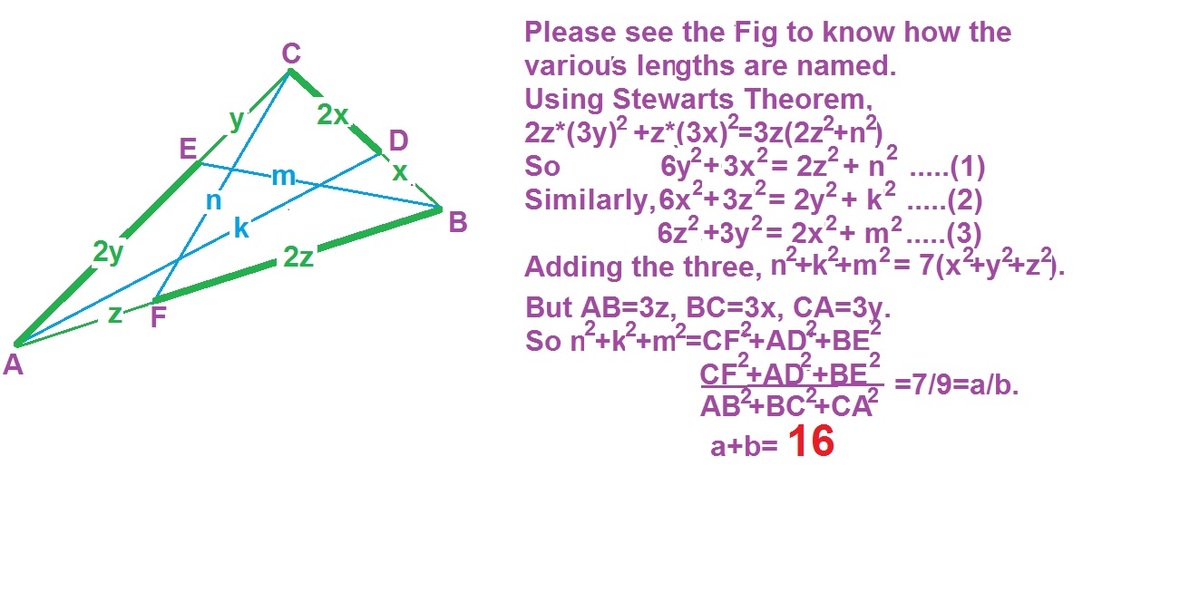
If we sum the three equations for AD^2, BE^2, CF^2 then the sum can be simplified to 7/9(a^2 + b^2 + c^2).
Let's introduce a = B C , b = C A , c = A B , α = C F , β = A D , γ = B E . We want to find
a 2 + b 2 + c 2 α 2 + β 2 + γ 2
Law of cosines applied three times to △ A B C :
a 2 = b 2 + c 2 − 2 b c × c o s A
b 2 = a 2 + c 2 − 2 a c × c o s B
c 2 = b 2 + a 2 − 2 a b × c o s C
The three lines added together and the result simplified:
a 2 + b 2 + c 2 = 2 ( a 2 + b 2 + c 2 ) − ( 2 b c × c o s A + 2 a c × c o s B + 2 a b × c o s C )
a 2 + b 2 + c 2 = ( 2 b c × c o s A + 2 a c × c o s B + 2 a b × c o s C )
Law of cosines used for the not-quite-medians:
α 2 = b 2 + ( 3 c ) 2 − 2 b 3 c × c o s A
β 2 = c 2 + ( 3 a ) 2 − 2 c 3 a × c o s B
γ 2 = a 2 + ( 3 b ) 2 − 2 a 3 b × c o s C
There three lines added and simplified:
α 2 + β 2 + γ 2 = 9 1 0 ( a 2 + b 2 + c 2 ) − 3 1 ( 2 b c × c o s A + 2 a c × c o s B + 2 a b × c o s C )
The last expression replaced with the result from the first three lines:
α 2 + β 2 + γ 2 = 9 1 0 ( a 2 + b 2 + c 2 ) − 3 1 ( a 2 + b 2 + c 2 ) = 9 7 ( a 2 + b 2 + c 2 )