Millions of years passed still the same unknown $x$

Calculus Level 2

$\large f_n(x) = \Large \underbrace{x^{x^{ x^{x^{\cdot^{\cdot^{\cdot ^x}}}}}}}_{\text{ number of } x \text{'s = } n}$

What is $\displaystyle \lim_{x\to0^+} \big(f_{2016} (x) + f_{2017} (x) + f_{2018}(x)\big)?$

0 1 2 3

7 solutions

Rishabh Bhardwaj
Apr 22, 2018

Start: As lim ( $x \rightarrow 0)\ x^x = 1$ ,

[let me know if proof needed, it's simple: 1) Take log both sides; 2) Apply L'Hospital's Rule; and 3) Take anti-log.]

Approach:

Now,

$1)$ lim ( $x \rightarrow 0)\ x^{x^x} = 0$ ,

[It's just lim ( $x \rightarrow 0$ ) $x$ raised to the power lim ( $x \rightarrow 0$ ) $x^x$ , i.e., lim ( $x \rightarrow 0)\ x^1 = 0$ ]

$2)$ lim ( $x \rightarrow 0)\ x^{x^{x^x}} = 1$ ,

[It's just lim ( $x \rightarrow 0$ ) $x$ raised to the power lim ( $x \rightarrow 0$ ) $x^{x^x}$ , i.e., lim ( $x \rightarrow 0)\ x^x = 1$ , using-1]

Conclusion:

Similarly, for any power of $x$ , we can determine the limit depending on the number of $x$ in the equation. For even $n$ ( $n$ is the number of $x$ in $f$ ), the limit will always be 1; and for odd $n$ , it will be $0$ .

Answer:

1( $n$ = 2016) + 0( $n$ = 2017) + 1( $n$ =2018) = 2

[Note: Each limit is $x$ tending to $0^{+}$ .]

Step 2 under "approach" doesn't look right. I'll be able to elaborate later if necessary, but it looks like you're doing the 0^0=1 error.

Brian Moehring - 3 years, 1 month ago

Not neccesary, since lim x^x^x =lim x^1 = lim x. That means lim x^x^x^x = lim x^x, not only x^0. But it probably should be in the proof.

Leszek Czajka - 3 years, 1 month ago

I should clarify I meant the justification for (2), not that statement (2) itself is incorrect.

Brian Moehring - 3 years, 1 month ago

Thanks Leszek, Brian, I have included your corrections.

Rishabh Bhardwaj - 3 years, 1 month ago

In step 1 why you took 0^1 not 1^0?

kalpesh kotwal - 3 years, 1 month ago

Are you confused in x^x^x?...It is x^(x^x) not (x^x)^x, hence, it should be x^1 not 1^x. :)

Rishabh Bhardwaj - 3 years, 1 month ago

Weird, I did not get that result. Let me elaborate on what I got.

If not mistaken, ln(fn(x))=x^(n-1) ln(x) = ln(x) / x^(1-n). For n>1, we can find limit of this expression using l'Hospital rule, i.e. numerator d ln(x)/dx = 1/x and denominator d x^(1-n)/dx = (1-n) x^(-n). Thus, we get (1/x) / ((1-n) x^(-n)) = -x^(n-1) / (n-1). The limit is 0. Ln-inverse gives limit of 1 for n>1. I graphed fn(x) for different values of n in matlab and got that fn(x) approaches 1 from below as x goes to zero from above for n>1. For n=1, the limit is 0, of course.

By ln-inverting the l'Hospital intermediate result "-x^(n-1) / (n-1)" we get exp(-x^(n-1) / (n-1)) which approximates as 1 - x^(n-1) / (n-1) for small x. In Matlab, this approximation shows same convergence rate to 1 as fn(x) itself.

If wrong, can you spot the mistake I made and detail why even and odd n would give different results? Thank you.

Pierre Carrette - 3 years, 1 month ago

Hi Pierre! Can you please tell me how did you get x^(n-1) in the first line itself? For instance, 2^2^2 = 2^(2^(2)) = 2^4 = 16. I guess you are writing 2^2^2 = 2^2? and then taking log both sides.

Rishabh Bhardwaj - 3 years, 1 month ago

No, just got it that a^b^c = a^(b^c) instead of (a^b)^c=a^(bc). My mistake ... the quiz then gets very simple. Note that Matlab is making same mistake in ^ prioritization.

Pierre Carrette - 3 years, 1 month ago

@Pierre Carrette – Oh... There is some rule that every language follows; better to incorporate brackets ourselves.

Rishabh Bhardwaj - 3 years, 1 month ago

Got it! Just did wrong ^ prioritization ... bugger

Pierre Carrette - 3 years, 1 month ago

Joshua Lowrance
Apr 5, 2018

The limit of 0^0 from the positive side is 1. However, the limit of 0^0^0 from the positive side is 0^1 or 0. The same applies for any large number of 0's. If there is an even number of 0's, the answer will be 1. If there is an odd number of 0's, the answer will be 0. Therefore, the answer is 1 + 0 + 1 = 2

John Ross
Apr 22, 2018

The limit of a tower with an odd number of x's is 0. We will show this by induction. The base case of one x is obvious. We can see that $\Large f_{2n+1}(x) = x^{x^{f_{2n-1}(x)}}$ The limit of this function will be 0 as well. The limit of an even number of x's is 1. We can see that $\Large f_{2n}(x) = x^{f_{2n-1}(x)}$ The limit of this function will be 1. The question is asking for the limit of 2 evens plus 1 odd, so the answer is 2.

Jeffrey H.
Apr 22, 2018

Cheap solution without words

Jacob Gartner
Apr 29, 2018

That is so f**king easy

Haoran Wang
Apr 29, 2018

infact, in f∞(x), x can use in[1/e^e, e^1/e]. because if x approach 0, fn(x) will jump between 1 and 0.when n=1, that lim is 0, and when n=2 that is 1, and when n=3, is 0 again. so when n is odd, that is 0, when n is even, that is 1. so question is 1(2016 is even)+0(2017 is odd)+1(2018 is even)=2.

Viktor Zdravkov
Apr 28, 2018

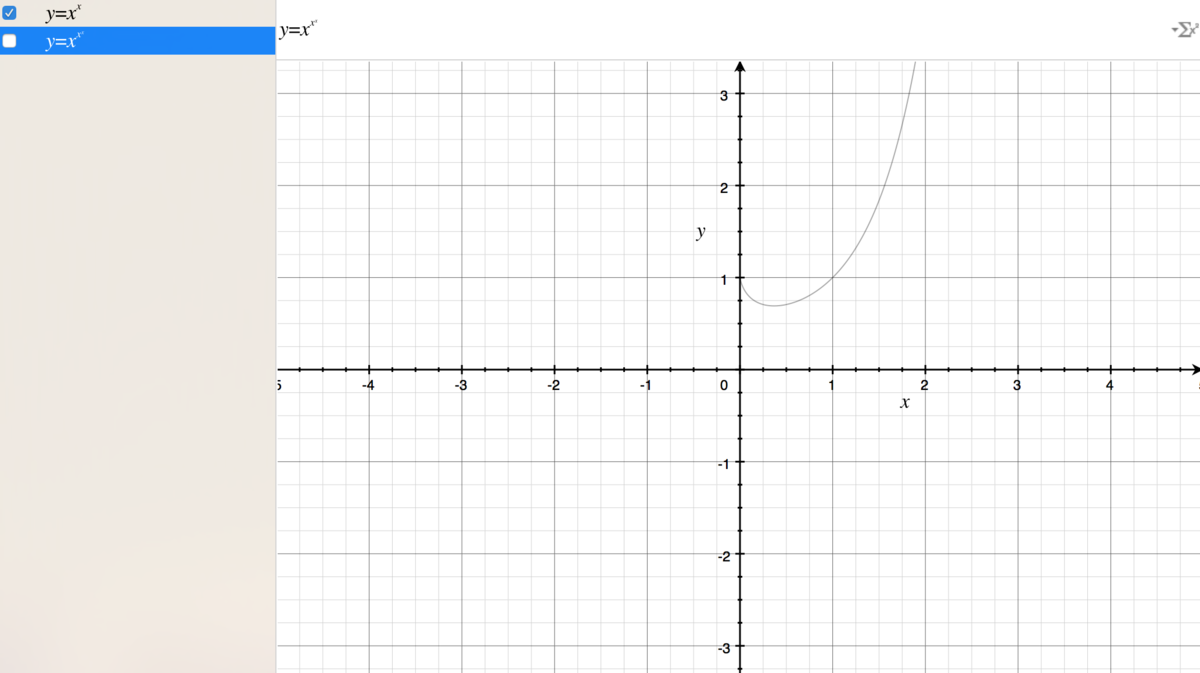
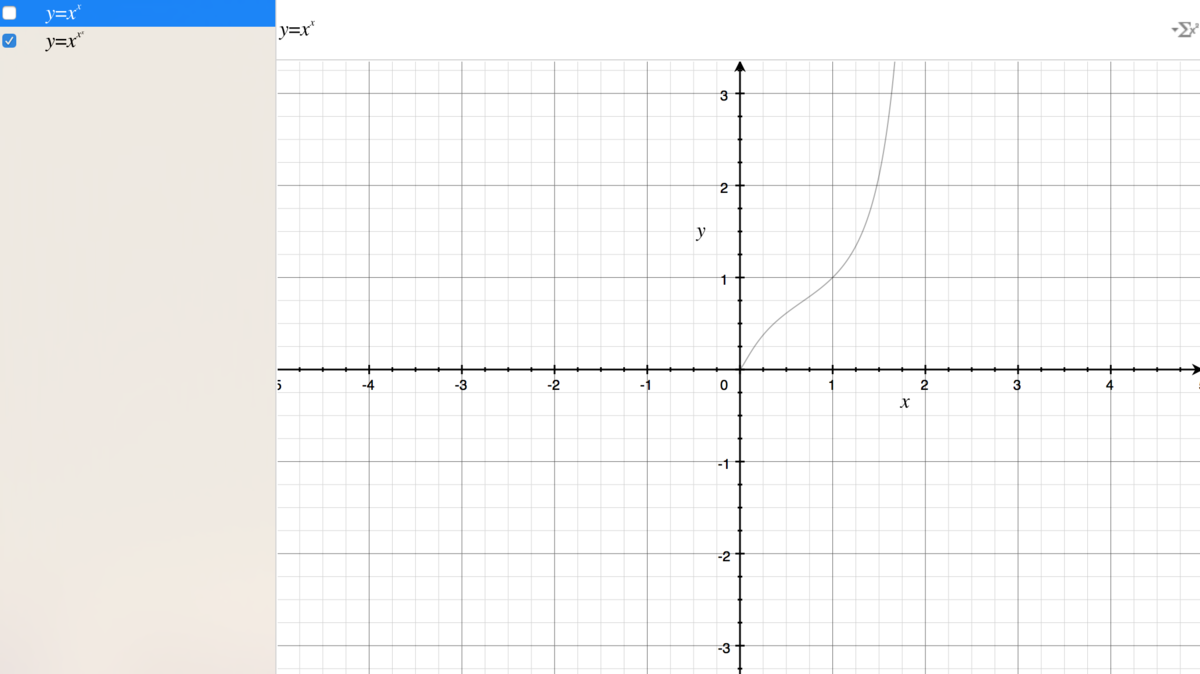
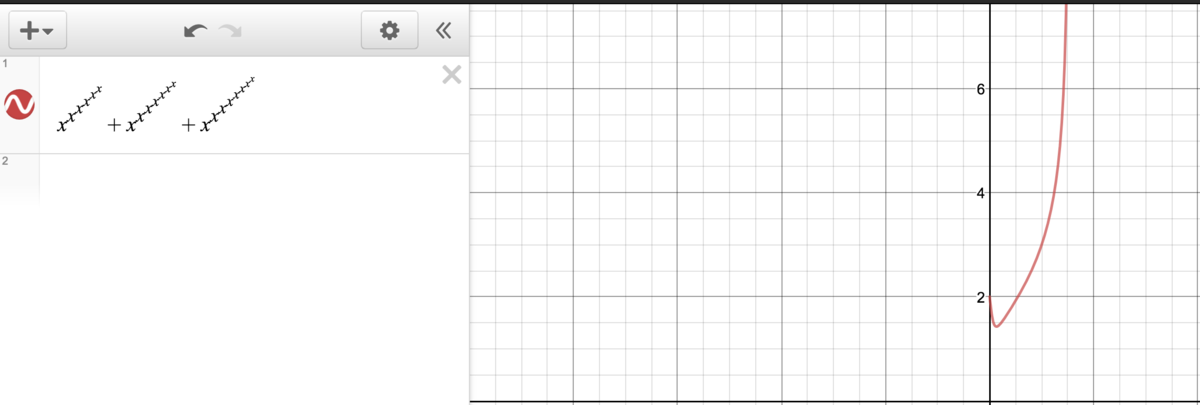
Plot x^x function.
Check Y behavior when adding exp(x).
Notice function is pair sensitive when approaching to 0.
Solve: 1+ 0 + 1 = 2

Millions of years passed still the same unknown x x x

7 solutions

0 pending reports

Millions of years passed still the same unknown $x$