Minimising H I
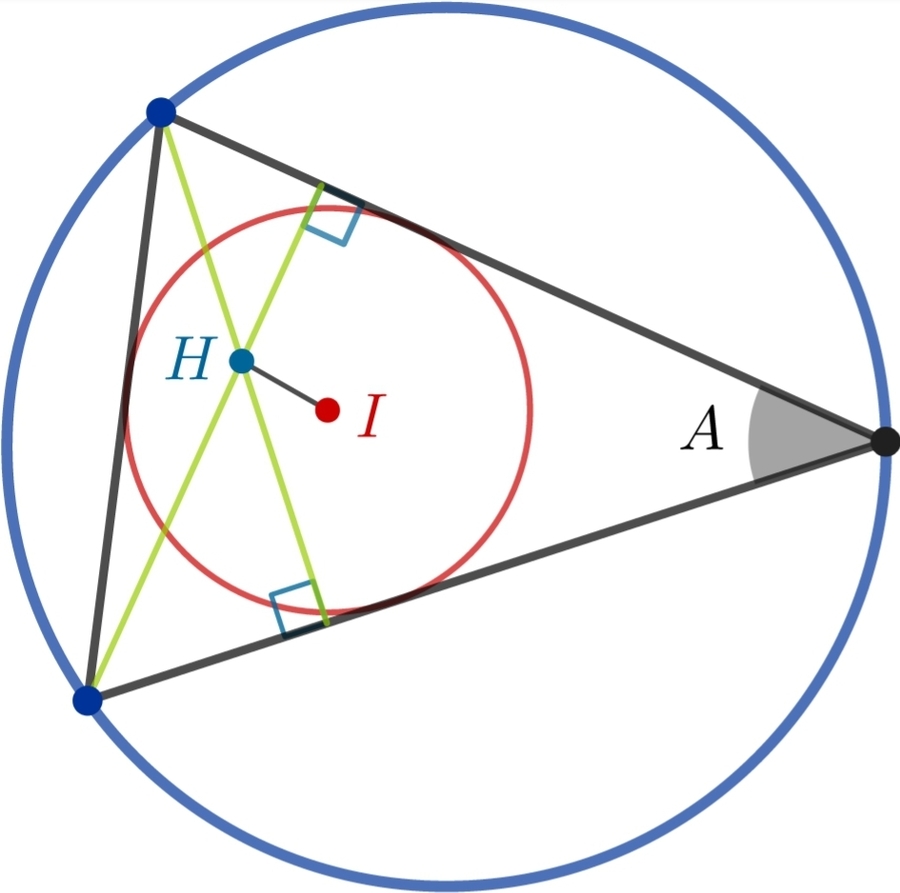 A triangle with a given angle
A
is inscribed in a
unit
circle.
A triangle with a given angle
A
is inscribed in a
unit
circle.
Let H I min denote the minimum possible distance between the orthocenter H and the incenter I of the triangle.
Let α = ∫ 0 2 π H I min d A .
Numerically evaluate the above integral after finding H I min as a function of A and submit your answer as the value of ⌊ 1 0 6 α ⌋ .
The answer is 246892.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Miraculous solution @Mark Hennings the x and u substitutions are simply brilliant, congrats! But would you explain why is r ² = 2 R ² ( 1 − c o s A ) ( 1 − c o s B ) ( 1 − c o s C ) ? Or is it just another identify I'm not aware of?
Also why is the constraint u < x there?
And (if it's not a too dumb question) what does the notation u ^ mean?
P.S.: How did you come up with these substitutions? Or they came naturally to you after countless solved problems?
Log in to reply
In the first, I am using the fact that r = 4 R sin 2 1 A sin 2 1 B sin 2 1 C , then squaring and using double angle formulae.
Since B + C = π − A , we obtain ∣ ∣ 2 1 ( B − C ) ∣ ∣ < 2 1 π − 2 1 A , and so cos 2 1 ( B − C ) > sin 2 1 A .
The quantity u ^ just means a particular value of u --- in this case u ^ = 4 u 2 − 1 2 u 3 .
Practice.
Log in to reply
Thank you for the explanation, but isn't it true B + C = π − A since B, C and A are angles of the triangle? Or you meant B − C < π − A ?
Log in to reply
@Veselin Dimov – Yes, I meant equality for B + C , which gives the inequality for (|B-C||).
The distance H I between the orthocentre H and the incentre I is given by the formula H I 2 = 2 r 2 − 4 R 2 cos A cos B cos C where r , R are the inradius and the outradius, respectively. Putting u = sin 2 1 A , x = cos 2 1 ( B − C ) , we see that 0 < u < x < 1 , and H I 2 = 4 R 2 [ ( 1 − cos A ) ( 1 − cos B ) ( 1 − cos C ) − cos A cos B cos C ] = 4 R 2 [ ( 1 − cos A ) − ( 1 − cos A ) ( cos B + cos C ) + ( 1 − 2 cos A ) cos B cos C ] = 4 R 2 [ 2 u 2 − 4 u 2 cos 2 1 ( B + C ) cos 2 1 ( B − C ) + 2 1 ( 4 u 2 − 1 ) ( cos ( B + C ) + cos ( B − C ) ) ] = 4 R 2 [ 2 u 2 − 4 u 3 x + ( 4 u 2 − 1 ) ( x 2 + u 2 − 1 ) ] In this case, R = 1 , and hence H I 2 = F u ( x ) = 4 [ ( 4 u 2 − 1 ) ( x 2 + u 2 − 1 ) − 4 u 3 x + 2 u 2 ] We thus want to minimize F u ( x ) over u < x < 1 for each 0 < u < 1 . Note that F u ′ ( x ) = 8 [ ( 4 u 2 − 1 ) x − 2 u 3 ] Note that there is a unique positive root 0 < β < 1 , with β ≈ 0 . 5 9 6 9 6 8 2 8 3 2 3 7 , of the cubic equation 2 X 3 − 4 X 2 + 1 = 0 . Now
If 0 < u < 2 1 then F u ′ ( x ) < 0 for all u < x < 1 , and so the infimum over u < x < 1 of F u ( x ) is F u ( 1 )
If 2 1 < u < β , then F u ′ ( x ) = 0 where x = u ^ = 4 u 2 − 1 2 u 3 , but the fact that u < β means that u ^ > 1 , and hence the infimum of F u ( x ) for u < x < 1 is F u ( 1 ) again.
If β < u < 2 1 , then F u has a turning point at u ^ defined as above, and u < u ^ < 1 , so the infimum of F u over u < x < 1 is F u ( u ^ ) .
If 2 1 < u < 1 then u ^ < u , and so the infimum of F u ( x ) over u < x < 1 is F u ( u ) .
Thus we deduce that H I min 2 = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ F u ( 1 ) = 4 u 2 ( 1 − 2 u ) 2 F u ( u ^ ) = 4 u 2 − 1 4 ( 1 − 2 u 2 ) 2 ( 3 u 2 − 1 ) F u ( u ) = 4 ( 2 u 2 − 1 ) 2 0 < u < β β < u < 2 1 2 1 < u < 1 and hence H I min = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ 2 sin 2 1 A ∣ ∣ 1 − 2 sin 2 1 A ∣ ∣ 2 cos A 4 sin 2 2 1 A − 1 3 sin 2 2 1 A − 1 2 ∣ cos A ∣ 0 < A < 2 sin − 1 β 2 sin − 1 β < A < 2 1 π 2 1 π < A < π Thus we calculate (numerically) α = ∫ 0 2 sin − 1 β 2 sin 2 1 A ∣ ∣ 1 − 2 sin 2 1 A ∣ ∣ d A + ∫ 2 sin − 1 β 2 1 π 2 cos A 4 sin 2 2 1 A − 1 3 sin 2 2 1 A − 1 d A = 0 . 2 4 6 8 9 2 3 5 3 7 which makes ⌊ 1 0 6 α ⌋ = 2 4 6 8 9 2 .