Minimized
1 4 1 x 2 + 3 x − 5
Find the real value of x such that the expression above is minimized.
The answer is -21.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great solution!
Just evaluate 2 a − b = − 3 ⋅ 7 = − 2 1 , which is the vertex of the parabola.
Similar solution as Ciprian Florea 's but in proper LaTex.
1 4 x 2 + 3 x − 5 = 1 4 1 ( x 2 + 4 2 x ) − 5 = 1 4 1 ( x 2 + 2 ( 2 1 ) x + 2 1 2 − 2 1 2 ) − 5 = 1 4 1 ( x + 2 1 ) 2 − 2 6 3 − 5 Since ( x + 2 1 ) 2 ≥ 0 ≥ − 2 7 3
1 4 x 2 + 3 x − 5 is minimum when x + 2 1 = 0 ⟹ x = − 2 1
Yeah, i use Daum Equation Editor :)))
Log in to reply
You can cut and paste the codes from Daum Equation Editor to appear properly on this web page. I edited your problem here and another one. You can put your mouse cursor over the formulas to see the LaTex codes. They are simplie.
Log in to reply
Yeah, in know, i've jus been too lazy, but i will do this from now on :)
Log in to reply
@Ciprian Florea – Good, if not the Brilliant's staff will have to edit them for you. I was given the right to edit problems to help the staff. I have just edited another one of your. Three now.
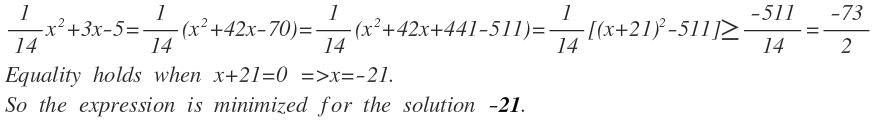
Let f ( x ) = 1 4 x 2 + 3 x − 5 :
f ′ ( x ) = 7 x + 3 f ′ ′ ( x ) = 7 1 > 0
f ′ ( x ) = 0 ⇒ 7 x + 3 = 0 ⇒ x = − 2 1
As f ′ ′ ( x ) > 0 this is a minimum so the answer is:
x = − 2 1