The Dark Side of x x
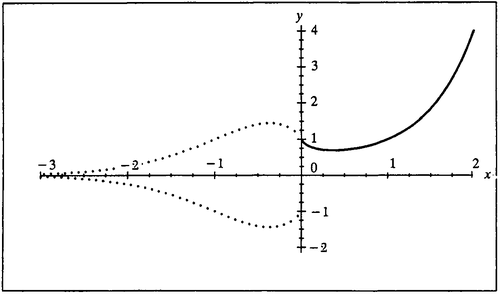
Let f ( x ) = x x be a real function of real variable x .
Find the infimum of f ( x ) .
To clarify, − 1 is a domain of f ( x ) because ( − 1 ) − 1 is a real number. But − 2 1 is not a domain of f ( x ) because ( − 2 1 ) − 2 1 is not a real number.
The answer is -1.44467.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
f is a real-valued function, but f(-e^(-1)) is a complex number and (-1)^x is not equal to -1 (for example, (-1)^(-2)=1 and (-1)^(-3)=-1, but there is another solution in complex plane)
Log in to reply
∀ x ∈ R , ( − 1 ) x ∈ R ⇒ ( − 1 ) x ∈ { 1 , − 1 } So I assumed ( − 1 ) x = − 1 since − 1 < 1 and we need to find minimum value
Also: ∀ x < 0 , f ( x ) ∈ R ⇒ f ( x ) = e x ln ( ∣ x ∣ ) o r f ( x ) = − e x ln ( ∣ x ∣ )
Log in to reply
the necessary condition is (-1)^x is in real, but (-1)^(-e^(-1)) is not real
Log in to reply
@Lingga Musroji – Well, ∀ x ∈ R − , x x ∈ R ⟺ ∃ m , n ∈ Z : ( x = n m ) ∧ ( 2 n ∈ Z )
So my we need to solve again, my solution is wrong
I am very much confused may be I don't know really the infimum thing, but if it is the greatest lower bound and according to this solution infimum is -1.444 But I want to know for which value of x it will be -1 or 0, because the domain of this function is itself x > 0 , I don't understand how do you arrive at the negative answer.
Log in to reply
To understand what happens when x < 0 , read the following paper: The x x spindle .
Log in to reply
Just read your question, it is not correct according to what you have defined. Since, it is R to R why are you considering imaginary numbers. I already posted a report regarding it
Log in to reply
@Aman Rajput – I have not considered imaginary numbers. Can you just apply your head and realize that f ( x ) gives out real values for x which are negative rational numbers whose denominators are odd.
For example f ( − 3 / 5 ) = − ( 1 2 5 / 2 7 ) 1 / 5 ≈ − 1 . 3 5 8 7
Log in to reply
@Digvijay Singh – Yes I tried that and I am getting real numbers.. nice
@Digvijay Singh
–
Hi Digvijay, please refrain from using disparaging phrases such as
Can you just apply your head
, it is not productive for any conversation.
@Aman Rajput – Read this paper to find the correct solution. Its a different paper.
Now edited the whole solution, maybe it's correct now
Log in to reply
Read this paper to find the correct solution.
Log in to reply
Isn't the solution above is also correct? (if their is any mistake in my solution then please let me know)
Log in to reply
@Zakir Husain – Yes, it is correct for the most part.
after look at the paper about x^x spindle (thanks for Digvijay Singh in above comment), now I understand how it works. But still, f is only defined for positive real number and negative rational with odd denominator (-p/q, p and q are positive and q is odd).
I think you should edit your question to make it clear, since you wrote the domain is real number
Log in to reply
Here's another paper which would make things more clear: Some Remarks on the Self-Exponential Function: Minimum Value, Inverse Function, and Indefinite Integral
Log in to reply
I understand. I'm talking about the given domain in the question, that is the real number (in the paper, the domain is positive real number and negative rational number with odd denominator)
How did you get − ∣ e − 1 ∣ e − 1 = − e e − 1 ?
Log in to reply
Oh, my mistyping, It was − ∣ − e − 1 ∣ − e − 1 now I edited the solution.
There is already a good solution posted here. I just want to provide an explanation of the "Considering" step for those that may need it.
The reason we can assert that ( − 1 ) x = − 1 is that such x values densely populate the real number line, which may first seem strange if the way you came to know Euler's formula, e i x = cos ( x ) + i sin ( x ) , is through alone the visual intuition of tracing a circle.
Let's consider an alternative way of evaluating ( − 1 ) x when rational x = b a ; ( − 1 ) x = ( ( − 1 ) a ) b 1 . Through this perspective, it becomes clear that if a is even, then ( − 1 ) x is any b th root of unity. Similarly, if a is odd, then ( − 1 ) x is any b th root of − 1 .
Because − 1 raised to an odd number equals − 1 , − 1 is always one of the values of ( − 1 ) x when both a and b are odd.
So when we assert that ( − 1 ) x = − 1 , we're assuming that x is a fraction whose numerator and denominator are both odd. And, again, this isn't an unreasonable assertion, because such fractions densely populate the real number line.
The density argument was definitely missing from the other solution when they consider x < 0 . The notion that for negative x < 0 they only consider rationals with odd denominator is also missing. All in all, f given is not actually defined on the entire reals. Nice explanation filling some gaps (pun intended)!
let lnf(x)=xln|x|
so f`(x)/f(x)=ln|x|+1
we got that f`(x)=(ln|x|+1) ·f(x)
then we let f`(x)=0 to find the extremum
we got that x= 1/e or -1/e
obviously,f(1/e )>f-1/e)
so the answer is f(-1/e) =-1.44467
New answer:
Obviously,if we want to find the infimum of f(x),we should talk about the situation when x < 0;
make t = -x,I think "let f(x) = x^x be a real function of real variable x" may means we should talk about g ( t ) = − t − t ,t>0
g ( t ) = − e − t l n t so g ′ ( t ) = ( l n t + 1 ) ⋅ e − t l n t
let f`(x)=0 to find the extremum,we got that t 0 = e 1
and g ( t 0 ) = − 1 . 4 4 4 6 7
Hi Somerest, your second line is already flawed.
Note that ln ∣ x ∣ = { ln ( x ) , ln ( − x ) , x > 0 x < 0
So you need to take more care in your second line onwards.
Log in to reply
Thanks for pointing out my mistake! Then What about my new answer.(My math is not so well,if it is wrong as well ,I will try to correct it)
Log in to reply
You might want to refer to the other solutions presented. You assumed that f ( x ) is continuous everywhere when it isn't.
Also note that f ( x ) is not defined when x = − e 1 .
Log in to reply
@Brilliant Mathematics – All right,I know what you mean,I have no idea about how to do now.I did some research,but I don`t know what is complex analysis yet
L e t x ∈ R − ⇒ x = ∣ x ∣ e i n π w h e r e n ∈ { x : x i s o d d i n t e g e r } ⇒ x x = ∣ x ∣ x e i n π x = ∣ x ∣ x ( cos ( x n π ) + i sin ( x n π ) ) ∵ x x ∈ R ∴ s i n ( x n π ) = 0 ⇒ x n ∈ N ⇒ x = n m w h e r e n ∈ { n : n i s o d d i n t e g e r , n = 0 } , m ∈ N x x ∈ R ⟺ ∃ p , q ∈ Z − { 0 } : ( x = q p ) ∧ ( 2 q ∈ Z ) n o w c o n s i d e r s o m e o d d i n t e g e r n : 0 > x = ∣ x ∣ e i n π x x = e x ln x = e x ( i n π + ln ∣ x ∣ ) = e x i n π × e x ln ∣ x ∣ = ( − 1 ) x ∣ x ∣ x ∈ { ∣ x ∣ x , − ∣ x ∣ x } ⇒ x x ∈ R ⟺ x x ∈ { ∣ x ∣ x , − ∣ x ∣ x } ⇒ ∀ x < 0 , x ≥ − ∣ x ∣ x = − e x ln ∣ x ∣ − x d e x ln ∣ x ∣ = 0 ⇒ − ∣ x ∣ x ( 1 + ln ∣ x ∣ ) = 0 ∵ ∣ x ∣ x = 0 ⇒ ln ∣ x ∣ = − 1 ⇒ ∣ x ∣ = e − 1 ⇒ x = − e − 1 ( ∵ x < 0 ) ⇒ ∀ x < 0 , x x ∈ R ⇒ x x > − ∣ − e − 1 ∣ − e − 1 = − e e − 1 = − 1 . 4 4 4 6 6 7 8 6