minimum in restricted area..
For 0 < x < π , find the minimum value of 2 x . s i n x 9 . x 2 . s i n 2 x + 4
Try more Trigonometry Problems
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Note: You should show that the equality case can indeed be achieved.
Log in to reply
The equality holds when 9 x s i n x = x s i n x 4 , ( x s i n x ) 2 = 9 4 , x s i n x = 3 2
sir are you asking about this thing
Log in to reply
You should state this can indeed be achieved. Technically, all that you have shown is that f ( x ) m i n ≥ 6 . You still need to show that f ( x ) m i n = 6 by finding a corresponding value of x .
Otherwise, as shown by this problem , if the equality case of AM-GM cannot be achieved, then the calculated value would not be the true minimum.
Log in to reply
@Calvin Lin – I think this is what you are asking for,
9 x 2 s i n 2 x − 1 2 x s i n x + 4 = 0 , ( 3 x s i n x − 2 ) 2 = 0 , x s i n x = 3 2
Sir now how do i find the value of x ?
Log in to reply
@U Z – You do not need to find the value of x . You just need to show that there exists a value of x which satisfies x sin x = 3 2 . This can be done, by using the Intermediate value theorem, since x sin x is a continuous function and 0 sin 0 = 0 , 2 5 π sin ( 2 5 π ) = 2 5 > 3 2 .
Exactly as it was expected...Good..Nice solution.
Log in to reply
Sir a good question on A.M - G.M inequality, asked in JOMO 10 , i can't post the question directly. I don't have the permission

My answer comes as 24 (hope our answer match)
JOMO 10 competition is finished (so i can discuss the question) , now JOMO 11 is the on-going competition
Log in to reply
Yeah, my answer is also 24. And that is achievable when x → 0 or y → 0 .. @megh choksi
Log in to reply
@Sandeep Bhardwaj – oh nice did'nt noticed, i did it this way
y [ 1 + x ( y 1 + y ) ] 2 + 3 y 2 + 3 x 2 y 2 ( y 1 + y ) 2 + 6 x y 2 ( y + y 1 )
= y [ 1 + x ( y 1 + y ) ] 3 y 2 ( x 2 ( y + y 1 ) 2 + 2 x ( y 1 + y ) + 1 ) + y [ 1 + x ( y 1 + y ) ] 2
= 3 y ( x ( y 1 + y ) + 1 ) + y [ 1 + x ( y 1 + y ) ] 2
A . M ≥ G . M
= 2 × 6 @Sandeep Bhardwaj thank you for being humble
I will have a look at this soon. By the way, can you tell me something about JOMO ? I don't have any idea about this ?
Log in to reply
Do you mean minimum value of the expression?
can be simplified as (9/2)xsinx + (2)/xsinx . ...........the range of xsinx= all real no.............let xsinx=a (any no.). .................so, we only need to find the min. of (9/2)a +(2)/a. ...................a=2/3 or min f(x)=6



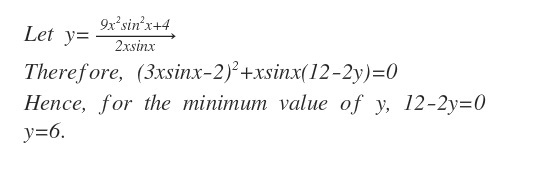
0 < x < π therefore sinx positive
f ( x ) = 2 9 x s i n x + x s i n x 2
2 2 9 x s i n x + x s i n x 2 ≥ 2 9 . 2 x s i n x x s i n x
f ( x ) m i n = 6