Mirror mirror on the graph

Calculus Level 5

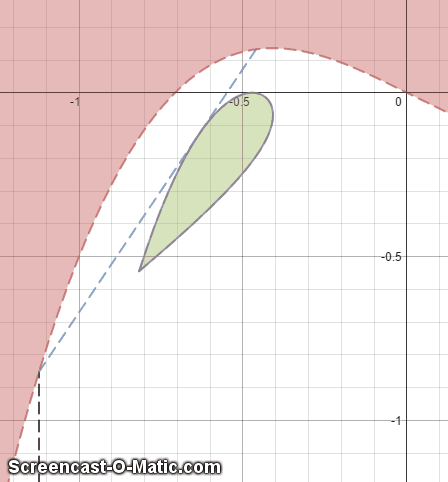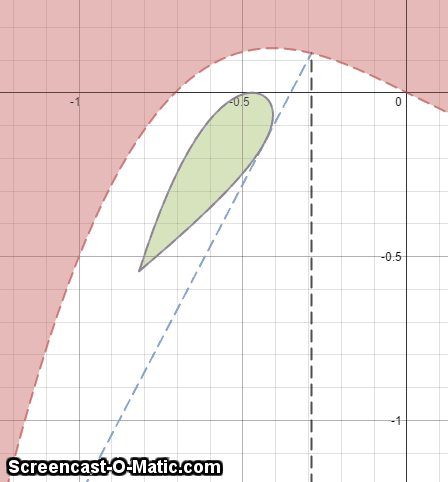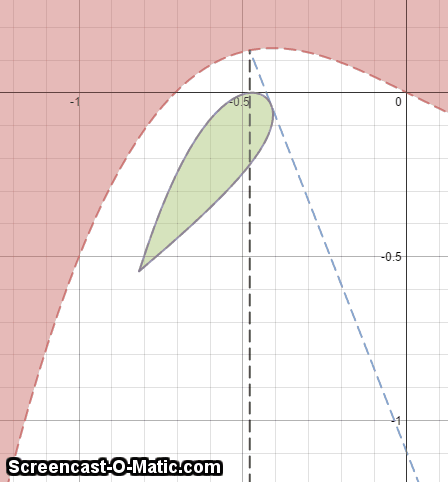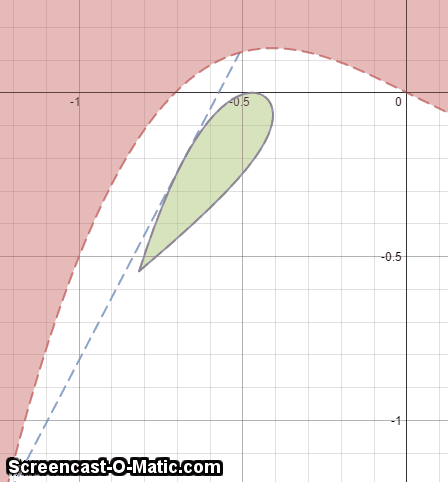
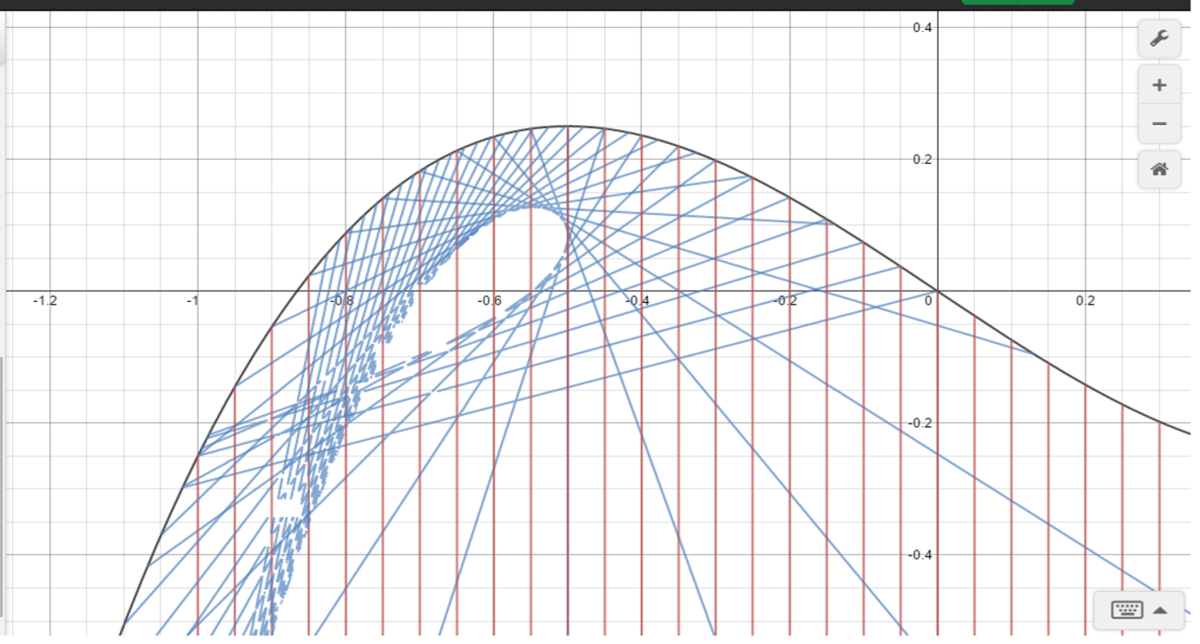
A mirror in the form of the graph function $x^{3}-0.5x$ (Shown in red in the GIF) is shone with parallel vertical rays of light from the bottom of the graph. The reflected rays of light form a droplet-shaped shape (shown in green in the GIF). Given that the area of that green shape is $A$ , find $\left\lfloor { 10 }^{ 8 } \times A \right\rfloor$

$\textbf{Details and Assumptions}$

$\bullet$ If the equation is of a semi circle ( $\sqrt{1-x^{2}}$ ):

You can solve this without any computational methods, but it is however, quite tedious. As such, you can use any computational methods, including Wolfram Alpha.

Try my Other Problems

The answer is 7932323.

1 solution

Michael Mendrin
Mar 27, 2015

The exact area is

$\dfrac { \sqrt { 3 } }{ 8 } +\dfrac { 5 }{ 192 } Log\left( 97-56\sqrt { 3 } \right)$

This is probably best done in parametric form.

Yep! In general, the parametric form of the reflection for the mirror-function $f(x)$ is $\left( t-\frac { f'\left( t \right) }{ f''\left( t \right) } ,\frac { 2f\left( t \right) f''\left( t \right) -f'\left( t \right) ^{ 2 }+1 }{ 2f''\left( t \right) } \right)$

Julian Poon - 6 years, 2 months ago

I had trouble in putting the limits for t in parametric form (Though Desmos helped and took my 1 hr to solve this). Can you please explain how to find the limits for t.

Akul Agrawal - 5 years, 5 months ago

Mind if you give me some details on what you mean on putting in the limits?

Julian Poon - 5 years, 5 months ago

@Julian Poon – I think what he means is that if this is to be integrated parametrically, what is the start and stop values of the parameter variable? I did work this out, but it's buried in my notes somewhere.

Michael Mendrin - 5 years, 5 months ago

@Julian Poon – I mean exactly what @Michael Mendrin sir say.

I got the parametric points as

$y={ t }^{ 3 }-0.5t+\frac { 1-{ \left( 3{ t }^{ 2 }-0.5 \right) }^{ 2 } }{ 12t } \\ x=\frac { 3{ t }^{ 2 }+0.5 }{ 6t }$

Then after integrating, what upper and lower values of t should I put?

( I found it by zooming desmos graph)

Akul Agrawal - 5 years, 5 months ago

@Akul Agrawal – I forgot how exactly I did it last time, but what you can do is to (tediously) convert the parametric equation into

$y=g(x)=\frac{1}{18}\left(18x^3+3\sqrt{6}\sqrt{6x^2-1}x^2-2\sqrt{6}\sqrt{6x^2-1}\right)$

$y=h(x)=\frac{1}{18}\left(18x^3-3\sqrt{6}\sqrt{6x^2-1}x^2+2\sqrt{6}\sqrt{6x^2-1}\right)$

Then, to find the point in which these two graphs intersect, solve for

$g(x)=h(x)$

Which give out $x=\sqrt{\frac{2}{3}}$

Substituting that into the parametric equation gives

$\sqrt{\frac{2}{3}}-\frac{1}{\sqrt{2}}\le t\le \sqrt{\frac{2}{3}}+\frac{1}{\sqrt{2}}$

I did use wolfram extensively to reduce the tediousness.

Julian Poon - 5 years, 5 months ago

@Julian Poon – Thanx. Let's see if it can be easier!

Akul Agrawal - 5 years, 5 months ago

@Akul Agrawal – Btw, don't call me sir, I'm actually younger than you.

Julian Poon - 5 years, 5 months ago

@Julian Poon – Please update your profile

Akul Agrawal - 5 years, 5 months ago

@Julian Poon – what's your age then

Akul Agrawal - 5 years, 5 months ago

@Akul Agrawal – Age 15, and I don't plan on updating my profile.

Julian Poon - 5 years, 5 months ago

@Julian Poon – Oh nyc... You do such great questions at this age.

Akul Agrawal - 5 years, 5 months ago

@Akul Agrawal – you may like this

Akul Agrawal - 5 years, 5 months ago

How did you solve it??? (The easiest method you can think of??)

Sualeh Asif - 6 years, 2 months ago

Envelope

It is a madly powerful method.

Julian Poon - 6 years, 2 months ago

1) First find parametric equations $x\left( t \right) ,y\left( t \right)$
2) Find $t=a$ and $t=b$ where it self intersects
3) Compute $Area=\int _{ a }^{ b }{ x\left( t \right) } y'\left( t \right) dt=\int _{ a }^{ b }{ x'\left( t \right) } y\left( t \right) dt$

Poon gives the general expression for finding the parametric equation for reflection envelope, even though I wasn't aware of one.

Michael Mendrin - 6 years, 2 months ago

The only reason why I derived for a general case was because I wanted to make a simulator . I've ran out of interesting reflection envelopes. There are some interesting ones like $f(x)=tan(x)$ and $f\left(x\right)=\left(1-x^b\right)^{b^{-1}}$ and $f(x)=e^{x-1}$ . I especially liked the last one.

Julian Poon - 6 years, 2 months ago

@Julian Poon – That looks like a really cool graphing calculator. I was wondering how you got the nice animated graphics.

Somewhere buried in my pile of books, I still have a book of curves and all the associated curves that go with them, like glissettes, evolutes, caustics, etc. Now you can look it up for free. Your problem involves the caustic of the cubic.

A Book of Curves

Michael Mendrin - 6 years, 2 months ago

@Michael Mendrin – Wow! Thanks!

Julian Poon - 6 years, 2 months ago

I had trouble in putting the limits for t in parametric form (Though Desmos helped and took my 1 hr to solve this). Can you please help with the limits.

Akul Agrawal - 5 years, 5 months ago

Mirror mirror on the graph

The answer is 7932323.

1 solution

0 pending reports