Mirror, mirror, on the wall, who's the fairest of them all?

Computer Science Level 5

A positive integer $n$ is called fair if the sum of the factorial of its digits is divisible by itself. 145 is one such number : $1! + 4! + 5! = 145 \equiv 0 \pmod {145}$ Find the sum of all the fair numbers less than $10^7$ .

The answer is 99797.

5 solutions

Samarpit Swain
Aug 21, 2015

Fun problem! The following C++ returns the list of numbers that satisfy the given conditions. it can be easily modified to provide the sum of these.

#include<iostream.h> 
#include<conio.h>
#include<math.h>
void main()
  {   unsigned long int num,dig,fact;
               clrscr();

   for(unsigned long int  x=1;x<=10000000;x++)
  {     num=x;
         unsigned long int sum=0;

    while(num>0)  
{   dig=num%10;
      fact=1;

 for(int i=1;1<=dig;i++)
{     fact=fact*i;
                        }

sum+=fact;
num=num/10;

                                 }
if(sum%x==0)
cout<<x<<endl;
                                       }
         getch();  
 }

Abdelhamid Saadi
Aug 19, 2015

for the seek of optimization only.

let $f(n)$ be the sum of the factorial of all the digits of $n$ . we can easily that : $f(n) \leq 9! \times (log(n) +1)$ $n \leq f(n)$

So that n must be less that a certain value(in fact 6028144).

Solution in python 3.4:

from math import factorial as fact
from math import log
def g(n):
    return n/(log(n)+1)

def computemax():
    b = 1
    while g(b) < fact(9):
        b = 2*b
    a = b//2
    while a > 0:
        b = (b if g(b - a) < fact(9) else b -a)
        a = a//2
    return b

def isfair(n):
    return sum([fact(int(d)) for d in str(n)])%n == 0

def solve(n):
    "Mirror, mirror, on the wall, who's the fairest of them all?"
    a = min(n, computemax())
    return sum([n for n in range(1,computemax()) if isfair(n)])

print(solve(10**7))

Bill Bell
Aug 18, 2015

from math import factorial

facts={k:factorial(k) for k in range(10)}

N=10**7
total=0
for n in range(1,N):
    total+=n if sum([facts[k] for k in map(int,list(str(n)))])%n==0 else 0

print total

It can be shown that the sequence is finite, with a maximum value of 40585.

D G - 5 years, 9 months ago

Please provide a reference.

Bill Bell - 5 years, 9 months ago

We're looking for numbers $n$ such that the sum of the factorials of the digits ( $f(n)$ ) is greater than or equal to $n$ . The largest value of $f(n)$ for a $d$ digit $n$ occurs when $n$ is all 9's ( $f(9999) = 4*9! = 1451520$ ). $f(99999999) = 8*9! = 2903040$ , a seven digit number. Since any larger sequence of 9's must have a larger digit sum, we conclude that $7*9! = 2540160$ is an upper bound for the sequence.

D G - 5 years, 9 months ago

@D G – I might still be missing your point. I believe we're looking for the sum of a certain collection of fine numbers.

Bill Bell - 5 years, 9 months ago

Arulx Z
Sep 5, 2015

I stores the values of factorial of digits from $0$ to $9$ in an array. This is because in base $10$ , they are the only existent digits. Since I don't compute them everytime, it makes my code much faster. Here is my code -

n = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880]
summ = 0
for x in xrange(1, 10000000):
    summ += x if sum(n[int(i)] for i in str(x)) % x == 0 else 0
print summ

There is a lot of space for optimization. See Abdelhamid Saadi's answer for example. Also memorization and skip counting in some cases will improve the speed too. I'm working on improving my code. I'll post when it's done!

Aareyan Manzoor
Sep 20, 2015

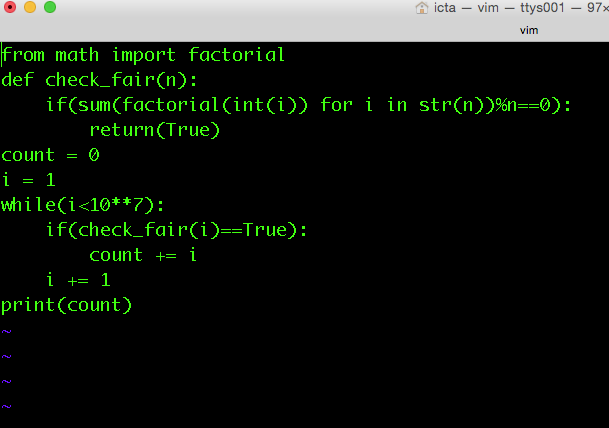any quicker solutions for python??

Mirror, mirror, on the wall, who's the fairest of them all?

The answer is 99797.

5 solutions

0 pending reports