Geometriculus?
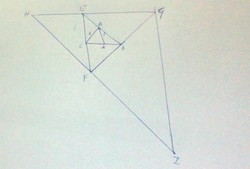 Getting bored in my history class I started drawing some amazing triangles .
Getting bored in my history class I started drawing some amazing triangles .
Starting from to then to and then again to (loop). Now extending to such that . Joining and extending to such that . Again joining and and extending to such that and so on indefinitely without lifting the pen (as shown in figure).
Denote the following symbols:
be the set containing lines parallel to .
be the set containing lines parallel to .
be the set containing lines parallel to or .
be the set containing lines parallel to or .
As i was getting extremely bored i drew 59 lines (assume)
We further denote the following:
Now the monic quartic equation whose roots are is "double derivated" (double differentiated) and it can be represented as .
Find the value of .
Details and Assumptions
-
are also included in the corresponding sets.
-
Consider and so on single line segments instead of two line segments.
This is original and the incident did happen.
The answer is 3000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, define L n as the n t h line drawn by the speaker, so that L 1 = A B , L 2 = B C , L 3 = C D , L 4 = D E , and so forth. Notice that L 1 ∣ ∣ L 5 , L 2 ∣ ∣ L 6 , L 3 ∣ ∣ L 7 , a n d L 4 ∣ ∣ L 8 . More generally, L n ∣ ∣ L n + 4 , so the set of lines parallel to L n will include all lines L m where m ≡ n ( m o d 4 ) and m ≤ 5 9 since the speaker drew only 59 lines. This now gives
γ = { L 1 , L 5 , L 9 , . . . , L 5 7 } , n ( γ ) = 1 5
β = { L 2 , L 6 , L 1 0 , . . . , L 5 8 } , n ( β ) = 1 5
Δ = { L 3 , L 7 , L 1 1 , . . . , L 5 9 } , n ( Δ ) = 1 5
Θ = { L 4 , L 8 , L 1 2 , . . . , L 5 6 } , n ( Θ ) = 1 4
so the quartic polynomial with the above numbers as its roots will be of the form c ( x − 1 5 ) 3 ( x − 1 4 ) where c is a constant. For the purpose of this solution, let c = 1 so that the needed polynomial is ( x − 1 5 ) 3 ( x − 1 4 ) = x 4 − 5 9 x 3 + 1 3 0 5 x 2 − 1 2 8 2 5 x + 4 7 2 5 0 . Differentiating this polynomial twice gives d x 2 d 2 ( x − 1 5 ) 3 ( x − 1 4 ) = 1 2 x 2 − 3 5 4 x + 2 6 1 0 .
Finally, the answer is obtained by adding 1 2 + 3 5 4 + 2 6 1 0 + 2 4 = 3 0 0 0