Nine is the key
Let f ( x ) denote the sum of digits of integer x . Find the value of f ( f ( f ( 5 1 0 0 0 0 ) ) ) .
As an explicit example, f ( 5 3 ) = f ( 1 2 5 ) = 1 + 2 + 5 = 8 .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great proof!
Yup! You just proved the divisibility rule of 9.
Log in to reply
Is my proof about this problem wrong?
Log in to reply
Needs a little bit of formatting but it's alright!! Thanks!
According to the question we need to find sum of 5 n three times. Let us observe the pattern of sum three times :
5 1 = 5
5 2 = 7
5 3 = 8
5 4 = 4
5 5 = 2
5 6 = 1
5 7 = 5
we found that its cyclicity is 6,
so answer is 4
I don't understand why it has to cycle, and even if it cycles m o d 1 0 , what this solution is missing is to show that f ( f ( f ( 5 1 0 0 0 0 ) ) ) is a single digit number.
How do we know the answer is not 13? 1 3 ≡ 4 ( m o d 9 ) .
@Dev Sharma Well, are you going to fix your solution?
Log in to reply
Which part is missing?
Log in to reply
The proof that f ( f ( f ( 5 1 0 0 0 0 ) ) ) has 1 digit only.
Log in to reply
@Sharky Kesa – 5 1 0 0 0 0 has at most 9999 digits whose sum is at most 89991 ⇒ f(f(89991)= 9 ⇒ the answer really has one digit
Log in to reply
@Guillermo Templado – Yes, thats what I was looking for!
Log in to reply
@Julian Poon – No, I'm not right,for example f(f(59347))= f(28) = 10. I'll think later about this, the solution can be 13 or 22 how you or Sharky told, even 31
Log in to reply
@Guillermo Templado – Oh yeah, thats true. Any x that is bigger of equal to 19999999999999999999999, f(f(f(x))) might be equal to 10 or more.
@Julian Poon – A bound is required. That's the only missing part in the solution.
@Sharky Kesa – This is what I have shown through cyclicity
Log in to reply
@Dev Sharma – No you haven't. This proof is only for ( m o d 1 0 ) . If it isn't, how do you know that this pattern breaks down for some large integer n . For instance:
f ( f ( f ( 4 55555 9 ’s 9 9 9 . . . 9 9 9 ) ) ) = 1 3 = 4
@Dev Sharma – You have only shown that it repeats mod 10, you have not shown that it would be a single digit. The answer for this question is a single digit only because 5 1 0 0 0 0 isn't a big enough number to obtain a bigger number.
Log in to reply
@Julian Poon – I have not shown that it repeats mod 10, i have shown 3 times sum of 5^n
Log in to reply
@Dev Sharma – Yes, you have shown it repeats in ( m o d 1 0 ) . Also, if it is not in ( m o d 1 0 ) where is your proof that this cyclicity occurs for all powers of 5 (even extremely large powers)? Your solution only shows that the first few powers satisfy.
Log in to reply
@Sharky Kesa – Please show your proof
Log in to reply
@Dev Sharma – We're only saying that your solution is wrong and requires working on.
@Dev Sharma – So you're not going to fix it then?
Nice problem 👌
Like others are saying you must show that the answer is single digit. For that we can calculate the number of digits in the number which is 10000log5=6990 which has a maximum sum of 6990×9=62910. This means that if we take digit sum thrice it has to be a single digit number and then you can use your pattern.
Log in to reply
Finding the upper bound for f ( 5 1 0 0 0 0 ) is not enough, because f ( f ( 6 2 9 1 0 ) ) is not necessary the biggest it can get. Consider f ( f ( 1 9 9 9 9 ) ) . It is bigger than f ( f ( 6 2 9 1 0 ) ) despite 6 2 9 1 0 > 1 9 9 9 9
Log in to reply
Yes I realized that after I wrote the comment and it is also pointed out by Guillermo Templado. Maybe you can help to make it a complete solution.
See problem 4 of the 1975 IMO .
The solution can be imitated
Solving f(5^1000) with C++
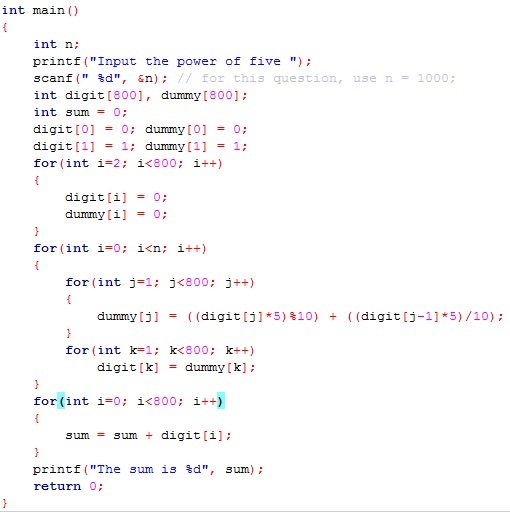
Does it also work for n = 32,768 or n = 2,147,483,648 .. ?
Proposition.- n ≡ f ( n ) ( m o d 9 ) for each n natural number
Proof.- Let
n = a b c d e = e + 1 0 d + 1 0 0 c + 1 0 0 0 b + 1 0 0 0 0 a
⇒ f ( n ) = a + b + c + d + e ⇒ 9 ∣
n − f ( n ) = 9 d + 9 9 c + 9 9 9 b + 9 9 9 9 a .
This reasoning can be generealized...Q.E.D
So 5 1 0 0 0 0 ≡ f ( 5 1 0 0 0 0 ) ( m o d 9 ) .
5 1 0 0 0 0 = ( 5 4 ) 2 5 0 0 ≡ 4 2 5 0 0 ( m o d 9 ) ⇒ 4 2 5 0 0 = 4 ⋅ ( 4 3 ) 8 3 3 ≡ 4 ⋅ 1 8 3 3 ≡ 4 ( m o d 9 ) ⇒ 5 1 0 0 0 0 ≡ 4 ( m o d 9 ) .
Since 5 1 0 0 0 0 has at most 9999 digits and 9 ⋅ 9 9 9 9 =89991, 1< f( 5 1 0 0 0 0 ) < 89991 < 99999, so f( 5 1 0 0 0 0 ) has at most 5 digits ⇒ 1 < f(f( 5 1 0 0 0 0 )) < 45, ( f(f( 5 1 0 0 0 0 )) ≡ 4 (mod 9) ) ⇒ f(f( 5 1 0 0 0 0 )) = 4, 13, 22, 31 or 40( They add all the same) ⇒ f(f(f( 5 1 0 0 0 0 ))) = 4