A number theory problem by Prem Chebrolu

To solve this problem, we need to find $9(1^{33}+2^{33}+3^{33}+4^{33}+5^{33}+6^{33}+7^{33}+8^{33}+9^{33}) \text{(mod 10)}$ . There are 5 odd numbers and 4 even numbers in the sum which means that the sum is odd. 9 times the sum will also be odd therefore 5 is the only possible answer from the choices given.

Simpler solution :

$\begin{aligned} S & \equiv {\color{#3D99F6}1^{33}} + {\color{#D61F06}2^{33}} + {\color{#3D99F6}3^{33}} + \cdots + {\color{#D61F06}44^{33}} + 45^{33} + {\color{#D61F06}46^{33}} + \cdots + {\color{#3D99F6}87^{33}} + {\color{#D61F06}88^{33}} + {\color{#3D99F6}89^{33}} \text{ (mod 10)} \quad \quad \small \color{#3D99F6} \text{Pair the respective end terms together.} \\ & \equiv {\color{#3D99F6}1^{33}} + {\color{#3D99F6}89^{33}} + {\color{#D61F06}2^{33}} + {\color{#D61F06}88^{33}} + {\color{#3D99F6}3^{33}} + {\color{#3D99F6}87^{33}} + \cdots + {\color{#D61F06}44^{33}} + {\color{#D61F06}46^{33}} + 45^{33} \text{ (mod 10)} \\ & \equiv {\color{#3D99F6} (1+89) \sum_{k=0}^{32}(-1)^k 1^k 89^{32-k}} + {\color{#D61F06} (2+88) \sum_{k=0}^{32}(-1)^k 2^k 88^{32-k}} + {\color{#3D99F6} (3+87) \sum_{k=0}^{32} (-1)^k 3^k 87^{32-k}} + \cdots + {\color{#D61F06} (44+46) \sum_{k=0}^{32}(-1)^k 44^k 46^{32-k}} + 45^{33} \text{ (mod 10)} \\ & \equiv 90 \sum_{k=0}^{32}(-1)^k 1^k 89^{32-k} + 90 \sum_{k=0}^{32}(-1)^k 2^k 88^{32-k} + 90 \sum_{k=0}^{32} (-1)^k 3^k 87^{32-k} + \cdots + 90 \sum_{k=0}^{32}(-1)^k 44^k 46^{32-k} + 45^{33} \text{ (mod 10)} \\ & \equiv 0 + 45^{33} \text{ (mod 10)} \\ & \equiv \boxed{5} \text{ (mod 10)} \end{aligned}$

---

Previous solution:

We need to find $S \bmod 10$ . Then

$\begin{aligned} S & \equiv \sum_{k=1}^{89} k^{33} \text{ (mod 10)} \\ & \equiv \sum_{j=0}^8 \sum_{k=1}^9 (10j+k)^{33} \text{ (mod 10)} \\ & \equiv 9 \sum_{k=1}^9 k^{33} \text{ (mod 10)} = - \sum_{k=1}^9 k^{33} \text{ (mod 10)} \\ & \equiv - \left(1^{33} + 2^{33} + 3^{33} + 4^{33} + 5^{33} + 6^{33} + 7^{33} + 8^{33} + 9^{33} \right) \text{ (mod 10)} \\ & \equiv - \left((1^{33} + 9^{33}) + (2^{33} + 8^{33}) + (3^{33} + 7^{33}) + 4^{33} + 6^{33}) + 5^{33} \right) \text{ (mod 10)} \quad \quad \small \color{#3D99F6} \text{See note.} \\ & \equiv - \left((1+ 9)\sum_{k=0}^{32} (-1)^k 1^{32-k}9^k + (2+ 8)\sum_{k=0}^{32} (-1)^k 2^{32-k}8^k + (3+ 7)\sum_{k=0}^{32} (-1)^k 3^{32-k}7^k + (4+ 6)\sum_{k=0}^{32} (-1)^k 4^{32-k}6^k + 5^{33} \right) \text{ (mod 10)} \\ & \equiv - \left(10\sum_{k=0}^{32} (-1)^k 1^{32-k}9^k + 10\sum_{k=0}^{32} (-1)^k 2^{32-k}8^k + 10\sum_{k=0}^{32} (-1)^k 3^{32-k}7^k + 10\sum_{k=0}^{32} (-1)^k 4^{32-k}6^k + 5^{33} \right) \text{ (mod 10)} \\ & \equiv - 5^{33} \equiv - 5 \equiv \boxed{5} \text{ (mod 10)} \end{aligned}$

$$

---

Note : $\displaystyle (a^n+b^n) = (a+b) \sum_{k=0}^{n-1} (-1)^k a^{n-1-k}b^k$ , where $n$ is an odd positive integer.

$S =1^{33} + 2^{33} + 3^{33} + 4^{33} + \cdots+ 89^{33}$ To determine the last digit the sum above we just need to determine the last digit of each number from 1 to 9 and note that $33\equiv 1 \mod (4)$ . Therefore, $\small 1^{33} + 2^{33} + 3^{33} +\cdots + 9^{33} = 1^1+ 2^1+3^1+\cdots +9^1 =4{\color{#3D99F6}5} \\ \small 1^{33+}2^{33}+3^{33}+\cdots +89^{33} =1^1+2^1+3^1+\cdots+89^1 = 400{\color{#3D99F6}5}$ Therefore, the answer is $5$ .

For similar problem click here

Work modulo 10; then the answer is $9 \times (1^{33} + 2^{33} + \dots + 9^{33})$ . But $9 \equiv -1 \pmod{10}$ , $8 \equiv -2 \pmod {10}$ , etc., so we can rearrange in pairs: $9 \times (1^{33} + (-1)^{33} + \dots)$ . Since 33 is odd, $(-n)^{33}=-n^{33}$ and the pairs all cancel. The only unpaired number is 5, so the answer is $9 \times 5^{33} \pmod {10}$ , which must be 5 since all powers and odd multiples of 5 end in 5.

$1^{33}=1$ so it's last digit is $1$ itself.

---

If we calculate the powers of $2$ , we get $2,4,8,1\boxed{6},3\boxed{2}...$ , So after every 4 terms the unit place digits are repeated.

So $2^{33}$ ends with the digit $2$ because remainder of $\dfrac{33}{4} = 1$ .

---

If we calculate the powers of $3$ , we get $3,9,2\boxed{7},8\boxed{1},24\boxed{3}...$ , So after every 4 terms the unit place digits are repeated.

So $3^{33}$ ends with the digit $3$ because remainder of $\dfrac{33}{4} = 1$ .

---

It will hence be same for all other numbers till $9$ . The numbers are repeated periodically with a period of $4$ .

---

The conclusion I want to make is that " For the power of 33, all the numbers have the same unit place digit as the number itself "

---

Our work is simple after all the hustle, just add $(1+2+3+...+9)$ which is equal to $45$ whose unit place is occupied by $\boxed{5}$

We have to use an Euler's equation to solve this. 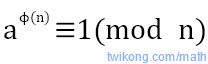while $(a,n)=1$ so, we can get that (it is possible because even if a's unit digit is 0, it is right)

For this problem I put it to mod 2:

1. First thing I noticed is that every 4 consecutive numbers is 0 mod 2

2. Also raising powers change nothing mod 2

$S = 1^{33} + 2^{33} + 3^{33} + \ldots + 89^{33}$ $\Rightarrow S \equiv 1 + 2 + 3 + \ldots + 80 + 89 \pmod{2}$

Then I will make it into pairs of four consecutive numbers and I'll have one remaining number unpaired

$S \equiv 89 \pmod {2}$

$S \equiv 1 \pmod {2}$

So I immediately see that there is only one choice that goes with condition

$\boxed{S \equiv 5 \pmod{10}}$

Fact 1: Only the unit digit of those numbers in the sum does matter.

Fact 2: A interesting result is that $n^{k}\mod10 = n^{k\mod4}\mod10$ .

With that on mind we can notice that it ends up being equivalent to :

$[1 + 2 + 3 + 4 + \cdots + 89] \mod 10$

Also, there's a very known formula for the partial sum between naturals wich lead us to :

$(\frac{89 \times 90}{2}) \mod10$

Turns out that $(\frac{89 \times 90}{2}) \mod10$ is 5

Any power which is in form of 4N+1 give same unit digit as unit digit of base number. 32=4N+1 1^32==1 unit digit 2^32==2 unit digit 3^32==3 unit digit And so on.. adding 1+2+3+4+5+6+7+8+9=0+5=5 for 1 to 10 1+2+3+4+5+6+7+7+9=0+5=5 for 11 to 20 So 1 to 89=> 5+5+5+5+5+5+5+5+5=0+5 =0+5 =5 unit digit.

The only parts of the problem that effect the outcome of the problem, the units digits, are the units digits of each of the original numbers. All powers have cyclings of units digits since all of them have a units digit multiply itself. For example, for powers of 2, it will be 2,4,8,16,32,64,128,256, etc. Extracting the units digits from the cycle, and you get standard cycling of units digits for any powers of any number ending in a certain digit. Thus, all we have to examine is the cycles of all the units. For all the powers of numbers ending in all the ten digits, the cycles are the following (By the way, determining these cycles amounts to continuously multiply each power one by one, determining the units digit, ignoring all the other digits, and multiply the power by the next unit digit, and so on.):

0: 0 (numbers ending in 0 can be ignored because they always end up with 0 units digits, so they don't contribute to the final units digit)

1: 1 (Period = 1)

2: 2 -> 4 -> 8 -> 6 -> 2 (Period = 4)

3: 3 -> 9 -> 7 -> 1 -> 3 (Period = 4)

4: 4 -> 6 -> 4 (Period = 2)

5: 5 (period =1)

6: 6 (period = 1)

7: 7 -> 9 -> 3 -> 1 -> 7 (Period = 4)

8: 8 -> 4 -> 2 -> 6 -> 8 (Period = 4)

9: 9 -> 1 -> 9 (Period = 2)

Now, there are 9 of each digit in the sum of all those powers of 33, and also, the units digit outcome for each units digit number is determined by the 33rd number in the cycle. This can be done with the period of the cycle by using mod of the period:

33 mod 4 =1

33 mod 2 = 1

33 mod 1 = 1

Thus, all the units digits appear as themselves. In other words, the final units digit is the units digit of this outcome:

9 * (1+2+3+4+5+6+7+8+9)

Using outer pairs, the sum becomes a bunch of tens, besides the remaining 5. 9 times 5 is 45, which ends in 5, so the answer is 5.

Since an odd number to an integer power is odd, and an even number to an integer is even, you can deduce if S is even or odd. Since there is an odd number of odd terms (45), all of the odd terms sum up to an odd number. An odd number plus any number of even numbers is still an odd number, so therefore S must be an odd number. Since 5 is the only odd number presented and one of these answers provided must be correct, 5 must the correct answer.

Easiest solution ever: There is only one odd number in the multiple choice options, "5." If you can prove the solution is odd, that is your answer.

• Adding an odd number to an even number results in an odd number.

• Multiples of odd numbers with odd numbers are also odd.

• Adding an odd number to an odd number results in and even number.

Therefore, if you have an odd number of odd n^33 values being added together, the result is odd. $\frac{88}{2}+1=45$ odd values being added.

Therefore the solution is odd.

Therefore, the solution is 5.

Powers of the last digits of base 10 numbers cycle through no more than four iterations... that is:

$1^{1}\equiv 1^{5}\equiv 1^{9}\equiv ... \equiv 1^{33}\equiv 1$ (mod 10).

$2^{1}\equiv 2^{5}\equiv 2^{9}\equiv ... \equiv 2^{33}\equiv 2$ (mod 10).

$3^{1}\equiv 3^{5}\equiv 3^{9}\equiv ... \equiv 3^{33}\equiv 3$ (mod 10).

...

$9^{1}\equiv 9^{5}\equiv 9^{9}\equiv ... \equiv 9^{33}\equiv 9$ (mod 10).

The last digit of numbers 1 through 10 is the last digit of 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0, which is 5. Multiply this by nine for 1 through 89, and the last digit is 5.

At First notice that the first and the last and the second and the forelast (and so on) summand always adds up to $90^{33}$ so that you get $44* 90^{33} + 45^{33}$ which is equal to $4005^{33}$ . You can now split it into $4000^{33} + 5^{33}$ . $4000$ raised to any power won't effect the units digit, $5$ raised to a power always leaves a $5$ as the units digit with means that the units digit of S is $\boxed5$

Since the unit digit of 1^33 is 1. And for 2^33 is 2 as 2 has a repeating unit digit in powers ex 2^1=2,2^2=4,2^3=8,2^4=16,2^5=32 we see that it has repetition of unit digit after every 4 powers therefore unit digit of 2^33 is 2 similarly 3 is 3 for 4^33 is 4 till 89^33 is 89 this implies the unit digit is 1+2+3.....+89 which = 4005 whose unit digit is 5.

1 raised to any power is 1. Powers of 2 end in either 2, 4, 8 or 6, meaning that the 33rd power of 2 ends in 2. Powers of 3 end in 3, 9, 7 or 1, so the 33rd power of 3 ends in 3. Powers of four end in 4 or 6, so the 33rd power of four ends in 4. Five and six are both automorphic numbers - their powers always end in five (for five) and six (for six). Powers of 7 end in 7, 9, 3 and 1, so again the 33rd power of 7 ends in 7. Powers of 8 end in 8, 4, 2 and 6, again four end numbers, meaning that the 33rd power of eight ends in eight. Powers of nine end in 9 or 1, so the 33rd power of 9 ends in 9. Extending this through the rest of the numbers, the last digit of each 33rd power is the last digit of the number itself. Thus, the last digit of the sum of these powers will be the last digit of the sum the numbers 1 to 89 inclusive, which using the formula that Gauss famously derived as a schoolboy is 4005. Thus the answer is 5. Incidentally it took much longer to write this explanation than it did to get the answer, for which I did not even require paper and pencil, let alone anything more sophisticated.

1^33+2^33+3^33+......+89^33= To find the last digit of sum ,add the last digit of each no. For ex. 1^33=1 2^33=2^(32+1)=2^32×2=last digit will be(2) Bcaus 2^1=2 2^2=4 2^3=8 2^4=16 last digit(6) 2^5=32 last digit(2) So. 2^4n×2=last digit(2) Similarily for 3^4n=last digit(1) So. 3^32×3=last digit(3) 1^33+2^33+3^33+.......+89^33=1+2+3+4+...+89 =(89×90)/2 USING(N(N+1))/2 =4005(sum of last digits) =last digit(5)

Here's an approach by which you can solve the problem in your head!

First we notice that only the units digits matter, so we need only consider the terms $1^{33} + \cdots + 9^{33}$ , and each term appears nine times. For each of the digits 1 - 9, we also must see that the units digit repeats every four multiplications. To demonstrate this, I've listed out the units digits of the first five powers of each of the digits 1 - 9 here:

{1, 1, 1, 1, 1} {2, 4, 8, 6, 2} {3 9 7 1 3} {4 6 4 6 4} {5 5 5 5 5} {6 6 6 6 6} {7 9 3 1 7} {8 4 2 6 8} {9 1 9 1 9}. Notice that the units digit of $N^5$ always equals $N^1$ .

Since the units digits repeat every four multiplications, the units digit of $N^{33}$ is just $N$ for any digit $N$ . Now we just have to sum our terms (only keeping track of the units digit of the sum.) The 1s and 9s together give 0, the 2s and 8s together give 0, the 3s and 7s together give 0, and the 4s and 6s together give 0. So the only terms contributing to the final units digit are the nine 5s, which total 45, making our final units digit 5 .

Since we are dealing with $\mod{10}$ , we simplify the problem by taking only the last digit and preserving the power.

e.g. $34^{33} \equiv 4^{33}\mod{10}$ ; $48^{33} \equiv (-2)^{33}\mod{10}$ .

Everything simplifies to

$1^{33} + 2^{33} + \cdots + 89^{33} \equiv 9(1^{33} + 2^{33} + 3^{33} + 4^{33} + 5^{33} - 4^{33} - 3^{33} - 2^{33} - 1^{33}) \mod{10}$

$\equiv 9(5^{33}) \mod{10}$

Note that $\ 5^{33} \equiv 5 \mod{10}$

So $9(5^{33}) \equiv 45 \equiv 5 \mod{10}$

So the answer is $\boxed{5}$ .

$Let~X~and~n ~~be~any~natural~ number.\\ Then~X^n~ is~ odd ~if ~X ~is~ odd,~ and~ even~ if~ X ~is ~even.\\ In~~Given~series~the~terms~alternate~odd~even~odd~ . . .\\ In~ such~ a~series,~if~first~and~last~terms~are~BOTH~of~the~same~type,\\ the~series~will~have~odd~number~of~~odd~~terms.~~\therefore~the~S~is~ODD.\\ 1^{33},~and~89^{33}~both~are~odd, ~so~S~is~odd.~~\implies~ unit~digit~is~odd.\\ If~the~given~list~contains~the~unit~digit~of~S,~its~the~only~odd~digit~\Huge~5.$ .\

take the sum $\mod 90$ we get $45^{33}\mod 90$ Applying CRT with 9 and 10 we get $45 \equiv 0\mod 9$ and $45 \equiv 5 \mod 10$ so that our answer is $45^{33}\mod 90 \equiv 5\mod 90$ .

Using a pattern 1^33: last digit must be 1, 2^33: pattern goes as 2,4,8,6 then back to 2, so 4 numbers per cycle, so 2^33's last digit is 2 3^33: using the same process you get 3 4^33: last digit 4 5^33: Has to be 5 regardless of any positive integer power so it is 5 6^33: same pattern as 5, therefore final digit is 6 7^33: pattern goes as 7,9,3,1,7 so the last is 7 8^33: pattern for last digit goes as 8,4,2,6,8 there the last digit is 8 9^33: pattern is 9,1,9,1, since the power is odd, last digit is 9 Any base that is a multiple of 10 is automatically 0 so these have no effect. Since only the last digit is the same for any base, eg. 1^33, 11^33, 21^33,31^33, etc. all have the same last digit therefore, you add all the last digits which is 45, times by 9 which is 405, and the digit is 5. Voila.

We are looking for $S \mod 10$ . Using the Chinese Remainder Theorem, we will instead consider $S \mod 2$ and $S \mod 5$ and reconstruct the solution. Clearly, $S \equiv 1 \mod 2$ , so consider $S \mod 5$ .

We see that if $5$ divides $a$ , then $a^{33} \equiv 0 \mod 5$ . If $5$ does not divide $a$ , then $a^{33} \equiv a(a^8)^{\phi(5)} \equiv a \mod 5$ . Therefore,

$1^{33}+2^{33}+3^{33}+4^{33}+5^{33}+\ldots +89^{33} \equiv 18(1^{33}+2^{33}+3^{33}+4^{33}) \equiv 3(1+2+3+4) \equiv 0 \mod 5$

The only digit x (integer from $0$ to $9$ ) satisfying $x\equiv 1 \mod 2$ and $x \equiv 0 \mod 5$ is $x=5$ . Thus, $S \equiv 5 \mod 10$ .

The last digit of this sum is the same as that of the sum where we only used the last digits of each of the terms (for example, the $21^{33}$ term serves the same purpose as a $1^{33}$ term, so we can just replace it with that).

Therefore, S has the same last digit as $9\sum_{k=1}^{9}{k^{33}}$ .

For every integer $k$ between 1 and 9 (inclusive), the last digit of $k^5$ is $k$ . Because $k^{33}=(k^{2\cdot5+1})^3=(k^5\cdot k^5\cdot k)^3$ , which has the same last digit (by the factoid just stated) as $(k\cdot k\cdot k)^3=(k^3)^3=k^9=k^5\cdot k^4$ , which has the same last digit as $k\cdot k^4=k^5$ , which has the same last digit as $k$ , our sum S has the same last digit as $9\sum_{k=1}^{9}{k}=9\cdot45$ , which has last digit $\boxed{5}$