Spinning up Sierpinski's carpet

Suppose the carpets moment of inertia about a perpendicular axis through its center is $I = \dfrac a b m \ell^2$ .

The carpet consists of eight copies of the carpet, with mass $m' = m/8$ and length $\ell' = \ell/3$ ; thus each of the eight copies has moment of inertia $I' = \frac a b \frac m 8 \left(\frac \ell 3\right)^2 = \frac I {72}$ about a perpendicular axis through its center .

We must apply the parallel axis theorem to find the moment of inertia of each part about the perpendicular axis through the center of the entire carpet.

For the four parts left, right, above, and below the center, note that the distance between its center and the center of the entire carpet is $\ell/3$ . Thus the moment of inertia of each of these parts is $I_a = I' + m'd^2 = \frac{I}{72} + \frac{m}8\left(\frac\ell 3\right)^2 = \frac{I + m\ell^2}{72}.$ The four parts at the corners have a distance $\tfrac13\sqrt 2\ell$ to the center, contributing $I_b = I' + m'd^2 = \frac{I}{72} + \frac{m}8\left(\frac{\sqrt 2\ell} 3\right)^2 = \frac{I + 2m\ell^2}{72}.$ The total moment of inertia of the eight parts about the central axis of the carpet is therefore $I = 4I_a + 4I_b = \frac1{18}(2I + 3m\ell^2) = \frac19I + \frac16m\ell^2.$ Solving this we get $I = \frac98\cdot\frac16m\ell^2 = \frac 3{16}m\ell^2,$ making our mystery fraction equal to $a/b = 3/16$ , so the answer is $3 + 16 = \boxed{19}$ .

Looking at the Sierpinski carpet, we notice that each of the eight tiles on the periphery is a scaled down replica of the original Sierpinski carpet except with mass $m^\prime = m/8$ and length $\ell^\prime = \ell/3$ . These relationships are sketched out in the figure below.

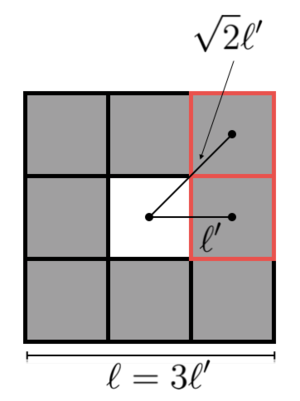
If the moment of inertia of the Sierpinski carpet is $I$ , we expect the moment of inertia of these small tiles about their center of mass to be given by $I_\textrm{8} = I\frac{m^\prime}{m}\left(\frac{\ell^\prime}{\ell}\right)^2=\frac{I}{72}$ .

According to the parallel axis theorem, if an object of mass $m$ has moment of inertia $I$ about an axis through its center of mass, it will have moment of inertia $I^\prime = md^2 + I$ about an axis parallel to the original, a distance $d$ away.

Notice that the subgroup outlined in red is repeated four times around the center of the carpet. Its moment of inertia is given by $I_\textrm{subgroup} = \left(m^\prime {\ell^\prime}^2 + I_\textrm{8}\right) + \left(2m{\ell^\prime}l^2 + I_\textrm{8}\right)$ . Clearly, we have $I = 4I_\textrm{subgroup}$ . Expressing $I_\textrm{subgroup}$ in terms of $I$ , we obtain a self-consistent equation for $I$ : $\begin{aligned} I &= 4I_\textrm{subgroup} \\ &= 4\left(m^\prime {\ell^\prime}^2 + I_\textrm{8}\right) + 4\left(2m^\prime{\ell^\prime}^2 + I_\textrm{8}\right) \\ &= 4\left(\frac{m}{8}\frac{\ell^2}{9} + \frac{m}{4}\frac{\ell^2}{9} + 2I_\textrm{8}\right) \\ &= 4\left(\frac{1}{24}m\ell^2 + \frac{I}{36}\right) \end{aligned}$

Solving this equation, we find $\boxed{I = \frac{3}{16}m\ell^2}$ .

Postscript

Note the Sierpinski carpet has zero area, so the idea of calculating its moment of inertia is something of a dubious proposition. The sleight of hand that makes it all work is to assume that the whole carpet has a non-zero moment of inertia to begin with. What this implies is that the infinitely thin lines that remain after all the subdividing has occurred are made up of Dirac point particles. In other words, a collection of points whose mass density is nonzero only in infinitesimally small regions. Moreover, it is nonzero in such a way that it contributes nonzero-mass. Take some time to think about this point.