Monkey's Typing Challenge

In a random string of letters, the words $\text{HEART}$ and $\text{EARTH}$ have equal probabilities, but $\text{HEART}$ is more likely to appear nearer to the beginning of the string.

The two words in question share the substring $\text{EART}.$ Imagine searching through a random string and finding the first instance of $\text{EART}.$ In the context of this question, we care about three scenarios:

1. $\text{EART}$ is preceded by $\text{H}$ to form $\text{HEART}$
2. $\text{EART}$ is followed by $\text{H},$ and is not preceded by $\text{H},$ to form $\text{EARTH}$
3. $\text{EART}$ is neither preceded nor followed by $\text{H},$ in which case we move on and look for the next instance of $\text{EART}.$

The probability of scenario 1. is $\frac{1}{26} \approx 0.0385$ since the letters are selected independently. Notice that it doesn't matter if $\text{EART}$ is followed by $\text{H}$ here because $\text{HEART}+\text{H}$ would still count as $\text{HEART}$ appearing first.

Similarly in scenario 2., the probability that $\text{EART}$ is followed by $\text{H}$ is $\frac{1}{26}$ since the letters are selected independently. But the letter preceding $\text{EART}$ cannot be $\text{H},$ or it would count as $\text{HEART}$ appearing first. The probability that the preceding letter is not $\text{H}$ is $\frac{25}{26},$ so the joint probability is $\frac{1}{26} \times \frac{25}{26} \approx 0.0370.$

We can see that each instance of substring $\text{EART}$ has a $0.385\%$ chance of forming the word $\text{HEART},$ but only a $0.370\%$ chance of forming the word $\text{EARTH}$ and not the word $\text{HEART}.$ Thus, $\text{HEART}$ is slightly favored to appear first in a random string.

Intuition

On first read this might seem like a trick question.

Suppose we go to position $i$ in any string $S$ prepared with the method described in the problem. There is, of course, an equal probability for the string $S_{i:(i+4)}$ to be $\textrm{EARTH}$ or $\textrm{HEART},$ equal to $1/26^5.$

But what is the probability for it to be $\textrm{EARTH}$ or $\textrm{HEART}$ given that neither $\textrm{EARTH}$ nor $\textrm{HEART}$ have appeared yet?

Suppose we want to know the probability of the string starting at position $i$ being $\textrm{EARTH}$ AND that it is the first time that either $\textrm{EARTH}$ or $\textrm{HEART}$ appear in the string. What we need to worry about is the following: if $S_{i:(i+4)}$ is to be the first appearance of $\textrm{EARTH},$ then $S_{(i-1)}$ cannot be $\textrm{H}$ or else we'd have $S_0S_1\cdots S_{i-2}\textrm{HEARTH}$ and $\textrm{HEART}$ would slide into the win just as $\textrm{EARTH}$ was to appear.

Similarly, if it is to be $\textrm{HEART}$ AND the first time that either $\textrm{HEART}$ or $\textrm{EARTH}$ appear in the string, then the substring $S_{(i-4):(i-1)}$ cannot be $\textrm{EART}.$

From here, it's already clear that we're less likely to have $S_{(i-4):(i-1)} = \textrm{EART}$ than we are to have $S_{(i-1)}=\textrm{H},$ so $\textrm{HEART}$ is more likely to appear first. But to get quantitative, we have to do a calculation.

Calculation

We can write these probabilities as

$P\left(\textrm{EARTH} = S_{i:(i+4)}\ \mathbf{AND}\ \textrm{H} \neq S_{(i-1)} \biggr\rvert\{\textrm{EARTH},\textrm{HEART}\}\notin S_{0:(i-1)}\right)$

and the corresponding one for $\textrm{HEART}$ as

$P\left(\textrm{HEART} = S_{i:(i+4)}\ \mathbf{AND}\ \textrm{EART} \neq S_{(i-4):(i-1)}\biggr\rvert\{\textrm{EARTH},\textrm{HEART}\}\notin S_{0:(i-1)}\right)$

Note that both of these probabilities are conditioned upon neither $\textrm{EARTH}$ nor $\textrm{HEART}$ appearing in $S_{0:(i-1)},$ so we don't have to worry about the likelihood of those events occurring. For simplicity, we'll write the first expression above as $P_i\left(\textrm{EARTH}\right)$ from here on, and likewise for the $\textrm{HEART}$ probability.

For the first expression above we need $S_{(i-1)}\neq\textrm{H},$ $S_{i:(i+3)} = \textrm{EART},$ and $S_{(i+4)}=\textrm{H}.$ Thus,

$P_i\left(\textrm{EARTH}\right) = P(S_{(i-1)}\neq\textrm{H})\times P\left(\textrm{EART}\right)\times P\left(\textrm{H}\right)$ and likewise $P_i\left(\textrm{HEART}\right) = P(S_{(i-4):(i-1)}\neq\textrm{EART})\times P\left(\textrm{H}\right)\times P\left(\textrm{EART}\right)$

Thus, the probability that $\textrm{HEART}$ appears in $S$ before $\textrm{EARTH}$ is given by

$\begin{aligned} P(\textrm{HEART before EARTH}) &= \frac{P_i\left(\textrm{HEART}\right)}{P_i\left(\textrm{HEART}\right) + P_i\left(\textrm{EARTH}\right)} \\ &= \frac{P(S_{(i-4):(i-1)}\neq\textrm{EART})\times P\left(\textrm{H}\right)\times P\left(\textrm{EART}\right)}{P(S_{(i-4):(i-1)}\neq\textrm{EART})\times P\left(\textrm{H}\right)\times P\left(\textrm{EART}\right) + P(S_{(i-1)}\neq\textrm{H})\times P\left(\textrm{EART}\right)\times P\left(\textrm{H}\right)} \\ &= \frac{P(S_{(i-4):(i-1)}\neq\textrm{EART})}{P(S_{(i-1)}\neq\textrm{H}) + P(S_{(i-4):(i-1)}\neq\textrm{EART})} \end{aligned}$

After the cancellations, the probabilities we're left with are simple. If the size of our alphabet is $A,$ then $\begin{aligned} P(S_{(i-1)}\neq\textrm{H}) &= 1-A^{-1} \\ P(S_{(i-4):(i-1)}\neq\textrm{EART}) &= 1 - A^{-4} \end{aligned}$ and $\boxed{\displaystyle P(\textrm{HEART before EARTH}) = \frac{1 - A^{-4}}{2 - A^{-1} - A^{-4}}}.$

Estimate

For the 26 letter alphabet, $A^{-4}$ is very small compared to $A^{-1},$ so we can neglect $A^{-4}$ and expand in $A^{-1}$ as follows $\begin{aligned} P(\textrm{HEART before EARTH}) &\approx \frac12\left(1 + \frac{1}{2A}\right) \\ &= \frac12 + \frac{1}{4A} \\ &\approx 0.5096\ldots \end{aligned}$

The exact probability is approximately $\num{0.50980337470366754985}.$

Generalization

We can generalize this to the case of alphabets of size $A\geq N$ where $N$ is the length of the two words. In our specific case $A$ was 26 and $N$ was 5. For general $A$ and $N,$ we have

$P(N,A) = \frac{1-A^{-(N-1)}}{2 - A^{-1} - A^{-(N-1)}}.$

Simulation

Given how surprising the result is, it is reassuring to verify it by explicitly performing the suggested typing exercise.

Below are the results when we run the experiment on small alphabets of size $A$ equal to the length of the two words. E.g. for $A=4$ , we check whether $\textrm{DABC}$ or $\textrm{ABCD}$ appears first when we enumerate random strings from the alphabet $\{\textrm{A}, \textrm{B}, \textrm{C}, \textrm{D}\}.$

Simulation results for $N=\num{200000}$ random typing experiments.

There seems to be close agreement between our prediction and the simulation.

For reference, the code is below. You can also add letters not in either of the competing words by uncommenting/adding to the list extra .

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

import string
import random

string1 = "ABCDEF"
string2 = "FABCDE"

letters = list(string1) 
extra = list("MNOP")
alphabet = letters #+ extra

counts = {"ONE": 0, "TWO": 0}

def measure():

    my_string = "0" * len(string1)
    over = None

    while over is None:
        my_string = my_string[1:] + random.choice(alphabet)
        if my_string == string1:
            over = "ONE"
        elif my_string == string2:
            over = "TWO"
    return over

for round in range(200000):
    counts[measure()] += 1

print(counts)

In a string of indefinite length, consider all instances of the sub-string "EART" Let Z be any letter that is not H. Then we can have sub-strings ZEARTZ, HEARTZ, HEARTH, ZEARTH that can occur.

If HEARTZ is equally likely as ZEARTH to first occur, then because of some chance that HEARTH can be the first to occur, then HEART is more likely to be the first to occur.

Now that Josh Silverman has posted his full solution with the computed probability, let's look at the probability of just one H appearing either at front or back of EART, and the probability of appearing both

$A=\dfrac{1}{26} \dfrac{25}{26}$
$B=\dfrac{1}{26} \dfrac{1}{26}$

Hence, the probability of HEART appearing first should be

$\dfrac{A+B}{2A+B}=0.509804...$

which almost agrees with Josh's figure. Right now I"m not ready to say that my figure here is correct.

Edit: Josh's figure is the accurate one. The solution provide here is still only an approximation, as it does not distinguish between the two cases in that small chance of EART appears in the first few letters of the sequence. My solution neglects the small chance that the sequence begins with EART. Both figures agree to six decimal places, and then diverges.

We can think of this process as an automaton, with the following states and transitions: 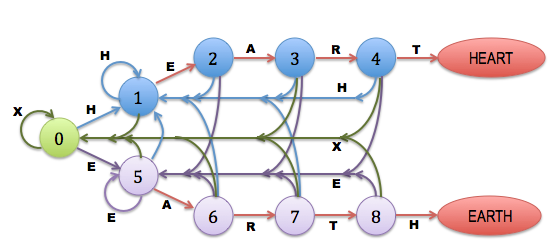(blue line: H; purple line: E; green line: other letter (X))

$\begin{array}{r|cccccc} \text{state} & H & E & A & R & T & \text{other} \\ \hline \text{start:}\ 0 & 1 & 5 & 0 & 0 & 0 & 0 \\ 1 & 1 & 2 & 0 & 0 & 0 & 0 \\ 2 & 1 & 5 & 3 & 0 & 0 & 0 \\ 3 & 1 & 5 & 0 & 4 & 0 & 0 \\ 4 & 1 & 5 & 0 & 0 & \mathbf{HEART} & 0 \\ 5 & 1 & 5 & 6 & 0 & 0 & 0 \\ 6 & 1 & 5 & 0 & 7 & 0 & 0 \\ 7 & 1 & 5 & 0 & 0 & 8 & 0 \\ 8 & \mathbf{xEARTH} & 5 & 0 & 0 & 0 & 0 \\ \hline \end{array}$

Let $P(s)$ indicate the probability that a state $s$ will eventually lead to the finals state $\mathbf{HEART}$ . The probability of $\mathbf{xEARTH}$ is then $1 - P(s)$ . Treating $P(\cdot)$ as a vector, we may write the transition probabilities as follows, where $\alpha = \tfrac1{26}$ is the probability of an individual letter: $\mathbf P(s) = \left[\begin{array}{ccccccccc} 1 - 2\alpha & \alpha & & & & \alpha & & & \\ 1 - 2\alpha & \alpha & \alpha & & & & & & \\ 1 - 3\alpha & \alpha & & \alpha & & \alpha & & & \\ 1 - 3\alpha & \alpha & & & \alpha & \alpha & & & \\ 1 - 3\alpha & \alpha & & & & \alpha & & & \\ 1 - 3\alpha & \alpha & & & & \alpha & \alpha & & \\ 1 - 3\alpha & \alpha & & & & \alpha & & \alpha & \\ 1 - 3\alpha & \alpha & & & & \alpha & & & \alpha \\ 1 - 2\alpha & & & & & \alpha & & & \end{array}\right]\ \mathbf P(s) + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \alpha \\ 0 \\ 0 \\ 0 \\ 0\end{array}\right].$ This can be reduced to $\left[\begin{array}{ccccccccc} -2\alpha & \alpha & & & & \alpha & & & \\ 1 - 2\alpha & \alpha-1 & \alpha & & & & & & \\ 1 - 3\alpha & \alpha & -1 & \alpha & & \alpha & & & \\ 1 - 3\alpha & \alpha & & -1 & \alpha & \alpha & & & \\ 1 - 3\alpha & \alpha & & & -1 & \alpha & & & \\ 1 - 3\alpha & \alpha & & & & \alpha-1 & \alpha & & \\ 1 - 3\alpha & \alpha & & & & \alpha & -1 & \alpha & \\ 1 - 3\alpha & \alpha & & & & \alpha & & -1 & \alpha \\ 1 - 2\alpha & & & & & \alpha & & & -1 \end{array}\right]\ \mathbf P(s) = \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ -\alpha \\ 0 \\ 0 \\ 0 \\ 0\end{array}\right].$

Lazily, I solved this numerically and found $\mathbf P(s) = \left[\begin{array}{c} 0.509803 \\ 0.509804 \\ 0.509831 \\ 0.510529 \\ 0.528657 \\ 0.509802 \\ 0.509774 \\ 0.509049 \\ 0.490196 \end{array}\right].$ Specifically, $P(S) = 0.509803 > \tfrac12$ , so that the final state $\mathbf{HEART}$ is more likely than $\mathbf{xEARTH}$ .

Note that this is true at any point during the process, except in state $8$ : at that point, the outcome $\mathbf{xEARTH}$ is slightly more probable.

No need for a bunch of math here. On average the letters EART will show up after some expected number of letters are chosen. The probability that an H will be in front of the E is the same as the probability that an H will be behind the T, but when both the letter before the E and after the T are H, HEART wins. This means there are more ways for for HEART to win than for EARTH to win.

If we ignore the possibility of EARTH appearing as the first characters (1 in 11,881,375) this is analogous to two people taking turns flipping a coin and the winner being the first to land heads. The person who goes first has a clear advantage: 1/2 + 1/8 + 1/32... versus 1/4 + 1/16 + 1/64...

In this case the aim is to type an H first, and the Heart team goes first, so has the advantage.

The occurrence of EART can be ignored, it is simply the trigger for each turn, but the probabilities would be the same without it —the game would just be a lot quicker.