More fun in 2015, Part 28
5 x 2 + 6 y 2 + 7 z 2 = 4 x y + 4 y z + 2 0 1 5
Let M and m be the maximum and the minimum of x 2 + y 2 + z 2 subject to the constraint above, where x , y and z are real numbers. Find m M .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You're missing a lot of crucial parts. I'm already lost in your very first line.
Log in to reply
As I told you earlier, my work is based on eigenvalues, but I wrote my solution without explicit reference to them, which makes it a bit mysterious. The solution is very systematic and straightforward, however.
The matrix of the quadratic form 5 x 2 + 6 y 2 + 7 z 2 − 4 x y − 4 y z is ⎣ ⎡ 5 − 2 0 − 2 6 − 2 0 − 2 7 ⎦ ⎤ We "split" the mixed terms − 4 x y and − 4 y z off the diagonal to make the matrix symmetric. The eigenvalues are 3, 6, and 9, and the answer to our problem is the ratio of the extreme eigenvalues, 9 and 3.
Here is another problem that you could solve quickly this way, without resorting to these weird inequalities that seem so forced and arbitrary.
Log in to reply
Thanks. You should put that in your solution.
Question 1 : What is the reasoning behind
min max = ratio of extremes of eigenvectors ?
Question 2 : How do you form a matrix such that their eigenvectors are "nice numbers"? Or you must (and is the only way) go through det ( A − λ I n ) = 0 ?
Log in to reply
@Pi Han Goh – You ask interesting questions, as usual.
I have another busy day of work ahead of me, so, let me (try to) answer Question 2 for now. As a linear algebra teacher, I'm often faced with the problem of constructing a nice matrix A (with integer entries, say) with given (integer) eigenvalues. It's pretty easy: Just make A = S − 1 D S , where D is diagonal with the desired eigenvalues on the diagonal, and S is an integer matrix with determinant 1 or -1 (that guarantees that the inverse has integer entries). One way to construct such matrices S is to start with a triangular matrix with 1's and -1's on the diagonal, and then add multiples of rows (or columns) to other rows (or columns) to "mix things up".
I hope to get to Question 1 later. In the meantime, I posted another problem addressing this issue.
Log in to reply
Help please. I'm not getting a symmetric matrix!
Log in to reply
@Pi Han Goh – You asked "How do you form a matrix such that their eigenvectors are "nice numbers"? "... You did not ask for a symmetric matrix and I did not give you one, Comrade. ;) I have some special tricks for those that I will gladly share when I have a little free time.
To get a more interesting (non-symmetric) matrix with eigenvalues 2,6,7 you could do ⎣ ⎡ 1 2 3 1 3 6 1 4 1 0 ⎦ ⎤ − 1 ⎣ ⎡ 2 0 0 4 6 0 5 6 7 ⎦ ⎤ ⎣ ⎡ 1 2 3 1 3 6 1 4 1 0 ⎦ ⎤ = ⎣ ⎡ 5 1 − 3 2 6 9 0 − 5 8 1 2 1 4 2 − 9 6 2 2 ⎦ ⎤
Log in to reply
@Otto Bretscher – .
I have some special tricks for those that I will gladly share when I have a little free time.
Please share your wisdom! Comrade Otto =D
@Otto Bretscher – Can you write up a full solution for any of the practice problems here so I can replicate the result?
@Otto Bretscher – But how do you make it symmetric? (So I can convert it to a quadratic form)
Log in to reply
@Pi Han Goh – I love to share some of my techniques with a Comrade ;)
One simple technique is to use A = S − 1 D S where D is diagonal and S is orthogonal with rational entries... you can then scale A to make the entries integers.
Matrices that I often use for S are variants of [ 0 . 6 0 . 8 − 0 . 8 0 . 6 ] , 3 1 ⎣ ⎡ 2 − 2 − 1 2 1 2 1 2 − 2 ⎦ ⎤ , 2 1 ⎣ ⎢ ⎢ ⎡ 1 1 1 1 1 1 − 1 − 1 1 − 1 − 1 1 1 − 1 1 − 1 ⎦ ⎥ ⎥ ⎤
For example, if you take D = [ 4 0 0 9 ] and the S above you get A = S − 1 D S = [ 7 . 2 2 . 4 2 . 4 5 . 8 ] ... multiply by 5 if you want an integer example. That's how I constructed this problem ...
I'm giving away my "secrets" here (for Comrades only!) ;) many of my recent problems are based on this construction.
Log in to reply
@Otto Bretscher – Can you give an explicit example? I'm new to this. Thank you Comrade Otto =D
@Pi Han Goh – Here are a few remarks to Question 1, brief as usual... that is all you need.
The question boils down to finding the maximum and minimum of q ( x ) = x T A x , where A is a symmetric matrix and x is a unit vector. By the Spectral Theorem, there exist perpendicular unit eigenvectors u , v , w . with corresponding eigenvalues a ≤ b ≤ c . Now q ( w ) = c is the maximum, etc.
Can u post a simple solution that a rookie can understand. Sorry for the pain 😆
Log in to reply
Do you like Lagrange multipliers? All that is required are partial derivatives...
Log in to reply
I have never heard of it. Please can u explain or attack a link for the following. Thanks
Log in to reply
@Neelesh Vij – You may benefit from reading Brian's excellent solution here
So how do we know what type of surface this is without finding its eigenvalues (by completing the squares alone)? I have some feeble attempts but all boils down to randomly factoring terms after this step:
5 x 2 + 6 y 2 + 7 z 2 − 4 x y − 4 y z = 2 0 1 5 .
Note : I'm asking for a systematic approach, not some random "Oh I factorized it nicely by accident!" approach.
And yes, I know there are 3 positive eigenvalues, which implies that it is an ellipsoid.
Log in to reply
Yes, completing the squares is a very systematic process, although it can get a bit messy if done by hand. You start with the terms involving x , in our case 5 x 2 − 4 x y = 5 ( x 2 − 5 4 x y ) = 5 ( x − 5 2 y ) 2 − 5 4 y 2 . Now you take care of the terms involving y , and you are done.
Log in to reply
ohhhhhhhhhhhhhhhh this is simpler than I thought!!! I was working on completing all 3 squares at the same time!
Here's the answer:
5 x 2 + 6 y 2 + 7 z 2 − 4 x y − 4 y z = = = = = = = 5 ( x 2 − 5 4 x y ) + 6 y 2 + 7 z 2 − 4 y z 5 ( ( x − 5 2 y ) 2 − 2 5 4 y 2 ) + 6 y 2 + 7 z 2 − 4 y z 5 ( x − 5 2 y ) 2 + y 2 ( 6 − 5 4 ) + 7 z 2 − 4 y z 5 ( x − 5 2 y ) 2 + 5 . 2 y 2 − 4 y z + 7 z 2 5 ( x − 5 2 y ) 2 + 5 . 2 ( y 2 − 5 . 2 4 y z ) + 7 z 2 5 ( x − 5 2 y ) 2 + 5 . 2 ( ( y − 5 . 2 2 z ) 2 − 5 . 2 2 4 z 2 ) + 7 z 2 5 ( x − 5 2 y ) 2 + 5 . 2 ( y − 5 . 2 2 z ) 2 + z 2 ( 7 − 5 . 2 4 )
Since 5 , 5 . 2 , 7 − 5 . 2 4 are all positive numbers, then the surface is an ellipsoid.
Log in to reply
@Pi Han Goh – Yes exactly! You can type much faster than me ;)
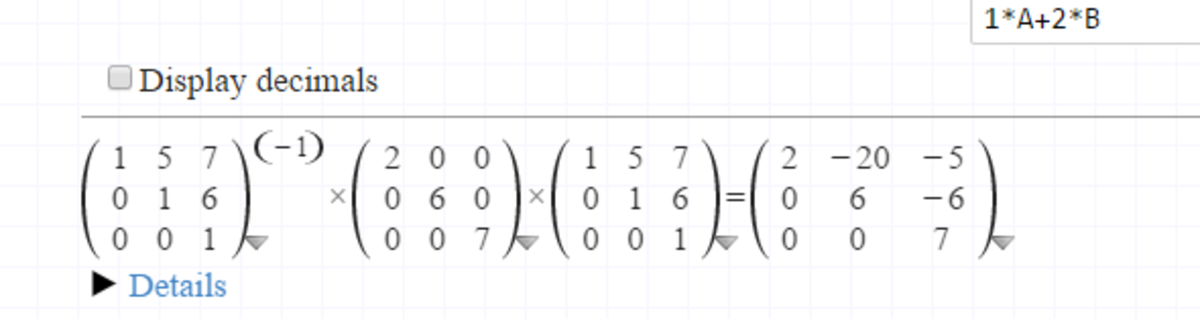
Make a substitution x = ( u − 2 v + 2 w ) / 3 , y = ( − 2 u + v + 2 w ) / 3 , z = ( 2 u + 2 v + w ) / 3 . Now we are asked to find the extrema of u 2 + v 2 + w 2 subject to the constraint u 2 + 2 v 2 + 3 w 2 = 2 0 1 5 / 3 . We have m = 2 0 1 5 / 9 = ( u 2 + 2 v 2 + 3 w 2 ) / 3 ≤ u 2 + v 2 + w 2 ≤ u 2 + 2 v 2 + 3 w 2 = 2 0 1 5 / 3 = M , so that M / m = 3