More fun in 2016, Part 4
Find the largest integer n such that n , n + 2 0 1 6 , and n − 2 0 1 6 are all perfect squares.
Enter 666 if you come to the conclusion that no such n exists.
Bonus Question (very hard) : Does there exist a rational number q such that q , q + 2 0 1 5 and q − 2 0 1 5 are all squares of rational numbers?
The answer is 4225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thanks for a clear and systematic solution! (+1). It turns out that 4225 is the only solution.
Log in to reply
How will one find then number of pairs (not explained in the solution).
Log in to reply
As Aareyan explains well, we need to think about the positive integer solutions of the equation a 2 − b 2 = 2 0 1 6 . Since a + b and a − b must be divisors of 2016, we can find the pairs ( a , b ) by systematically going through all the divisors of 2016. I think we end up with 12 pairs of positive integers. (There are short-cuts.)
Log in to reply
@Otto Bretscher – Actually I am asking for short-cuts.
Log in to reply
@Department 8 – 2 0 1 6 = 2 5 ∗ 3 2 ∗ 7 solutions(positive ints)= when both s+k and s-k are either even or odd(not possible here). =all divisors - odd divisors - the divisors with factor 2 5 .=(5+1)(2+1)(1+1)-(2+1)(1+1)-(2+1)(1+1)=24. i get 24, and wolfram is telling total to be 48(as negative included). so i think i am right here
Log in to reply
@Aareyan Manzoor – Your count is off by a factor of 2, Aareyan, since we want s + k > s − k as we are counting positive solutions only. Luckily, we need to consider only 12 cases.
Log in to reply
@Otto Bretscher – oops, sir. i should have noticed that. thanks, will come in handy in future,
Yes Same Method, Nice Problem.
This is an example of the Congruum Problem discussed and solved by Fibonacci in his book "Liber Quadratorum" of 1225.
What follows is merely an outline of a solution.
The problem is closely related to Pythagorean triples. Indeed, if we have a triple a 2 = b 2 + c 2 with b c = 1 0 0 8 , then a 2 ± 2 b c = a 2 ± 2 0 1 6 = ( b ± c ) 2 , so that n = a 2 solves our problem.
To find a triple a 2 = b 2 + c 2 with b c = 1 0 0 8 , we use Euclid's formula and write b = 2 p q and c = p 2 − q 2 . From the condition b c = 1 0 0 8 we quickly find that p = 8 , q = 1 , b = 1 6 , c = 6 3 and n = a 2 = b 2 + c 2 = 4 2 2 5
We can also figure out that the last digit of the number of which n is square must be 5. Now its easy to check with calculator in hand that 65 is the solution
Not a good solution at all
Let ⎩ ⎪ ⎨ ⎪ ⎧ n = k 2 n + 2 0 1 6 = s 2 n − 2 0 1 6 = t 2 . so we find that s 2 − k 2 = 2 0 1 6 ⟹ ( s − k ) ( s + k ) = 2 0 1 6 k 2 − t 2 = 2 0 1 6 ⟹ ( k − t ) ( k + t ) = 2 0 1 6 We see that s − k and s + k are both factors of 2016. Similarly for k − t and k + t . This gives us a simultaneous system of equations for which we're looking for integer solutions. If we let the solutions to a 2 − b 2 = 2 0 1 6 be ( a 1 , b 1 ) , ( a 2 , b 2 ) . . . , then we must have s as an a i and t as a b i . However, k must also be both an a i and a b i . We find all pairs in a decreasing order and stop once we find the potential k .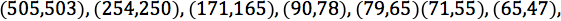 We check and see that
k
=
6
5
satisfies the equation and is indeed the biggest possible
k
. The answer is hence
n
=
k
2
=
4
2
2
5
We check and see that
k
=
6
5
satisfies the equation and is indeed the biggest possible
k
. The answer is hence
n
=
k
2
=
4
2
2
5