More Fun With Power Towers
a a a ⋅ ⋅ ⋅ = b
Find the largest real number b such that the above equation has a positive real solution a . Approximate b to four significant digits.
If you come to the conclusion that no such value of b exists, enter 666.
Clarification : The value of the infinite power tower a a a ⋅ ⋅ ⋅ is defined as the limit of the sequence x 0 = a , x n + 1 = a x n .
The answer is 2.718.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The first time I ever saw this problem (a few years ago), I fell into the trap of thinking, "Oh, it's just x y = y , and ( n n ) n = n , so there is no upper bound!"
Log in to reply
You are not alone... it looks like 152 people fell into that trap here . BTW: That wrong answer should really be changed... it seems to confuse people further.
I'm following you up to last sentence, but I don't quite see how you conclude that there exists an a as required for b = e .
Log in to reply
I only show that the supremum (as opposed to the maximum) of the limit b is e , i.e. anything less than e is achievavble.
Log in to reply
But the problem asks for the largest b that is achievable.
To complete the proof, let us show that e = a a a . . . for a = e 1 / e ; this proof goes back to Euler. Now the line y = x is tangent to the graph of f ( x ) = a x = e x / e at the point ( e , e ) ; to verify this, note that f ( e ) = e and f ′ ( e ) = 1 . The sequence given by x 0 = a and x n + 1 = a x n = f ( x n ) is increasing and bounded by e , so that it must converge to e as claimed.
If a > e 1 / e , then the function f ( x ) = a x will no longer have an equilibrium point where f ( x ) = x , so that the power tower a a a . . . fails to converge. Thus b = e is the largest "achievable" value.
To SEE what's going on here, take a look at Mr @Michael Mendrin 's last graph and draw a cobweb starting at a = e 1 / e ≈ 1 . 4 4 ... the cobweb will zigzag towards the point ( e , e )
e
is where
y
y
1
has the maximum value. See graphic.
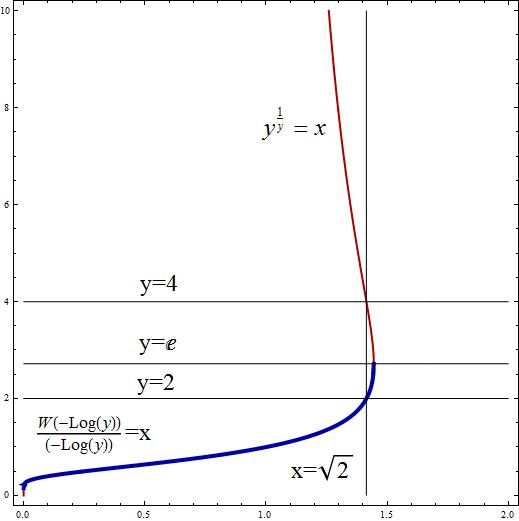
Note that d y d ( y y 1 ) = y y 1 − 2 ( 1 − L o g ( y ) )
That is certainly true... but how does this relate to our problem? I know that you are fond of brief solutions (as am I), but I think we need to say just a little more.
Log in to reply
Here's how it's related
y = x x x . . . = x y
which leads to the inverse function of the power tower y y 1 , and so we plot it in the other way, and see that it arcs back after reaching the maximum value of e
Log in to reply
But we also need to worry about convergence: For a given b , does the power tower with a = b 1 / b actually converge to b ?
Log in to reply
@Otto Bretscher – Ten Spaces
Edit: Ten spaces is what's required for Brilliant.org to "finish a post". I'll be back with a graphic after I've had my pizza.
Okay, first let's look at this graphic
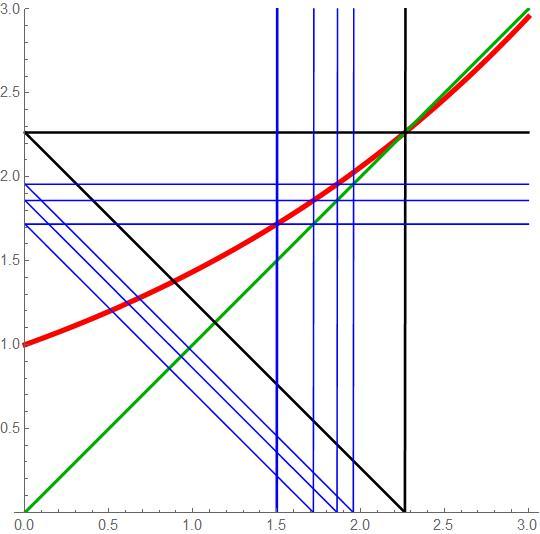
The red curve is the function y = a x . The green line is y = x . Starting at an arbitrary x = a (thick vertical blue), we reiterate (follow the blue lines), which effectively "builds the tower". This iteration finally ends at the black lines where a x = x . The variable a can only be increased until the line y = x is tangent to a x like as per this graphic
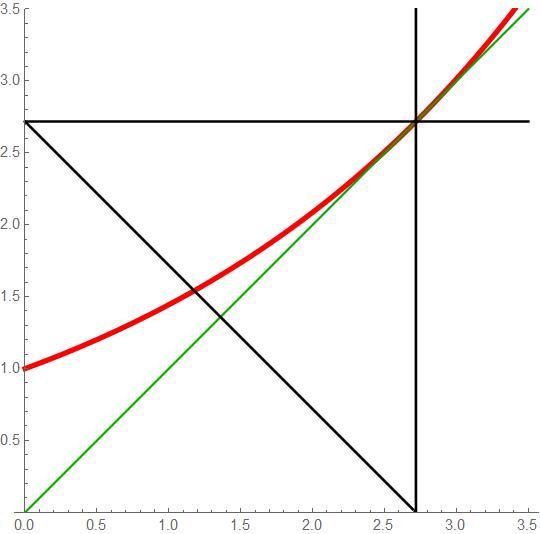
which means that the slope at the critical point is 1 , or
d x d a x = a x L o g ( a ) = 1
but we know that a = x x 1 , so that we end up with
( x x 1 ) x L o g ( x x 1 ) = 1
and from here it's a short step to showing that x = e , which is the answer.
Log in to reply
@Michael Mendrin – bon appetit
@Michael Mendrin – Yes, that makes sense! Thanks!
If a a a . . . = b
then − ln a W ( − ln a ) = b
by identity, W ( − ln a ) e W ( − ln a ) W ( − ln a ) = b
e W ( − ln a ) 1 = b
e − W ( − ln a ) = b
W ( − ln a ) = − ln b
− ln a = − ln b e − ln b
ln a = b ln b
So, a = b b
We want a to the maximum so b b has to be maximum; and for a function to be maximum (or minimum), its derivative has to be 0. The derivative of b b is − b b 1 − 2 ( ln b − 1 )
So, − b b 1 − 2 ( ln b − 1 ) = 0
that means either − b b 1 − 2 = 0 or ln b − 1 = 0
The first one is not possible, even if b is 0, so
If ln b − 1 = 0
then ln b = 1
thus b = e
Thus the maximum is e
You need to show that e = a a a . . . for a = e 1 / e . You only show "necessity", not sufficiency, to use Abhishek's terminology.
Log in to reply
why not proof by induction?
Log in to reply
Euler's proof (written up in my comment to Abhishek's partial solution) is indeed by induction: If x n < e then x n + 1 < e .
Log in to reply
@Otto Bretscher – if not 2 . 7 2 . 7 1 ≈ 1 . 4 4 4 6 5 6 and 2 . 8 2 . 8 1 ≈ 1 . 4 4 4 4 3 9
thus 2 . 7 2 . 7 1 > 2 . 8 2 . 8 1 ????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Log in to reply
@Joel Yip – As I said before: The key point of this problem is to show that e = a a a . . . for a = e 1 / e ; we need to prove that the power tower converges to e . The rest is trivial
Log in to reply
@Otto Bretscher – then i'll try.
− ln e e 1 W ( − ln e e 1 )
− ln e e 1 W ( − e 1 )
− ln e e 1 − 1
− e 1 − 1
and that is e
Log in to reply
@Joel Yip – That only shows that e is a fixed point... but you have to show that the sequence defined by the power tower converges to e .
Log in to reply
@Otto Bretscher – sir why is that necessary when you are showing it converges to e?and i dont understand how @Michael Mendrin shows that the sequence converges to e? pls clarify
Log in to reply
@Mardokay Mosazghi – Mr @Michael Mendrin shows it graphically: In his last graph, you can draw a cobweb between the green line y = x and the red graph of y = a x , where a = e 1 / e ... this cobweb zigzags towards the point ( e , e ) . The cobweb is a neat way to visualize the iteration.
Log in to reply
@Otto Bretscher – thx i wasn't aware of the cobweb representation, anyways how would you show the convergence with out a graphical approach any tips?
Log in to reply
@Mardokay Mosazghi – I'm showing it as a comment to Abhishek's solution... it's an old proof due to Euler. Abhishek shows the convergence for b < e , but not for e itself.
[Necessity] Fix a number a > 1 . Let us first characterize a necessary condition for the number a , so that the limit a a ⋅ ⋅ ⋅ exists in R .
If the limit does exist, then there must exist a real number x , such that the following equation has a real solution a x = x Now, consider minimizing the convex function f ( x ) = a x − x , x ∈ R . At the minima x ∗ , the first derivative must vanish, thus we must have a x ∗ ln ( a ) = 1 Hence, x ∗ = − ln ( a ) ln ( ln ( a ) ) Hence the minimum value of f ( x ) is a x ∗ − x ∗ = ln ( a ) 1 + ln ( ln ( a ) ) . For the equation a x = x to have a real solution, this minimum value must be non-positive. Thus, the limit above does not exist if 1 + ln ( ln ( a ) ) > 0 i.e., a > e 1 / e Hence, for the limit to exist, we must have a ≤ e 1 / e .
[Sufficiency] Now, we show that for any 1 < b < e , the mapping g : [ 1 , b ] → [ 1 , b ] , given by g ( x ) = b x / b , is a well-defined contraction mapping. This can be directly verified by taking derivative of g ( x ) and showing that it is strictly less than unity in the compact interval [ 1 , b ] .
Taking a = b 1 / b , it follows by Banach's fixed point theorem , that the iteration g m ( a ) = a g m − 1 ( a ) converges, since the point a belongs to the domain (i.e., 1 ≤ a = b 1 / b ≤ b ). Thus the supremum of all numbers a for which the limit exists is e 1 / e with the corresponding supremum value of the limit being e .