More poison chocolate

Whatever Charlie's first move, Tracy can place the coin on one of the orange squares.

Then note that landing on the green square is a bad idea, as you then have the next move. Whatever you then do, your opponent can put it either on the blue square, or one of the purple squares, which makes them win (as seen in the first problem since only either successive lefts or successive ups are allowed).

This means that Charlie must place the coin on one of the white squares which can be reached from whichever orange square it is currently at. However, Tracy can then move it to one of the purple squares, forcing a win for Tracy.

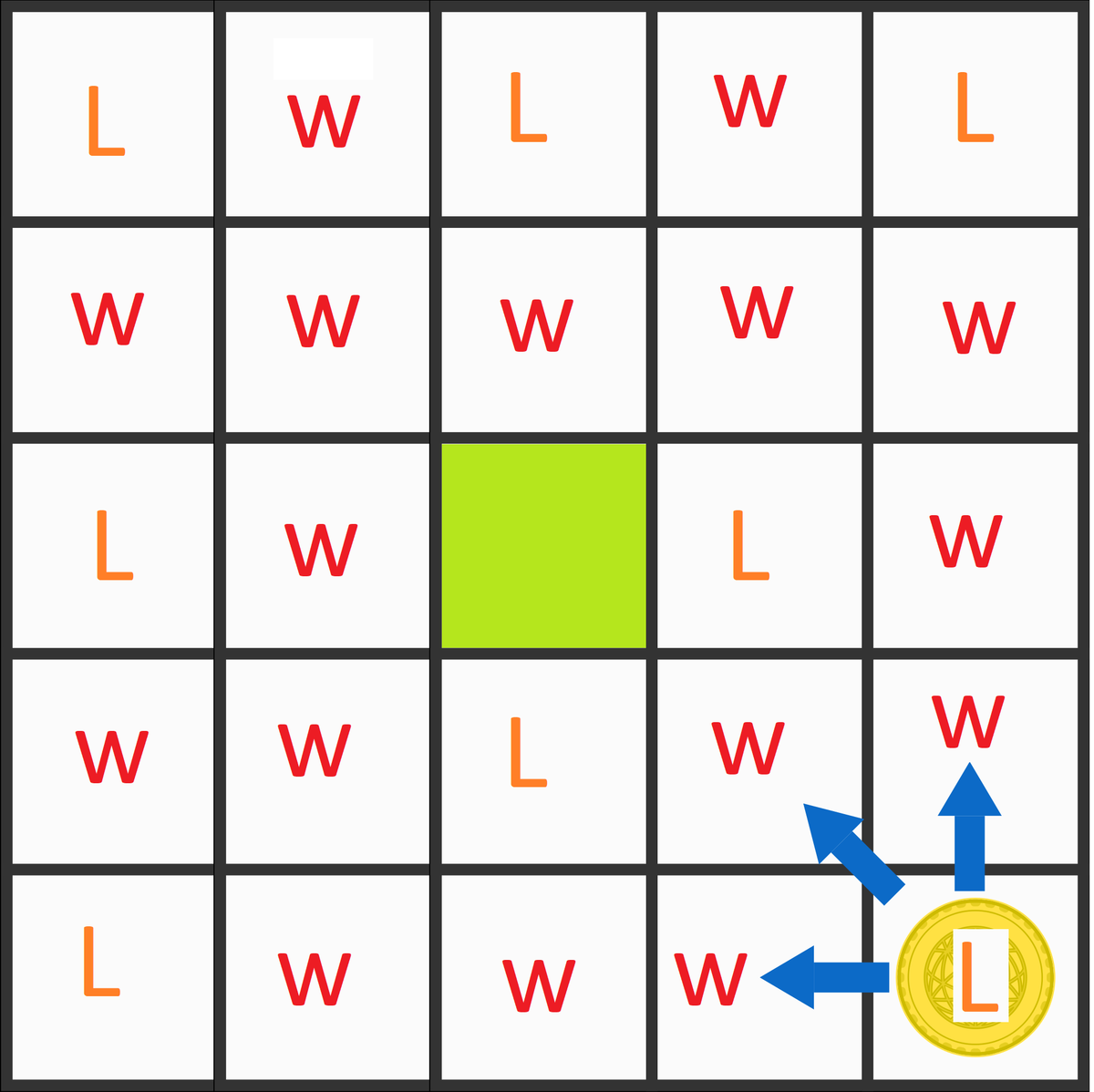
The green square doesn't help. It was a losing position before, so using it is still a losing move.

The Sprague-Grundy function for this game can be shown graphically as

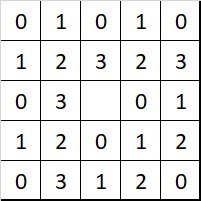
with the squares marked $0$ being losing squares to start on. The SG value of each board position is the mex of the board positions that can be reached from that starting position ("mex" is short for minimum-excluded , so the SG value of a board position is the smallest nonnegative integer that is not on any of the board positions reachable from that position).

Tracy wins again.

This is the win/lose map for the optimal play, you can create it from the winning square going backward. Since Charile is forced to play a bad move, Tracy will win if she plays optimally.

Oh, that Tracy, always happy to fool her poor friend Charlie. He needs to be wary of mathematically savvy trolls, it's for his own good.

Either way, the following picture contains the playing board with the following coloring pattern:

• Pink squares are "losing" squares (if the coin is in that square in the beginning your turn, then you lose).

• Blue squares are "winning" squares (if the coin is in that square in the beginning of your turn, then you win).

The coloring rule for this diagram is pretty simple:

• The upper left corner is always pink (if your opponent put the coin there, it's game over for you).

• Any square from which a pink square is reachable in one move is blue (that is, you can place the coin at a losing position for your opponent).

• Any square from which only blue squares are reachable is pink (that is, you can only place the coin at a winning position for your opponent).

With this simple rule, it is possible to color the whole board, and conclude that the game starts at a losing position for silly old Charlie . Maybe they should play something else? Looking forward to what these two will come up with next week!

Simple. Tracy only plays games which she can win.

Tracey, clearly. Why else would she propose the game?

25 is an odd number so add 1 and after Charlie is Tracy

Whoever goes in the green loses. Tracy can either easily make the coin go to the bottom left, middle left, top right, or top middle where she would ultimately win.