More Queue Positions
Some students, including Rohit and Pranshu, are standing in a line.
- Rohit is the 5th person in line counting from the right.
- Pranshu is the 5th person in line counting from the left.
- There are 3 people in the line between Pranshu and Rohit.
How many people are there in the line?

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
vERY GOOD :D
My only question was what "5th person in queue counting from the left/ right" fundamentally meant. I was thinking of it as that the 5th person from the right must be the person on the FAR right of the line, and vice versa with the left. So in theory (if we weren't given options) it could be anywhere from 5 to infinite people.
Log in to reply
Yes but there needs to be 3 people in between the two people, so if it was infinite amount of people in the line, then there would be infinite people in between the two people, it doesn't work.
Log in to reply
I disagree. My mind says that even if there is an infinite number of people, to answer this puzzle, as long as these 5 people stay in their designated formation, any where in the line, the answer is always the number of people in the line. So, an infinite number of people is, with no change in the formation, an infinite number of people!
Log in to reply
@Kay Bushnell – Counting "from the left" or "from the right" requires that you're counting from the left end or the right end, respectively, so there is a limit to the number of people who can be in the line outside of the five-person group that includes Rohit and Pranshu at either end.
The only portion where you could find vagueness would be in the statement, "there are three people between them". You could choose (incorrectly) to interpret that as "there are at least three people between them", or, as intended, "there are precisely three people between them", but you can't get away from their defined distances from the ends of the line.
I also did by the same method but you explained it well.
A queue is not counted from both sides.A queue is always in 1 direction.A queue has a beginning and an end.
Log in to reply
And where, exactly, lies the problem with observing a queue and seeking the person you're looking for while counting from the back of the queue instead of the front?
I also disagree with this answer/analysis. Definition of a queue: a line or sequence of people or vehicles awaiting their turn to be attended to or to proceed. In order to empty the queue, all of the members must be removed. If there are 13 people in line, you can't remove 5 of them and then say the queue is empty.
Unless you happen to work at the DMV, then that would be standard procedure. :)
Log in to reply
Where does it say in the problem statement that having 5 people get their turn and exit from the queue would empty the queue?
I love your diagrams and analysis. I am quite concerned with your conclusion "both 5 and 13". Consider the following: L(x) is the the statement "the line has x people". You claim the following L(5) AND L(13). We read this as "the line has 5 people and the line has 13 people". This statement is false, unless 5 = 13. Your conclusion should read "therefore, the answer is either 5 or 13". Essentially L(5) or L(13). As such, we are stating that as long as one of the statements is true, be it L(5) else L(13), then the whole statement "L(5) or L(13)" is true. Aside from this small logical snafu your write is flawless.
This is very wrong. The answer should be 13, a queue is linear. it could either be last in first out or first in first out. If 13 and 5 is arguable then it could happen that 1 - 13 could be the answer. Why? Think of multidimensional arrays, you can have a 2slot queue with each slot having multiple entities.
Log in to reply
But the problem isn't talking about things like first-in first-out though. And it is also irrelevant. Linearity of queues doesn't come into play either.
Another way of looking at the problem is this: counting from last-entered to first-entered, Pranshu was the fifth person to ENTER the queue (in other words, there were 4 people that entered the queue after Pranshu). Rohit, meanwhile, is currently fifth in line to EXIT the queue. There are 3 people in the queue standing in between Pranshu and Rohit. Notice, first of all, how we're talking about 3 people standing IN BETWEEN Pranshu and Rohit. There's nothing in the problem about whether those 3 people are standing BEHIND Pranshu (and thus in front of Rohit), or the other way around. The second thing to note, of course, is that the problem only states the two guys' position respective to the back and front of the queue respectively. This indicates exactly NOTHING about whether Pranshu is in front of Rohit, or Rohit is in front of Pranshu.
So, what's the answer then? Well, as "Hugo Posthuma" explained: either there are 13 people, with Rohit being 5th in line and Pranshu being 9th..... OR, there are 5 people, with Pranshu being 1st in line and Rohit being 5th (and last). Now, it shouldn't be all that hard to see that BOTH solutions work. Since you're having trouble with the "There are 5 people in the queue" solution, it would be most beneficial I feel to focus on that one. Well, the first requirement of the problem was that there were 4 people that entered the queue after Pranshu. If there are 5 people in the queue and Pranshu is 1st in line, then this clearly holds. That Rohit is one of those 5 people standing behind Pranshu in the queue doesn't contradict this requirement (especially since this first requirement doesn't even MENTION Rohit). Second requirement: Rohit is 5th in line. Clearly this is true in the 5-people-solution. The 2nd requirement says precisely nothing about Pranshu, so it is simply IMPOSSIBLE for Pranshu's position to have an effect on whether or not said requirement is met. The only requirement which concerns itself with Pranshu's and Rahit's relative position is the 3rd requirement. However, like mentioned before, the 3rd requirement is an entirely SYMMETRIC requirement -- or, in other words, it doesn't talk about the ORDER in which Pranshu and Rohit appear in the queue. It only talks about how many people are in between them.... but the phrase "in between" is itself an entirely symmetric term. The nature of a queue has no bearing on that whatsoever at all. Thus, we have EXHAUSTIVELY shown that not only the 13-person-solution, but also the 5-person-solution is a valid solution to the problem as presented.
It's a que, not a line. 13 is the correct answer.
Log in to reply
Excuse me, the answer (according to brilliant) was 5 and 13
I think they are the same thing. Can you explain me what the difference is?
You're thinking in terms of queue vs stack, instead of what the problem states, which is simply a group that happens to be arranged in a linear fashion. There's no direction or order given to the line, other than that it can be counted from either end. Therefore, 5 and 13 are both valid responses.
In fact, this is very true
But how can it be 5 OR 13? I am bewildered on how you could determine the answer to be 5 in any capacity; I only see how you could arrive at the answer of 13. Thank you for your explanation, but if someone could help me understand why you could have an answer of 5 I would appreciate that.
Log in to reply
Take a look at the first diagram. Rohit is the "fifth from the right" since there are four people to the right of him. Pranshu is "fifth from the left" since there are four people to the left of him. There are also exactly three people between Rohit and Pranshu. Therefore, 5 is a valid solution. The same logic can be used in the second diagram to show that 13 is a valid solution.
? People in line. Five from right. Five from left. That's ten! Three in the middle. That's 13 people in a line of people.
I liked the logic....
However all of this ignores the question of how many people are in THE line, Some students, including Rohit and Pranshu, are standing in a line.there positions are irrelevant in this question as it is a single line containing 13 people. so the answer is incorrect
Log in to reply
The point of the problem is that you don't know how many people are in the line, and from the information given, it could either be 5 or 13. The descriptions of their positions are integral to solving the problem, precisely because we're not told how many people are in the line.
Relevant wiki: Linear Equations - Problem Solving
There are 2 possible answers, depending on whether Pranshu or Rohit is standing in front of the other one. We can easily find these solutions as 5 or 13, just by thinking about it.
Here is an algebraic approach:
Let there be n people in the queue.
Rohit = n − 4 (5th from the back)
Pranshu = 5
Case 1: Pranshu is in front of Rohit
( n − 4 ) = 4 + ( 5 ) (The four signifies 3 places in between them)
n = 1 3
Case 2: Rohit is in front of Pranshu
( 5 ) = 4 + ( n − 4 )
n = 5
Actually, an easier way to find one answer is to just count how many people there are in the diagram
Log in to reply
I answered this problem before there was a diagram included in the question.
We are told that one person is 5th in line from the right and another person is 5th in line from the left with three more indevidules between those two indicating there is a limit to the total amount of people in the cue. The total amount being 13, which answers the question. I think there is only one answer to this problem. The question asks “how many” people and the answer is 13.
The question clearly asks, how many people? The answer is 13. I don't know how I got this wrong. I counted the people in line and there are 13 people. How is this wrong? I would rate this problem a 5 because it was confusing but it was simple to do so it's in the middle. I was very confused because to find the total number of people, counting them is the easiest way.
Log in to reply
I answered this problem before there was a diagram, hence the algebraic approach. Also, if you choose to look at the diagram, you can also see that 5 people are coloured in.
-
Let n be number of people in queue.
-
Prashnu is 5 th from the left .
-
Rohit is 5 from the right ⟹ Rohit is ( n − 5 + 1 ) = ( n − 4 ) th from the left .
-
So, number of people between Rohit and Prashnu is ∣ ( n − 4 ) − 5 ∣ − 1 = ∣ n − 9 ∣ − 1 . A great food for thought is: why is the number of people NOT ∣ ( n − 4 ) − 5 − 1 ∣ ?
-
But, we have, ∣ n − 9 ∣ − 1 = 3 ⟹ ∣ n − 9 ∣ = 4 ⟹ n = 5 , 1 3 .
Excellent but complicated.
Both are correct, I think if we want only a correct answer, we should add in the question something like..."with the lesser number of people"
Log in to reply
That's not correct, only 5 is correct.
Log in to reply
How is only 5 correct? A line of 5 people matches the criteria of the problem, and a line of 13 people matches the same criteria.
Log in to reply
@Brian Egedy – Exactly Brian C:, Jack you are interpreting the diagram like you want :C
This isn't a modernized queue, if this was a video game lobby the correct answer is 5.
Log in to reply
The correct answer is 5. The reason it is correct is because the instructions specifically said: "based on the information given".
The given information stated one individual was five from the left the other five from the right with three people in between. It never mentioned anything about the other eight people.
Log in to reply
Start with a line of 13 people. Choose the person that is five from one end of the line, and then choose a second person, who is five from the other end. There will be three people between them. That setup meets the criteria given in the problem, therefore this is a valid answer to the question. The question never states that there are only three other people in the line.
Diagram is misleading
Log in to reply
The diagram is does not need to be accurate. If it's accurate, then it's better to just rephrase the question to "Look at this picture, tell me what do you see?"
The problem needs to explicitly state that the line of people shown below is part of the problem. Otherwise one has to assume, and we all know how that often turns out.
Log in to reply
The diagram is not necessary to solve the problem. It is only included as a visual aid and to hint that there may be more than one solution.
I thought of them 5 being in a circle ⭕️. Another alternate of solution to the answer 5.
It makes more sense to me if I could think the queue as a circle = 5 and a straight line = 13, Thanks.
That is another interesting way to look at it.
all these stupid questions are trick questions...either work on real knowledge or quit playing around with riddles. riddles don't display intelligence.
These are problems in the easy section. If you want to see some harder problems, I'd urge you to go to the hard section and check out the problems there.
the issue is that they draw the actual line of people. How can I think anything else if it shows me it
Log in to reply
The image is an example of counting "five from the right" for people in a line. The problem says nothing about the image being "the line" of the problem.
Riddles display comprehension and flexibility of thinking. The fact that a question is tricky doesn't make it worthless, it just makes it an exercise in more than one type of thinking.
How is this a riddle? The answer must be 5 or 13.
We have all the information we need to solve this problem. A possibility of this answer could look something like this.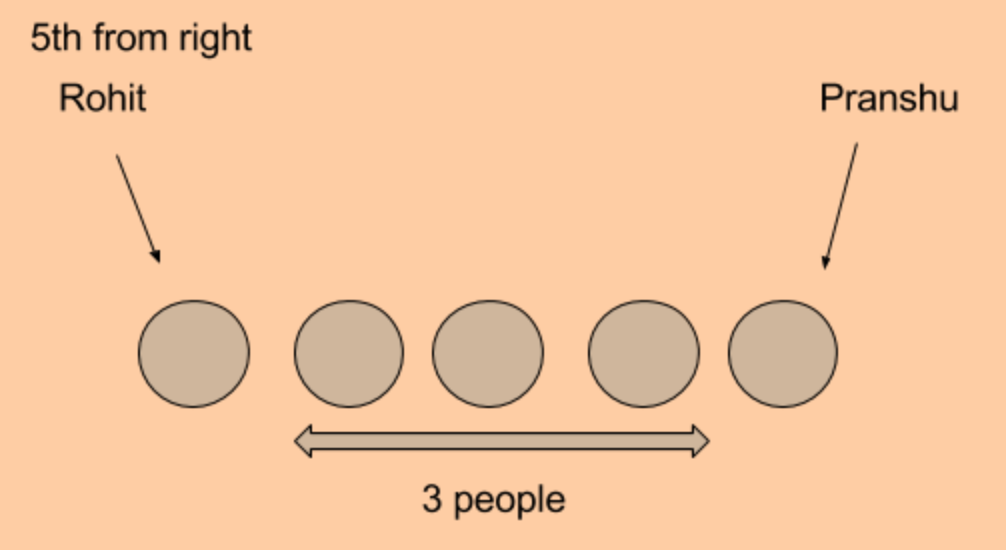
However, it can also look like this. Being instead of 5 people, we can have 13.
It satisfies all the required conditions, therefore, the answer is both 5 and 13.