A drifting boat
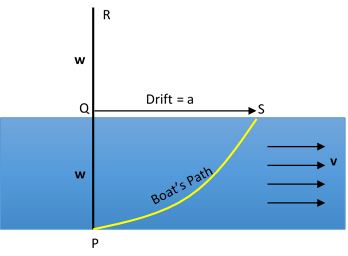
A river is flowing at a uniform velocity of v = 1 0 m/s . As shown in the diagram, P , Q , and R are three points on a line perpendicular to the river such that P Q = Q R = 1 0 0 m .
A boat starts from point P and moves at a constant speed of v = 1 0 m/s relative to the river. It moves in such a way that the direction of its resultant velocity is always perpendicular to the line joining the boat and point R .
If the boat drifts a meters and takes b seconds to land on point S , submit your answer as a + b to 3 decimal places.
P.S If you liked this problem, check this one out too!!!
The answer is 186.375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 Very happy to solve this awsome problem,
Very happy to solve this awsome problem,
Awesome!!....Hua nhi mjhse😂
Did it the same way. At first, I guessed the trajectory to be a circle, and immediately concluded it to be 2 0 0 , but even after getting the right solution, I wanted to prove it!
Same here too!
Since the resultant velocity is always perpendicular to the line joining the boat and R , the boat is moving in a circle of radius 2 w .
1) Thus the drift will be Q S = 4 w 2 − w 2 = 3 w
2) Suppose at any arbitrary time, the boat is at point B .
V n e t = 2 v cos θ
d t d θ = 2 w V n e t = w v cos θ
Cross multiplying :-
v w sec θ d θ = d t
Now integrating and using proper limits(at time t = 0 , the line joining R and P makes an angle of 0 ∘ , and at time t , the angle becomes 6 0 ∘ )
∫ 0 t d θ = v w ∫ 0 6 0 ∘ sec θ d θ
t = v w [ l n ( sec θ + tan θ ) ] 0 6 0 ∘
t = v 1 . 3 1 7 w
So adding them we get :-
[ ( 1 . 3 1 7 ) ( 1 0 ) + 3 ] ( 1 0 0 )
= 1 8 6 . 3 7 5
P.S If someone could pls help me with this solution by providing an image, it would be really great as it may prove to be difficult to deduce what angle is θ and some of the other things too.
ok will image in paint will be fine??
Log in to reply
Yup.All I need is an image which labels all the points and angles mentioned in my solution.Thank you
Log in to reply
ok when ever i get free time i will make it
Log in to reply
@Nivedit Jain – Thanks. I do hope there was a better way........
Log in to reply
@Pranav Saxena – which way is in your mind?? PLzzz share
Log in to reply
@Nivedit Jain – A better way so as to make images. Paint seems tiresome......... and making them in word and then converting them to jpg is also a lot of work.........
@Pranav Saxena Why have you taken θ as 60°?
Log in to reply
.When the boat reaches the opposite shore, it forms an equilateral triangle with the point R.Its difficult to convey this without an image..