Motocross Front Flip

In 2011, Jackson Strong won the gold medal for freestyle motocross best trick at the summer X Games for a front flip over a sixty foot gap, the first in competition. Powering a dirt bike through a front flip is no easy task and requires an incredible combination of balance, strategic shifting of body weight, and... pulling the brakes. Let's explore the role of the brakes in facilitating the front flip.
We model model a dirt bike as a rod of mass and length to which are attached two wheels of mass and radius The bike goes off a spine ramp with angle to the vertical on either side (see diagram below).
Our question is, at what time, (in seconds), after leaving the ramp, should the rider pull the brakes (stopping both wheels instantaneously) if they want to do a front flip with minimum takeoff speed?
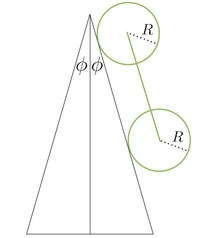
Details and assumptions
- Upon landing, the bike is parallel to the landing ramp, both wheels are in contact with the landing surface, and the back wheel contacts the very top of the ramp.
- The wheels are rings, i.e. the spokes are massless and all the mass is concentrated at the radius and .
- Assume both wheels lose contact with the ramp at the same angular velocity, , where is the velocity of the motorcycle upon losing contact with the ramp.
- The bike coasts off the ramp, i.e. there is no power from the engine putting a torque on the wheel.
The answer is 1.57715.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The first thing to realize is the the center of mass of the dirt bike travels like a point particle for the entirety of the flip. We should therefore calculate the initial and final locations of the center of mass according to the conditions in the assumptions, which will allow us to calculate the minimum velocity, and the hang time of the jump.
We are told that the bike coasts off the ramp, which means that that when the bike loses contact with the ramp, it looks like this:
from which we can write the x and y coordinates of the center of mass as
y c o m i n i x c o m i n i = R sin ϕ + 2 L sin ( 2 π − ϕ ) = R cos ϕ − 2 L cos ( 2 π − ϕ )
Now, we say that we want to take off with the minimum speed. This means that the landing configuration will be as is shown below, with the back wheel just clearing the lip of the spine:
From this, we can write the center of mass upon landing as:
y c o m f i n x c o m f i n = R sin ϕ − 2 L sin ( 2 π − ϕ ) = − R cos ϕ − 2 L cos ( 2 π − ϕ )
With this bookkeeping out of the way, the trajectory of the center of mass is pretty boring:
x c o m f i n y c o m f i n = x c o m i n i − v 0 t a i r sin ϕ = y c o m i n i + v 0 t a i r cos ϕ − 2 1 g t a i r 2
Solving these relations tells us the initial velocity v 0 as well as the air time t a i r .
v 0 = sin ϕ ( L sin ϕ + 2 R cos ϕ ) g R L sin 2 ϕ + 2 R cos 2 ϕ + 2 R t a i r = g sin ϕ L sin 2 ϕ + 4 R cos 2 ϕ
The interesting part of the problem comes from the angular momentum and makes use of a convenient way of writing the angular momentum for a system of particles.
Initially, the only angular momentum in the system is in the wheels, from the spinning of the tires about their center. The moment of inertia for each tire is given by m R 2 and each tire spins with the angular speed ω 0 = v 0 / R , so that L i n i = 2 m R 2 ω = 2 m R v 0
Now, let's consider a system of particles with center of mass r c o m , positions r 1 , r 2 , … , r n relative to the center of mass, and velocities v 1 , v 2 , … , v n . Their angular momentum with respect to the origin can be written as
L = i ∑ r i ′ × p i = i ∑ m i ( r i + r c o m ) × v i = i ∑ m i r i × v i + i ∑ m i r c o m × v i = L c o m p a r t i c l e s + L o r i g i n c o m
which shows that the angular momentum of a system of particles is, plainly, the angular momentum of the particles about their center of mass plus the angular momentum of their center of mass about the origin of the coordinate system.
With this result, we can easily calculate the angular momentum of the dirt bike wheels about the center of mass of the dirt bike. We know that before the brakes are pulled, the angular momentum of each wheel's center of mass about the center of mass of the dirt bike is zero, therefore, the angular momentum about the center of mass of the dirt bike is simply given by the angular momentum of the wheel's rotational motions, i.e. L c o m = 2 m R v 0 .
Once the brakes are pulled, the wheels are no longer spinning and therefore, no longer carry any angular momentum from spinning. However, the angular momentum about the center of mass of the dirt bike is conserved, and must manifest somehow. The only other motion available to the system is the for the entire dirt bike to spin about its center of mass, which is what happens. As long as the wheels carry enough angular momentum to rotate the bike through 5 3 8 ∘ in less than t a i r seconds, the rider will be able to do a front flip using the brakes alone.
We can calculate the moment of inertia for the dirt bike about its center of mass as follows. The rod has a moment of inertia of 1 2 1 M L 2 . Each wheel can be calculated using the parallel axis theorem, i.e. I w h e e l = m R 2 + m 4 L 2 so that the moment of inertia of the dirt bike is given by
I b i k e = 1 2 1 M L 2 + 2 m R 2 + 2 1 m L 2
Now, from the trajectory, we know that the bike has t a i r seconds in the air before touching down on the landing ramp. In this time, the bike must rotate 5 4 0 ∘ − 2 ∘ = 5 3 8 ∘ . If we pull the brakes at time t p u l l , we'll have t a i r − t p u l l seconds to complete the rotation. In other words we have
ω t = 5 3 8 ∘ 1 8 0 ∘ π = I b i k e L c o m ( t a i r − t p u l l ) = ω b i k e ( t a i r − t p u l l ) = π 9 0 2 6 9
Note : if we pull the brakes before t p u l l , the bike will over rotate and we'll screw up the trick (in reality there is a good deal of leeway, but we are trying to be perfect).
Writing this out, we have
ω b i k e = I b i k e L c o m = L 2 ( 6 m + M ) + 2 4 m R 2 2 4 m R v 0
Putting it all together, we have:
L 2 ( 6 m + M ) + 2 4 m R 2 2 4 m R v 0 ( g sin ϕ L sin 2 ϕ + 4 R cos 2 ϕ − t p u l l ) = π 9 0 2 6 9
Using the figures provided in the problem, we find v 0 ≈ 1 6 . 5 m/s , t a i r ≈ 3 . 4 8 s , and t p u l l ≈ 1 . 5 8 s .
At, t p u l l , the bike will be at 1 4 . 7 9 m above the spine ramp, just before its peak at 1 4 . 8 5 m . This leaves ( t a i r − t p u l l ) ≈ ( 3 . 4 8 − 1 . 5 8 ) s = 1 . 9 0 s , or a little more than half the air time for the front flip.